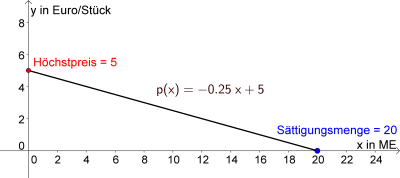Kosten- und Preistheorie: Unterschied zwischen den Versionen
(→Erlösfunktion) |
|||
| (27 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | Die folgenden zwei Videos zeigen geben dir eine Zusammenfassung aller wichtigen Punkte der Kosten- und Preistheorie. Details zu den einzelnen Begriffen findest du unterhalb der Videos. | |
| − | + | {| class="wikitable" | |
| + | |- | ||
| + | ! Auflistung aller wichtigen Begriffe | ||
| + | ! Beispiel | ||
| + | |- | ||
| + | | {{Vorlage:Video|1=70Hm5VW1I3s}} | ||
| + | | {{Vorlage:Video|1=InBC4XO5Ex8}} | ||
| + | |} | ||
| + | |||
== Preisfunktion der Nachfrage == | == Preisfunktion der Nachfrage == | ||
| Zeile 64: | Zeile 72: | ||
}} | }} | ||
| − | {{Vorlage:Beispiel|1= Gegeben ist die Preisfunktion $p$ mit $p(x)=-0.25x+5$ | + | {{Vorlage:Beispiel|1= Gegeben ist die Preisfunktion $p$ mit $p(x)=-0.25x+5$. |
| + | <br> | ||
| + | <br> | ||
* Stellen Sie die dazugehörige Erlösfunktion auf. | * Stellen Sie die dazugehörige Erlösfunktion auf. | ||
* Bestimmen Sie die sogenannten Erlösgrenzen, dies sind die [[Nullstelle|Nullstellen]] der Erlösfunktion. | * Bestimmen Sie die sogenannten Erlösgrenzen, dies sind die [[Nullstelle|Nullstellen]] der Erlösfunktion. | ||
| Zeile 79: | Zeile 89: | ||
$$0=-0.25x^2+5x$$ | $$0=-0.25x^2+5x$$ | ||
Durch herausheben von $x$, [[Quadkom]] oder den [[Löse-Befehl]] erhalten wir $x_1=0$ und $x_2=20$. | Durch herausheben von $x$, [[Quadkom]] oder den [[Löse-Befehl]] erhalten wir $x_1=0$ und $x_2=20$. | ||
| + | |||
| + | <br> | ||
* Nun bestimmen wir den maximalen Erlös: | * Nun bestimmen wir den maximalen Erlös: | ||
| + | <br> | ||
'''1. Variante:''' Mithilfe der Eigenschaften einer quadratischen Funktion. | '''1. Variante:''' Mithilfe der Eigenschaften einer quadratischen Funktion. | ||
| Zeile 100: | Zeile 113: | ||
=== Grenzerlös === | === Grenzerlös === | ||
[[Datei:Grenzerlös.png|300px|mini|rechts|Graph der Erlösfunktion mit graphischer Bestimmung des Grenzerlöses]] | [[Datei:Grenzerlös.png|300px|mini|rechts|Graph der Erlösfunktion mit graphischer Bestimmung des Grenzerlöses]] | ||
| − | {{Vorlage:Definition|1= Der | + | {{Vorlage:Definition|1= Der Grenzerlös $E'(x)$ gibt die (ungefähre) Zunahme/Abnahme des Erlöses an, wenn eine weitere Mengeneinheit produziert wird. |
| − | $ | + | |
| − | gibt die (ungefähre) Zunahme/Abnahme des Erlöses an, wenn eine weitere Mengeneinheit produziert wird. | + | |
}} | }} | ||
| Zeile 109: | Zeile 120: | ||
{{Vorlage:Beispiel|1= | {{Vorlage:Beispiel|1= | ||
| − | *Bestimmen Sie den Grenzerlös der Erlösfunktion $E$ mit | + | * Bestimmen Sie den Grenzerlös der Erlösfunktion $E$ mit $E(x)=-0.25x^2+5x$ bei einer Menge von $x=5$ ME und interpretieren Sie das Ergebnis. |
| − | + | ||
|2= | |2= | ||
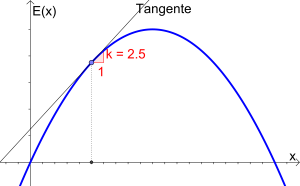
[[Datei:Grenzerlös-Bsp.png|300px|mini|rechts|Bestimmen des Grenzerlöses]]$$E'(x)=-0.5x+5$$ | [[Datei:Grenzerlös-Bsp.png|300px|mini|rechts|Bestimmen des Grenzerlöses]]$$E'(x)=-0.5x+5$$ | ||
| Zeile 116: | Zeile 126: | ||
$$E'(5)=2.5 \textrm{ GE pro Mengeneinheit}$$ | $$E'(5)=2.5 \textrm{ GE pro Mengeneinheit}$$ | ||
| − | Produziert man statt fünf Mengeneinheiten noch eine zusätzliche sechste, so steigt der Erlös (ungefähr) um $2.5$ Geldeinheiten. | + | '''Interpretation:''' Produziert man statt fünf Mengeneinheiten noch eine zusätzliche sechste, so steigt der Erlös (ungefähr) um $2.5$ Geldeinheiten. |
<br> | <br> | ||
| Zeile 127: | Zeile 137: | ||
{{Vorlage:Hinweis|1=Das „ungefähr“ wird deshalb verwendet, da die Tangente die Erlösfunktion nur bei $x=5$ berührt und somit bei $x=6$ ein leicht zu großer Wert herauskommt. | {{Vorlage:Hinweis|1=Das „ungefähr“ wird deshalb verwendet, da die Tangente die Erlösfunktion nur bei $x=5$ berührt und somit bei $x=6$ ein leicht zu großer Wert herauskommt. | ||
[[Datei:Grenzerlös-Unterschied-gif.gif|300px|mini|zentriert|Der Grenzerlös ist nur eine Näherung an die tatsächliche Steigung der Erlösfunktion.]]}} | [[Datei:Grenzerlös-Unterschied-gif.gif|300px|mini|zentriert|Der Grenzerlös ist nur eine Näherung an die tatsächliche Steigung der Erlösfunktion.]]}} | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
== Kostenfunktion == | == Kostenfunktion == | ||
=== Definition und Aufbau der Kostenfunktion === | === Definition und Aufbau der Kostenfunktion === | ||
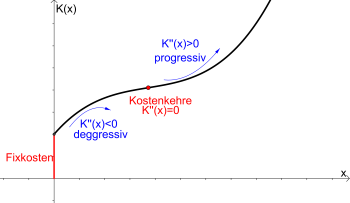
| − | [[Datei:Kostenfunktion-allgemein.png|350px|mini|right|Graph einer | + | [[Datei:Kostenfunktion-allgemein.png|350px|mini|right|Graph einer „ertragsgesetzlichen“ Kostenfunktion]] |
| − | {{Vorlage:Definition|1= Die Gesamtkosten für die Produktion werden durch die Kostenfunktion K angegeben. Die Kostenfunktion besteht dabei aus 2 Termen: | + | {{Vorlage:Definition|1= Die Gesamtkosten für die Produktion werden durch die Kostenfunktion $K$ angegeben. Die Kostenfunktion besteht dabei aus $2$ Termen: |
$$K(x)=K_v (x)+F$$ | $$K(x)=K_v (x)+F$$ | ||
| − | $K_v (x)...$ variable Kosten (jene Kosten, die von der produzierten Menge x abhängig sind) | + | $K_v (x)...$ variable Kosten (jene Kosten, die von der produzierten Menge $x$ abhängig sind) |
| − | $F...$ Fixkosten, die auch bei einer Produktion von 0 ME anfallen. | + | $F...$ Fixkosten, die auch bei einer Produktion von $0$ ME anfallen. |
}} | }} | ||
| Zeile 143: | Zeile 156: | ||
{{Vorlage:Merke|1=Typische Eigenschaften einer "ertragsgesetzlichen Kostenfunktion" | {{Vorlage:Merke|1=Typische Eigenschaften einer "ertragsgesetzlichen Kostenfunktion" | ||
*Eine Kostenfunktion heißt ertragsgesetzlich, wenn sie | *Eine Kostenfunktion heißt ertragsgesetzlich, wenn sie | ||
| − | ** streng monoton steigend ist (d.h. $K'(x)>0$ für alle $x$ im [[Definitionsbereich]]), | + | ** streng monoton steigend ist (d. h. $K'(x)>0$ für alle $x$ im [[Definitionsbereich]]), |
| − | ** zuerst einen degressiven Verlauf hat (d.h. rechtsgekrümmt, $K''(x)<0$) und | + | ** zuerst einen degressiven Verlauf hat (d. h. rechtsgekrümmt ist, sprich $K''(x)<0$) und |
| − | ** nach der Kostenkehre (Wendepunkt der Kostenfunktion, $K''(x)=0$) | + | ** nach der Kostenkehre (Wendepunkt der Kostenfunktion, sprich $K''(x)=0$) |
| − | ** einen progressiven Verlauf hat (d.h. linksgekrümmt, $K''(x)>0$). | + | ** einen progressiven Verlauf hat (d. h. linksgekrümmt ist, sprich $K''(x)>0$). |
}} | }} | ||
| Zeile 157: | Zeile 170: | ||
a) Bestimmen Sie die Fixkosten und die variablen Kosten der Funktion. | a) Bestimmen Sie die Fixkosten und die variablen Kosten der Funktion. | ||
| − | + | <br> | |
| − | b) Berechnen Sie die Kosten bei einer Produktion von 12 ME. Geben Sie auch an, wie hoch die variablen Kosten sind. | + | b) Berechnen Sie die Kosten bei einer Produktion von $12$ ME. Geben Sie auch an, wie hoch die variablen Kosten sind. |
| − | + | <br> | |
| − | c) Ermitteln Sie die Produktionsmenge, wenn Kosten von 60 GE anfallen. | + | c) Ermitteln Sie die Produktionsmenge, wenn Kosten von $60$ GE anfallen. |
|2= | |2= | ||
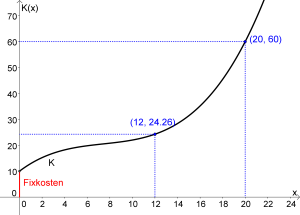
| − | [[Datei:Kostenfunktion-Bsp1.png|300px|mini|rechts|Graph der Kostenfunktion K]] | + | [[Datei:Kostenfunktion-Bsp1.png|300px|mini|rechts|Graph der Kostenfunktion $K$]] |
| − | a) Die Kostenfunktion lautet $K(x)=0.017x^3−0.38x^2+3.3x+10$. Der konstante Term gibt die Fixkosten an, der Term mit den x gibt die variablen Kosten an: | + | a) Die Kostenfunktion lautet $K(x)=0.017x^3−0.38x^2+3.3x+10$. Der konstante Term gibt die Fixkosten an, der Term mit den $x$ gibt die variablen Kosten an: |
* Fixkosten: $10$ | * Fixkosten: $10$ | ||
* Variable Kosten: $0.017x^3−0.38x^2+3.3x$ | * Variable Kosten: $0.017x^3−0.38x^2+3.3x$ | ||
| + | <br> | ||
b) Gefragt sind die Kosten bei $x=12$ ME und gesucht ist $K(12)$: | b) Gefragt sind die Kosten bei $x=12$ ME und gesucht ist $K(12)$: | ||
$$K(12)=0.017\cdot 12 ^3−0.38 \cdot 12^2+3.3\cdot 12+10=24.256 \textrm{ GE}$$ | $$K(12)=0.017\cdot 12 ^3−0.38 \cdot 12^2+3.3\cdot 12+10=24.256 \textrm{ GE}$$ | ||
| + | <br> | ||
| − | c) Die Kosten betragen $K(x)=60$ und gesucht ist x: | + | c) Die Kosten betragen $K(x)=60$ und gesucht ist $x$: |
$$60=0.017x^3−0.38x^2+3.3x+10$$ | $$60=0.017x^3−0.38x^2+3.3x+10$$ | ||
Mithilfe von Technologie (siehe [[TI-Befehle]] bzw. [[GeoGebra]]) erhalten wir: | Mithilfe von Technologie (siehe [[TI-Befehle]] bzw. [[GeoGebra]]) erhalten wir: | ||
$$x=20$$ | $$x=20$$ | ||
| − | A: Bei einer Produktion von 20 ME fallen Kosten von 60 GE an. | + | A: Bei einer Produktion von $20$ ME fallen Kosten von $60$ GE an. |
| Zeile 181: | Zeile 196: | ||
=== Grenzkosten === | === Grenzkosten === | ||
| − | {{Vorlage:Definition|1= Die $ | + | {{Vorlage:Definition|1= Die Grenzkosten $K'(x)$ geben die (ungefähre) Zunahme/Abnahme der Kosten an, wenn eine weitere Mengeneinheit produziert wird. $K'(x)$ bezeichnet dabei die [[Ableitung bestimmen|1. Ableitung]] von $K(x)$. |
| − | geben die (ungefähre) | + | |
}} | }} | ||
Bild mit Tangente und Steigungsdreieck | Bild mit Tangente und Steigungsdreieck | ||
| Zeile 188: | Zeile 202: | ||
{{Vorlage:Beispiel|1= Gegeben ist die Kostenfunktion | {{Vorlage:Beispiel|1= Gegeben ist die Kostenfunktion | ||
$$K(x)=0.017x^3−0.38x^2+3.3x+10$$ | $$K(x)=0.017x^3−0.38x^2+3.3x+10$$ | ||
| − | * Bestimmen Sie die Grenzkosten bei einer Produktionsmenge von 20 ME. | + | * Bestimmen Sie die Grenzkosten bei einer Produktionsmenge von $20$ ME. <br> |
| − | + | ||
* Interpretieren Sie das Ergebnis. | * Interpretieren Sie das Ergebnis. | ||
| + | |||
|2= | |2= | ||
Die Grenzkosten ermitteln wir mithilfe der [[Ableitung bestimmen|ersten Ableitung]]: | Die Grenzkosten ermitteln wir mithilfe der [[Ableitung bestimmen|ersten Ableitung]]: | ||
$$K(x)=0.017x^3−0.38x^2+3.3x+10$$ | $$K(x)=0.017x^3−0.38x^2+3.3x+10$$ | ||
$$K'(x)=0.051x^2-0.76x+3.3$$ | $$K'(x)=0.051x^2-0.76x+3.3$$ | ||
| − | $K'(x)$ gibt uns die | + | $K'(x)$ gibt uns die Grenzkostenfunktion an. Nun müssen wir nur noch die Grenzkosten bei $20$ ME, d. h. $K'(20)$ bestimmen: |
$$K'(20)=0.051\cdot 20^2-0.76\cdot 20+3.3$$ | $$K'(20)=0.051\cdot 20^2-0.76\cdot 20+3.3$$ | ||
$$K'(20)=8.5\textrm{ GE/ME} $$ | $$K'(20)=8.5\textrm{ GE/ME} $$ | ||
| − | Die Grenzkosten bei einer Produktionsmenge von $x=20$ ME betragen 8.5 GE/ME. | + | Die Grenzkosten bei einer Produktionsmenge von $x=20$ ME betragen $8.5$ GE/ME. |
| − | Interpretation: Bei einer Produktion von 20 Mengeneinheiten fallen für eine zusätzlich produzierte 21. Mengeneinheit Kosten von ca. 8.5 | + | '''Interpretation:''' Bei einer Produktion von $20$ Mengeneinheiten fallen für eine zusätzlich produzierte $21$. Mengeneinheit Kosten von ca. $8.5$ GE/ME an. |
}} | }} | ||
=== Stückkostenfunktion, Betriebsoptimum und langfristige Preisuntergrenze === | === Stückkostenfunktion, Betriebsoptimum und langfristige Preisuntergrenze === | ||
| − | {{Vorlage:Definition|1= Die Stückkosten $\bar{K}(x)$ geben die durchschnittlichen Kosten pro Stück (oder Mengeneinheit) an und berechnen sich, indem die Gesamtkosten durch die | + | {{Vorlage:Definition|1= Die Stückkosten $\bar{K}(x)$ geben die durchschnittlichen Kosten pro Stück (oder Mengeneinheit) an und berechnen sich, indem die Gesamtkosten durch die Stückzahlen dividiert werden, d. h. mit |
$$\bar{K}(x)=\frac{K(x)}{x}$$ | $$\bar{K}(x)=\frac{K(x)}{x}$$ | ||
| − | $x...$ Anzahl der produzierten | + | $x...$ Anzahl der produzierten Stückzahlen (oder Mengeneinheiten). |
$K(x)...$ Gesamtkosten | $K(x)...$ Gesamtkosten | ||
| Zeile 219: | Zeile 233: | ||
... ist jene Stelle, bei der die Stückkosten $\bar{K}(x)$ ein Minimum (Tiefpunkt) haben. | ... ist jene Stelle, bei der die Stückkosten $\bar{K}(x)$ ein Minimum (Tiefpunkt) haben. | ||
| − | Die dazugehörigen Stückkosten $\bar{K}(x_{opt})$ nennt man '''langfristige Preisuntergrenze''' (oder auch '''kostendeckender Preis''')}} | + | Die dazugehörigen Stückkosten $\bar{K}(x_{opt})$ nennt man '''langfristige Preisuntergrenze''' (oder auch '''kostendeckender Preis''').}} |
{{Vorlage:Video|1=WOPQ3bYv4Ak}} | {{Vorlage:Video|1=WOPQ3bYv4Ak}} | ||
| Zeile 228: | Zeile 242: | ||
$$K(x)=0.017x^3 - 0.38x^2 + 3.3x + 10$$ | $$K(x)=0.017x^3 - 0.38x^2 + 3.3x + 10$$ | ||
| − | * Berechnen Sie das Betriebsoptimum und die langfristige Preisuntergrenze | + | * Berechnen Sie das Betriebsoptimum und die langfristige Preisuntergrenze. |
|2= Zuerst bestimmen wir die Stückkostenfunktion: | |2= Zuerst bestimmen wir die Stückkostenfunktion: | ||
| Zeile 238: | Zeile 252: | ||
Nun berechnen wir das Minimum der Stückkostenfunktion. Entweder mit dem Minimumbefehl ([[TI-Befehle]],[[GeoGebra]]) oder (wie hier) mithilfe der Differentialrechnung (siehe [[Ableitung bestimmen]] bzw. [[Extremstellen|Kurvendiskussionen]]): | Nun berechnen wir das Minimum der Stückkostenfunktion. Entweder mit dem Minimumbefehl ([[TI-Befehle]],[[GeoGebra]]) oder (wie hier) mithilfe der Differentialrechnung (siehe [[Ableitung bestimmen]] bzw. [[Extremstellen|Kurvendiskussionen]]): | ||
[[Datei:Betriebsoptimum-Bsp.png|300px|mini|rechts|Graph der Stückkostenfunktion]] | [[Datei:Betriebsoptimum-Bsp.png|300px|mini|rechts|Graph der Stückkostenfunktion]] | ||
| − | Um das Minimum zu berechnen, ermitteln wir zuerst $\bar{K}'(x)$ und setzen dies dann 0: | + | Um das Minimum zu berechnen, ermitteln wir zuerst $\bar{K}'(x)$ und setzen dies dann gleich $0$: |
$$\bar{K}'(x)=0.034x - 0.38 -10x^{-2}$$ | $$\bar{K}'(x)=0.034x - 0.38 -10x^{-2}$$ | ||
$$0=0.034x - 0.38 -10x^{-2}\ \ \ \ \vert \cdot x^2$$ | $$0=0.034x - 0.38 -10x^{-2}\ \ \ \ \vert \cdot x^2$$ | ||
| Zeile 245: | Zeile 259: | ||
$$x_{opt}=12.93$$ | $$x_{opt}=12.93$$ | ||
| − | Antwort: Das Betriebsoptimum liegt bei 12.93 Mengeneinheiten. | + | Antwort: Das Betriebsoptimum liegt bei $12.93$ Mengeneinheiten. |
| − | Die dazugehörenden Stückkosten, die sogenannte langfristige Preisuntergrenze | + | Die dazugehörenden Stückkosten, die sogenannte langfristige Preisuntergrenze, liegen bei: |
$$\bar{K}(x_{opt})=\bar{K}(12.93)= 2 \textrm{ GE pro ME}$$ | $$\bar{K}(x_{opt})=\bar{K}(12.93)= 2 \textrm{ GE pro ME}$$ | ||
}} | }} | ||
| Zeile 280: | Zeile 294: | ||
$$\bar{K_v}'(x)=0.034x-0.38$$ | $$\bar{K_v}'(x)=0.034x-0.38$$ | ||
$$0=0.034x-0.38\ \rightarrow \underline{\underline{x_{min}= 11.18} }$$ | $$0=0.034x-0.38\ \rightarrow \underline{\underline{x_{min}= 11.18} }$$ | ||
| − | Das Betriebsminimum liegt somit bei 11.18 Mengeneinheiten. | + | Das Betriebsminimum liegt somit bei $11.18$ Mengeneinheiten. |
Zuletzt berechnen wir noch die kurzfristige Preisuntergrenze $\bar{K_v}(x_{min})$: | Zuletzt berechnen wir noch die kurzfristige Preisuntergrenze $\bar{K_v}(x_{min})$: | ||
| Zeile 286: | Zeile 300: | ||
$$\bar{K_v}(11.18)=0.017\cdot 11.18^2−0.38\cdot 11.18+3.3$$ | $$\bar{K_v}(11.18)=0.017\cdot 11.18^2−0.38\cdot 11.18+3.3$$ | ||
$$\underline{\underline{\bar{K_v}(x)=1.18} }$$ | $$\underline{\underline{\bar{K_v}(x)=1.18} }$$ | ||
| − | Die kurzfristige Preisuntergrenze beträgt somit 1.18 GE und wird erreicht, wenn $x_{min}= | + | Die kurzfristige Preisuntergrenze beträgt somit $1.18$ GE und wird erreicht, wenn $x_{min}=11.18$ ME produziert werden. |
}} | }} | ||
| Zeile 293: | Zeile 307: | ||
=== Allgemein === | === Allgemein === | ||
Mithilfe des Erlöses (Umsatz) und der Kosten können wir nun den Gewinn berechnen: | Mithilfe des Erlöses (Umsatz) und der Kosten können wir nun den Gewinn berechnen: | ||
| − | [[Datei: | + | [[Datei:Gewinnfunktion.png|300px|mini|rechts|Gewinnanalyse]] |
| − | {{Vorlage:Definition|1= Sei x die Menge der produzierten und zugleich verkauften Mengeneinheiten, dann erhält man den Gewinn G aus | + | {{Vorlage:Definition|1= Sei $x$ die Menge der produzierten und zugleich verkauften Mengeneinheiten, dann erhält man den Gewinn $G$ aus |
$$G(x)=E(x)-K(x)$$ | $$G(x)=E(x)-K(x)$$ | ||
Der Gewinn ergibt sich, wenn man vom Erlös die Kosten abzieht. | Der Gewinn ergibt sich, wenn man vom Erlös die Kosten abzieht. | ||
| Zeile 301: | Zeile 315: | ||
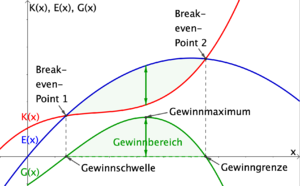
Folgende Punkte sind bei der Analyse der Gewinnfunktion relevant: | Folgende Punkte sind bei der Analyse der Gewinnfunktion relevant: | ||
{{Vorlage:Merke|1= $ $ | {{Vorlage:Merke|1= $ $ | ||
| − | * Der '''Break-even-Point''' ist jener Punkt, bei dem der Gewinn das erste Mal nicht mehr negativ ist (=1. [[Nullstelle]] der Gewinnfunktion). | + | * Der '''Break-even-Point''' ist jener Punkt, bei dem der Gewinn das erste Mal nicht mehr negativ ist (= 1. [[Nullstelle]] der Gewinnfunktion). |
* Der '''Gewinnbereich''' (auch Gewinnzone genannt) ist jenes Intervall, bei dem der Gewinn $G(x)>0$ ist. | * Der '''Gewinnbereich''' (auch Gewinnzone genannt) ist jenes Intervall, bei dem der Gewinn $G(x)>0$ ist. | ||
* Das '''Gewinnmaximum $G_{max}$''' wird mithilfe des [[Extremstellen|Hochpunktes]] der Gewinnfunktion bestimmt. | * Das '''Gewinnmaximum $G_{max}$''' wird mithilfe des [[Extremstellen|Hochpunktes]] der Gewinnfunktion bestimmt. | ||
| Zeile 309: | Zeile 323: | ||
| − | {{Vorlage:Beispiel|1=Gegeben | + | {{Vorlage:Beispiel|1=Gegeben sind die Kosten- und die Preisfunktion eines Betriebes: |
$$K(x)=0.017x^3−0.38x^2+3.3x+10$$ | $$K(x)=0.017x^3−0.38x^2+3.3x+10$$ | ||
$$p(x)=−0.25x+5$$ | $$p(x)=−0.25x+5$$ | ||
| Zeile 321: | Zeile 335: | ||
d) Fertigen Sie eine Skizze der Gewinnfunktion an und markieren Sie den Gewinnbereich, den Break-even-Point und das Gewinnmaximum. | d) Fertigen Sie eine Skizze der Gewinnfunktion an und markieren Sie den Gewinnbereich, den Break-even-Point und das Gewinnmaximum. | ||
<br> | <br> | ||
| − | e) Ermitteln Sie graphisch die Steigung der Gewinnfunktion bei x=7 ME. Überprüfen Sie Ihr Ergebnis rechnerisch. | + | e) Ermitteln Sie graphisch die Steigung der Gewinnfunktion bei $x=7$ ME. Überprüfen Sie Ihr Ergebnis rechnerisch. |
|2= | |2= | ||
| Zeile 329: | Zeile 343: | ||
$$G(x)=-0.25x^2+5x-0.017x^3+0.38x^2-3.3x-10$$ | $$G(x)=-0.25x^2+5x-0.017x^3+0.38x^2-3.3x-10$$ | ||
$$\underline{G(x)=-0.017x^3+0.13x^2+1.7x-10}$$ | $$\underline{G(x)=-0.017x^3+0.13x^2+1.7x-10}$$ | ||
| + | <br> | ||
| − | b) Der Gewinnbereich ist jener Bereich, wo $G(x)\geq 0$ gilt. Somit bestimmen wir zuerst die Nullstellen mit $G(x)=0$ | + | b) Der Gewinnbereich ist jener Bereich, wo $G(x)\geq 0$ gilt. Somit bestimmen wir zuerst die Nullstellen mit $G(x)=0$. |
$$G(x)=-0.017x^3+0.13x^2+1.7x-10$$ | $$G(x)=-0.017x^3+0.13x^2+1.7x-10$$ | ||
$$0=-0.017x^3+0.13x^2+1.7x-10$$ | $$0=-0.017x^3+0.13x^2+1.7x-10$$ | ||
| Zeile 336: | Zeile 351: | ||
erhalten wir: | erhalten wir: | ||
$$\underline{x_1=5.22 \textrm{ und } x_2=11.90}$$ | $$\underline{x_1=5.22 \textrm{ und } x_2=11.90}$$ | ||
| − | Somit ist der Gewinnbereich das [[Intervall]] $[5.22;11.90]$ | + | Somit ist der Gewinnbereich das [[Intervall]] $[5.22;11.90]$. |
| − | + | <br> | |
| + | <br> | ||
c) Das Gewinnmaximum erhalten wir, indem wir den [[Extremstellen|Hochpunkt]] der Gewinnfunktion bestimmen. Somit müssen wir zuerst die erste Ableitung bestimmen und dann die Gleichung $G'(x)=0$ lösen: | c) Das Gewinnmaximum erhalten wir, indem wir den [[Extremstellen|Hochpunkt]] der Gewinnfunktion bestimmen. Somit müssen wir zuerst die erste Ableitung bestimmen und dann die Gleichung $G'(x)=0$ lösen: | ||
$$G(x)=-0.017x^3+0.13x^2+1.7x-10$$ | $$G(x)=-0.017x^3+0.13x^2+1.7x-10$$ | ||
$$G'(x)=-0.051 x² + 0.26x + 1.7$$ | $$G'(x)=-0.051 x² + 0.26x + 1.7$$ | ||
$$0=-0.051 x² + 0.26x + 1.7$$ | $$0=-0.051 x² + 0.26x + 1.7$$ | ||
| − | Lösen wir die [[Quadratische Gleichungen|quadratische Gleichung]] (z.B. mit der großen Lösungsformel oder mit Quadkom), so erhalten wir: | + | Lösen wir die [[Quadratische Gleichungen|quadratische Gleichung]] (z. B. mit der großen Lösungsformel oder mit Quadkom), so erhalten wir: |
$$x_1=-3.76 \textrm{ und } x_2=8.86$$ | $$x_1=-3.76 \textrm{ und } x_2=8.86$$ | ||
| − | Da eine negative Menge für den maximalen Gewinn nicht infrage kommt, bleibt nur noch $x_2=8.86$ als | + | Da eine negative Menge für den maximalen Gewinn nicht infrage kommt, bleibt nur noch $x_2=8.86$ als mögliche Stelle für das Gewinnmaximum übrig. |
| − | Ob sich hier wirklich ein Hochpunkt befindet, können wir z.B. mithilfe der 2. Ableitung herausfinden: | + | Ob sich hier wirklich ein Hochpunkt befindet, können wir z. B. mithilfe der 2. Ableitung herausfinden: |
$$G''(x)=-0.102 x + 0.26 $$ | $$G''(x)=-0.102 x + 0.26 $$ | ||
$$G''(8.86)=-0.102 8.86 + 0.26 <0 \rightarrow \textrm{ Hochpunkt}$$ | $$G''(8.86)=-0.102 8.86 + 0.26 <0 \rightarrow \textrm{ Hochpunkt}$$ | ||
Somit befindet sich der maximale Gewinn bei $x_{max}=8.86$ ME. Der maximale Gewinn beträgt: | Somit befindet sich der maximale Gewinn bei $x_{max}=8.86$ ME. Der maximale Gewinn beträgt: | ||
$$G(x_{max})=G(8.86)=-0.017\cdot 8.86^3+0.13\cdot 8.86^2+1.7\cdot 8.86-10=3.44\textrm{ GE}$$ | $$G(x_{max})=G(8.86)=-0.017\cdot 8.86^3+0.13\cdot 8.86^2+1.7\cdot 8.86-10=3.44\textrm{ GE}$$ | ||
| + | <br> | ||
| − | + | d) Mithilfe des Gewinnbereichs und des Gewinnmaximums bei $(8.86\vert 3.44)$ und ein paar weiterer berechneter Punkte (siehe Wertetabelle) erhalten wir den Graphen der Gewinnfunktion: | |
| − | + | ||
| − | d) Mithilfe des Gewinnbereichs und des Gewinnmaximums bei $(8.86\vert 3.44)$ und ein paar weiterer berechneter Punkte (siehe Wertetabelle | + | |
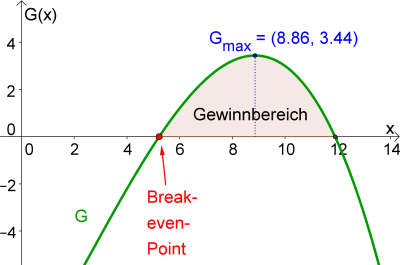
[[Datei:Gewinnbereich-Gmax.png|400px|mini|zentriert|Graph der Gewinnfunktion mit Gewinnbereich, dem Break-even-Point und dem Gewinnmaximum]] | [[Datei:Gewinnbereich-Gmax.png|400px|mini|zentriert|Graph der Gewinnfunktion mit Gewinnbereich, dem Break-even-Point und dem Gewinnmaximum]] | ||
| + | <br> | ||
[[Datei:Grenzgewinn.png|350px|mini|rechts|Tangente an die Gewinnfunktion bei x=7]] | [[Datei:Grenzgewinn.png|350px|mini|rechts|Tangente an die Gewinnfunktion bei x=7]] | ||
| − | e) Zeichnet man die Tangente an die Gewinnfunktion bei x=7 und anschließend das Steigungsdreieck ein, so erhält man eine Steigung von ca. 1. | + | e) Zeichnet man die Tangente an die Gewinnfunktion bei $x=7$ und anschließend das Steigungsdreieck ein, so erhält man eine Steigung von ca. $1$. |
Rechnerisch erhalten wir die Steigung mithilfe der 1. Ableitung an der Stelle $x=7$: | Rechnerisch erhalten wir die Steigung mithilfe der 1. Ableitung an der Stelle $x=7$: | ||
$$G'(x)=-0.051 x² + 0.26x + 1.7$$ | $$G'(x)=-0.051 x² + 0.26x + 1.7$$ | ||
$$G'(7)=1.02$$ | $$G'(7)=1.02$$ | ||
| − | Erhöht man die Produktionsmenge bei $x=7$ um eine weitere Einheit, so beträgt der zusätzliche Gewinn ca. 1.02 GE (=Grenzgewinn bei $x=7$) | + | Erhöht man die Produktionsmenge bei $x=7$ um eine weitere Einheit, so beträgt der zusätzliche Gewinn ca. $1.02$ GE (= Grenzgewinn bei $x=7$). |
| + | <br> | ||
| + | <br> | ||
}} | }} | ||
| Zeile 370: | Zeile 388: | ||
=== Der Cournot'sche Punkt === | === Der Cournot'sche Punkt === | ||
| − | [[Datei:Cournot-scherPunkt-allgemein.png|400px|mini|rechts|Graph der Preisfunktion mit dem | + | [[Datei:Cournot-scherPunkt-allgemein.png|400px|mini|rechts|Graph der Preisfunktion mit dem Cournot'schen Punkt $(x_{max}\vert p(x_{max}))$]] |
| − | {{Vorlage:Merke|1= '''Der | + | {{Vorlage:Merke|1= '''Der Cournot'sche Punkt''' |
| − | Sei $x_{max}$ jene Menge, bei der der Gewinn maximal ist und $p(x_{max})$ der Preis bei dieser Menge. Dann bezeichnet der Punkt $(x_{max} \vert p(x_{max}))$ den ''' | + | Sei $x_{max}$ jene Menge, bei der der Gewinn maximal ist und $p(x_{max})$ der Preis bei dieser Menge. Dann bezeichnet der Punkt $(x_{max} \vert p(x_{max}))$ den '''Cournot‘schen Punkt'''. Dieser liegt auf dem Graphen der Preisfunktion $p$.}} |
| − | Der | + | Der Cournot'sche Punkt gibt somit an, bei welcher Menge der maximale Gewinn liegt und wie groß der Preis sein muss. |
| − | {{Vorlage:Beispiel|1= Der Preis ist gegeben durch die Preisfunktion p mit | + | {{Vorlage:Beispiel|1= Der Preis ist gegeben durch die Preisfunktion $p$ mit |
$$p(x)=−0.25x+5$$ | $$p(x)=−0.25x+5$$ | ||
Durch Analyse der Gewinnfunktion weiß das Unternehmen, dass der maximale Gewinn bei einer Menge von $x_{max}=8.86$ erzielt wird. | Durch Analyse der Gewinnfunktion weiß das Unternehmen, dass der maximale Gewinn bei einer Menge von $x_{max}=8.86$ erzielt wird. | ||
| − | + | <br> | |
| − | a) Berechnen Sie den dazugehörigen Preis pro Mengeneinheit, bei dem der maximale Gewinn erreicht wird. | + | <br> |
| − | b) Bestimmen Sie die Koordinaten des | + | a) Berechnen Sie den dazugehörigen Preis pro Mengeneinheit, bei dem der maximale Gewinn erreicht wird. |
| + | <br> | ||
| + | b) Bestimmen Sie die Koordinaten des Cournot'schen Punktes. | ||
|2= | |2= | ||
| − | [[Datei:Cournot-scherPunkt-Bsp.png|350px|mini|rechts|In den Graphen der Preisfunktion | + | [[Datei:Cournot-scherPunkt-Bsp.png|350px|mini|rechts|In den Graphen der Preisfunktion $p$ wurde der Cournot'sche Punkt eingezeichnet.]] |
a) Indem wir für $x_{max}=8.86$ in die Preisfunktion einsetzen, erhalten wir den passenden Preis: | a) Indem wir für $x_{max}=8.86$ in die Preisfunktion einsetzen, erhalten wir den passenden Preis: | ||
$$p(8.86)=−0.25\cdot 8.86+5$$ | $$p(8.86)=−0.25\cdot 8.86+5$$ | ||
$$p(8.86)=2.785$$ | $$p(8.86)=2.785$$ | ||
| − | Der maximale Gewinn wird bei einem Preis von 2.785 GE/ME erreicht. | + | Der maximale Gewinn wird bei einem Preis von $2.785$ GE/ME erreicht. |
| − | b) Die Koordinaten des | + | b) Die Koordinaten des Cournot'schen Punktes lauten |
$$P(x_{max}\vert p(x_{max})=(8.86\vert 2.785))$$ | $$P(x_{max}\vert p(x_{max})=(8.86\vert 2.785))$$ | ||
Dieser kann im Graphen der Preisfunktion markiert werden (siehe Abbildung rechts). | Dieser kann im Graphen der Preisfunktion markiert werden (siehe Abbildung rechts). | ||
| Zeile 399: | Zeile 419: | ||
| − | [ | + | [https://www1.vobs.at/maturawiki/index.php?action=ajax&title=-&rs=SecureFileStore::getFile&f=/4/42/%C3%9Cberblicksblatt_zur_Kosten-_und_Preistheorie.pdf Zusammenfassung aller wichtigen Begriffe der Kosten- und Preistheorie] |
| Zeile 428: | Zeile 448: | ||
{{Vorlage:Bifie-Aufgabe|1= https://aufgabenpool.srdp.at/bhs/download.php?qid=468&file=Reisekosten.pdf Reisekosten }} | {{Vorlage:Bifie-Aufgabe|1= https://aufgabenpool.srdp.at/bhs/download.php?qid=468&file=Reisekosten.pdf Reisekosten }} | ||
: für Aufgabe a) benötigst du auch Wissen über die [[Regression]] | : für Aufgabe a) benötigst du auch Wissen über die [[Regression]] | ||
| − | : für c) benötigst du Wissen über die [[Kurvendiskussionen]] und das [[Ableitung bestimmen| | + | : für c) benötigst du Wissen über die [[Kurvendiskussionen]] und das [[Ableitung bestimmen| Bestimmen der Ableitungsfunktion]] |
{{Vorlage:Bifie-Aufgabe|1= https://aufgabenpool.srdp.at/bhs/download.php?qid=428&file=Erweiterung_der_Produktpalette.pdf Erweiterung der Produktionspalette }} | {{Vorlage:Bifie-Aufgabe|1= https://aufgabenpool.srdp.at/bhs/download.php?qid=428&file=Erweiterung_der_Produktpalette.pdf Erweiterung der Produktionspalette }} | ||
Aktuelle Version vom 25. März 2020, 16:30 Uhr
Die folgenden zwei Videos zeigen geben dir eine Zusammenfassung aller wichtigen Punkte der Kosten- und Preistheorie. Details zu den einzelnen Begriffen findest du unterhalb der Videos.
| Auflistung aller wichtigen Begriffe | Beispiel |
|---|---|
Inhaltsverzeichnis
Preisfunktion der Nachfrage
|
Die Preisfunktion der Nachfrage, auch „Nachfragefunktion“ oder „Preis-Absatz-Funktion“ genannt, gibt den Preis $p$ in Abhängigkeit der produzierten Menge $x$ an. |
|
$ $
$$p_h=p(0)$$
$$p(x_S)=0$$
|
Eine Firma kann von ihrem Produkt $5$ Mengeneinheiten verkaufen, wenn sie den Preis auf $3.75€$ pro Stück festlegt. Senkt sie den Preis auf $2.50€$ pro Stück, so kann sie $10$ Mengeneinheiten des Produktes verkaufen.
- Modellieren Sie die lineare Preisfunktion.
- Ermitteln Sie daraus den Höchstpreis und die Sättigungsmenge.
- Zuerst stellen wir die lineare Preisfunktion der Form $p(x)=k\cdot x+d$ auf, wobei $x$ die Mengeneinheiten und $p(x)$ den Preis pro Stück angibt.
1. Variante: Wir setzen die Punkte $(5\vert 3.75)$ und $(10\vert 2.50)$ in die Funktionsgleichung ein und berechnen $k$ und $d$, indem wir das Gleichungssystem lösen (hierbei eignet sich z. B. das Additionsverfahren): $$p(x)=k\cdot x+d$$
- 1. Punkt: $I:\ \ 3.75= k\cdot 5+d$
- 2. Punkt: $\underline{II:2.50=k\cdot 10+d\ \ "-"}$
$$\ \ \ \ 1.25=-5\cdot k\ \ \ \rightarrow k=-0.25 \rightarrow d=5$$ Somit erhalten wir die Preisfunktion $p$ mit $$p(x)=-0.25x+5$$

2. Variante: Da es sich um eine lineare Funktion handelt, kann $k$ auch mithilfe des Steigungsdreiecks bei den Punkten $(5\vert 3.75)$ und $(10\vert 2.50)$ ermittelt werden: $$k=\frac{\Delta y}{\Delta x}=\frac{Höhenunterschied}{Längenunterschied}=\frac{2.50-3.75}{10-5}=-0.25$$ Somit ist $k=-0.25$. Um $d$ zu berechnen, setzt man einen der beiden Punkte und $k$ in die Funktionsgleichung ein: Punkt $(5\vert 3.75)$ und $k=-0.25$ in $p(x)=k\cdot x+d$ eingesetzt ergeben: $$3.75=-0.25\cdot 5+d$$ $$\rightarrow 3.75+1.25=d \rightarrow d=5$$ Somit erhalten wir: $$p(x)=-0.25\cdot x+5$$
- Nun bestimmen wir mit der Preisfunktion den Höchstpreis und die Sättigungsmenge:
- Höchstpreis: $p(0)=d=5$.
- Der Höchstpreis beträgt $5€$ pro Mengeneinheit.
- Sättigungsmenge: $p(x)=0$
$$0=-0.25x+5$$ $$-5=-0.25x$$ $$x=20$$
- Die Sättigungsmenge beträgt somit $20$ Mengeneinheiten.
Erlösfunktion
Allgemein
|
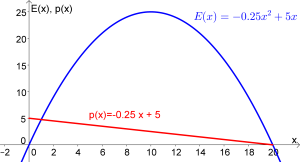
Der Gesamterlös $E$ (auch Umsatz genannt) ergibt sich aus dem Produkt der verkauften Menge und dem dazugehörigen Preis:
$$E(x)=x\cdot p(x)$$ |
Gegeben ist die Preisfunktion $p$ mit $p(x)=-0.25x+5$.
- Stellen Sie die dazugehörige Erlösfunktion auf.
- Bestimmen Sie die sogenannten Erlösgrenzen, dies sind die Nullstellen der Erlösfunktion.
- Berechnen Sie den maximalen Erlös.
- Die Erlösfunktion erhalten wir mit:
$$E(x)=x\cdot p(x)$$ $$E(x)=x\cdot (-0.25x+5$$ $$E(x)=-0.25x^2+5x$$
- Die Nullstellen ermitteln wir, indem wir die Erlösfunktion gleich null setzen:
$$0=E(x)$$ $$0=-0.25x^2+5x$$ Durch herausheben von $x$, Quadkom oder den Löse-Befehl erhalten wir $x_1=0$ und $x_2=20$.
- Nun bestimmen wir den maximalen Erlös:
1. Variante: Mithilfe der Eigenschaften einer quadratischen Funktion.
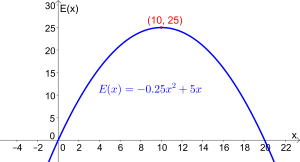
Die Erlösfunktion $E$ mit $E(x)=-0.25x^2+5x$ ist eine quadratische Funktion mit $2$ Nullstellen. Wie jede quadratische Funktion hat sie aufgrund ihrer Symmetrie ihren Scheitelpunkt (Extremstelle) genau zwischen den beiden Nullstellen. $$x_{max}=\frac{0+20}{2}=10$$ Das Erlösmaximum befindet sich somit bei $x=10$ Mengeneinheiten. Der Erlös beträgt $E(10)=25$ Geldeinheiten.
2. Variante: Mithilfe des Maximum-Befehls (siehe Ti-Taschenrechner bzw. GeoGebra). Das Ergebnis siehst du in der rechten Abbildung
3. Variante: Mithilfe der Differentialrechnung. Für ein Maximum muss gelten, dass $f'(x)=0$ und $f''(x)<0$ ist: $$E'(x)=-0.5x+5$$ $$0=-0.5x+5\ \ \ \rightarrow x=10$$ Und nun zur 2. Ableitung: $$E''(x)=-0.5$$ $$ E''(10)=-0.5<0 \ \ \ \rightarrow HP$$ Somit befindet sich bei $x=10$ ein Hochpunkt und der Erlös an dieser Stelle beträgt $E(10)=25$.
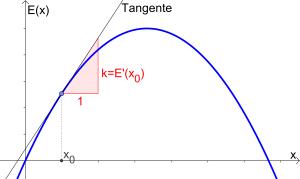
Grenzerlös
|
Der Grenzerlös $E'(x)$ gibt die (ungefähre) Zunahme/Abnahme des Erlöses an, wenn eine weitere Mengeneinheit produziert wird. |
- Bestimmen Sie den Grenzerlös der Erlösfunktion $E$ mit $E(x)=-0.25x^2+5x$ bei einer Menge von $x=5$ ME und interpretieren Sie das Ergebnis.
Hinweis!
Kostenfunktion
Definition und Aufbau der Kostenfunktion
|
Die Gesamtkosten für die Produktion werden durch die Kostenfunktion $K$ angegeben. Die Kostenfunktion besteht dabei aus $2$ Termen:
$$K(x)=K_v (x)+F$$ $K_v (x)...$ variable Kosten (jene Kosten, die von der produzierten Menge $x$ abhängig sind) $F...$ Fixkosten, die auch bei einer Produktion von $0$ ME anfallen. |
|
Typische Eigenschaften einer "ertragsgesetzlichen Kostenfunktion"
|
Gegeben ist die Kostenfunktion $K$ mit
$$K(x)=0.017x^3−0.38x^2+3.3x+10$$
a) Bestimmen Sie die Fixkosten und die variablen Kosten der Funktion.
b) Berechnen Sie die Kosten bei einer Produktion von $12$ ME. Geben Sie auch an, wie hoch die variablen Kosten sind.
c) Ermitteln Sie die Produktionsmenge, wenn Kosten von $60$ GE anfallen.
a) Die Kostenfunktion lautet $K(x)=0.017x^3−0.38x^2+3.3x+10$. Der konstante Term gibt die Fixkosten an, der Term mit den $x$ gibt die variablen Kosten an:
- Fixkosten: $10$
- Variable Kosten: $0.017x^3−0.38x^2+3.3x$
b) Gefragt sind die Kosten bei $x=12$ ME und gesucht ist $K(12)$:
$$K(12)=0.017\cdot 12 ^3−0.38 \cdot 12^2+3.3\cdot 12+10=24.256 \textrm{ GE}$$
c) Die Kosten betragen $K(x)=60$ und gesucht ist $x$: $$60=0.017x^3−0.38x^2+3.3x+10$$ Mithilfe von Technologie (siehe TI-Befehle bzw. GeoGebra) erhalten wir: $$x=20$$ A: Bei einer Produktion von $20$ ME fallen Kosten von $60$ GE an.
Grenzkosten
|
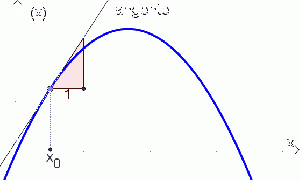
Die Grenzkosten $K'(x)$ geben die (ungefähre) Zunahme/Abnahme der Kosten an, wenn eine weitere Mengeneinheit produziert wird. $K'(x)$ bezeichnet dabei die 1. Ableitung von $K(x)$. |
Bild mit Tangente und Steigungsdreieck
Gegeben ist die Kostenfunktion $$K(x)=0.017x^3−0.38x^2+3.3x+10$$
- Bestimmen Sie die Grenzkosten bei einer Produktionsmenge von $20$ ME.
- Interpretieren Sie das Ergebnis.
$$K(x)=0.017x^3−0.38x^2+3.3x+10$$ $$K'(x)=0.051x^2-0.76x+3.3$$ $K'(x)$ gibt uns die Grenzkostenfunktion an. Nun müssen wir nur noch die Grenzkosten bei $20$ ME, d. h. $K'(20)$ bestimmen: $$K'(20)=0.051\cdot 20^2-0.76\cdot 20+3.3$$ $$K'(20)=8.5\textrm{ GE/ME} $$ Die Grenzkosten bei einer Produktionsmenge von $x=20$ ME betragen $8.5$ GE/ME.
Interpretation: Bei einer Produktion von $20$ Mengeneinheiten fallen für eine zusätzlich produzierte $21$. Mengeneinheit Kosten von ca. $8.5$ GE/ME an.
Stückkostenfunktion, Betriebsoptimum und langfristige Preisuntergrenze
|
Die Stückkosten $\bar{K}(x)$ geben die durchschnittlichen Kosten pro Stück (oder Mengeneinheit) an und berechnen sich, indem die Gesamtkosten durch die Stückzahlen dividiert werden, d. h. mit
$$\bar{K}(x)=\frac{K(x)}{x}$$ $x...$ Anzahl der produzierten Stückzahlen (oder Mengeneinheiten). $K(x)...$ Gesamtkosten $\bar{K}(x)...$ durchschnittliche Kosten pro Stück/Mengeneinheit |
Interessant bei den durchschnittlichen Kosten ist jene Stelle, bei der die Kosten pro Stück minimal sind. Diese Stelle nennt man das
|
Betriebsoptimum $x_{opt}$
... ist jene Stelle, bei der die Stückkosten $\bar{K}(x)$ ein Minimum (Tiefpunkt) haben. Die dazugehörigen Stückkosten $\bar{K}(x_{opt})$ nennt man langfristige Preisuntergrenze (oder auch kostendeckender Preis). |
Gegeben ist die Kostenfunktion $K$ mit $$K(x)=0.017x^3 - 0.38x^2 + 3.3x + 10$$
- Berechnen Sie das Betriebsoptimum und die langfristige Preisuntergrenze.
$$K(x)=0.017x^3 - 0.38x^2 + 3.3x + 10$$ $$\bar{K}(x)=\frac{0.017x^3 - 0.38x2 + 3.3x + 10}{x}$$ $$\bar{K}(x)=0.017x^2 - 0.38x + 3.3 +\frac{10}{x}$$ $$\bar{K}(x)=0.017x^2 - 0.38x + 3.3+10x^{-1}$$
Nun berechnen wir das Minimum der Stückkostenfunktion. Entweder mit dem Minimumbefehl (TI-Befehle,GeoGebra) oder (wie hier) mithilfe der Differentialrechnung (siehe Ableitung bestimmen bzw. Kurvendiskussionen):
Um das Minimum zu berechnen, ermitteln wir zuerst $\bar{K}'(x)$ und setzen dies dann gleich $0$: $$\bar{K}'(x)=0.034x - 0.38 -10x^{-2}$$ $$0=0.034x - 0.38 -10x^{-2}\ \ \ \ \vert \cdot x^2$$ $$0=0.034x^3-0.38x^2-10$$ Diese Gleichung löst man am besten graphisch (siehe TI-Befehle bzw. GeoGebra) oder mit dem Löse-Befehl (siehe TI-Befehle bzw. GeoGebra) und erhält: $$x_{opt}=12.93$$
Antwort: Das Betriebsoptimum liegt bei $12.93$ Mengeneinheiten.
Die dazugehörenden Stückkosten, die sogenannte langfristige Preisuntergrenze, liegen bei: $$\bar{K}(x_{opt})=\bar{K}(12.93)= 2 \textrm{ GE pro ME}$$
Variable Stückkostenfunktion, Betriebsminimum und kurzfristige Preisuntergrenze
|
Die variablen Stückkosten $\bar{K_v}(x)$ geben die durchschnittlichen variablen Kosten pro Stück an.
$$\bar{K_v}(x)=\frac{K_v(x)}{x}$$ (Hinweis: $\bar{K_v}$ ist jener Term von $K(x)$ ohne die Fixkosten $F$). |
Auch hier interessieren wir uns für jene Stelle, an der die variablen Stückkosten minimal sind:
|
Das Betriebsminimum $x_{min}$ ist jene Stelle, bei der die variablen Stückkosten minimal sind.
Die dazugehörenden variablen Stückkosten $\bar{K_v}(x_{min})$ werden kurzfristige Preisuntergrenze genannt. |
Gegeben ist die Kostenfunktion $K$ mit $$K(x)=0.017x^3−0.38x^2+3.3x+10$$ Bestimmen Sie
- die variablen Kosten $K_v (x)$,
- die variable Stückkostenfunktion $\bar{K_v}(x)$ sowie
- das Betriebsminimum zusammen mit der kurzfristigen Preisuntergrenze.
$$K_v (x)=0.017x^3−0.38x^2+3.3x$$
- daraus erhalten wir die variable Stückkostenfunktion
$$\bar{K_v}(x)=\frac{0.017x^3−0.38x^2+3.3x}{x}=0.017x^2−0.38x+3.3$$
- Nun müssen wir für das Betriebsminimum nur noch das Minimum der Stückkostenfunktion bestimmen:
$$\bar{K_v}(x)=0.017x^2−0.38x+3.3$$ $$\bar{K_v}'(x)=0.034x-0.38$$ $$0=0.034x-0.38\ \rightarrow \underline{\underline{x_{min}= 11.18} }$$ Das Betriebsminimum liegt somit bei $11.18$ Mengeneinheiten.
Zuletzt berechnen wir noch die kurzfristige Preisuntergrenze $\bar{K_v}(x_{min})$: $$\bar{K_v}(x)=0.017x^2−0.38x+3.3$$ $$\bar{K_v}(11.18)=0.017\cdot 11.18^2−0.38\cdot 11.18+3.3$$ $$\underline{\underline{\bar{K_v}(x)=1.18} }$$ Die kurzfristige Preisuntergrenze beträgt somit $1.18$ GE und wird erreicht, wenn $x_{min}=11.18$ ME produziert werden.
Gewinnfunktion
Allgemein
Mithilfe des Erlöses (Umsatz) und der Kosten können wir nun den Gewinn berechnen:
|
Sei $x$ die Menge der produzierten und zugleich verkauften Mengeneinheiten, dann erhält man den Gewinn $G$ aus
$$G(x)=E(x)-K(x)$$ Der Gewinn ergibt sich, wenn man vom Erlös die Kosten abzieht. |
Folgende Punkte sind bei der Analyse der Gewinnfunktion relevant:
|
$ $
|
Gegeben sind die Kosten- und die Preisfunktion eines Betriebes:
$$K(x)=0.017x^3−0.38x^2+3.3x+10$$
$$p(x)=−0.25x+5$$
a) Ermitteln Sie die Gewinnfunktion.
b) Bestimmen Sie den Gewinnbereich.
c) Berechnen Sie das Gewinnmaximum.
d) Fertigen Sie eine Skizze der Gewinnfunktion an und markieren Sie den Gewinnbereich, den Break-even-Point und das Gewinnmaximum.
e) Ermitteln Sie graphisch die Steigung der Gewinnfunktion bei $x=7$ ME. Überprüfen Sie Ihr Ergebnis rechnerisch.
$$ G(x)=E(x)-K(x)$$
$$G(x)=x\cdot (-0.25x+5)-(0.017x^3−0.38x^2+3.3x+10)$$
$$G(x)=-0.25x^2+5x-0.017x^3+0.38x^2-3.3x-10$$
$$\underline{G(x)=-0.017x^3+0.13x^2+1.7x-10}$$
b) Der Gewinnbereich ist jener Bereich, wo $G(x)\geq 0$ gilt. Somit bestimmen wir zuerst die Nullstellen mit $G(x)=0$.
$$G(x)=-0.017x^3+0.13x^2+1.7x-10$$
$$0=-0.017x^3+0.13x^2+1.7x-10$$
Mithilfe von Technologie (für den TI-Taschenrechner eignet sich hier der zero-Befehl)
erhalten wir:
$$\underline{x_1=5.22 \textrm{ und } x_2=11.90}$$
Somit ist der Gewinnbereich das Intervall $[5.22;11.90]$.
c) Das Gewinnmaximum erhalten wir, indem wir den Hochpunkt der Gewinnfunktion bestimmen. Somit müssen wir zuerst die erste Ableitung bestimmen und dann die Gleichung $G'(x)=0$ lösen:
$$G(x)=-0.017x^3+0.13x^2+1.7x-10$$
$$G'(x)=-0.051 x² + 0.26x + 1.7$$
$$0=-0.051 x² + 0.26x + 1.7$$
Lösen wir die quadratische Gleichung (z. B. mit der großen Lösungsformel oder mit Quadkom), so erhalten wir:
$$x_1=-3.76 \textrm{ und } x_2=8.86$$
Da eine negative Menge für den maximalen Gewinn nicht infrage kommt, bleibt nur noch $x_2=8.86$ als mögliche Stelle für das Gewinnmaximum übrig.
Ob sich hier wirklich ein Hochpunkt befindet, können wir z. B. mithilfe der 2. Ableitung herausfinden:
$$G''(x)=-0.102 x + 0.26 $$
$$G''(8.86)=-0.102 8.86 + 0.26 <0 \rightarrow \textrm{ Hochpunkt}$$
Somit befindet sich der maximale Gewinn bei $x_{max}=8.86$ ME. Der maximale Gewinn beträgt:
$$G(x_{max})=G(8.86)=-0.017\cdot 8.86^3+0.13\cdot 8.86^2+1.7\cdot 8.86-10=3.44\textrm{ GE}$$
d) Mithilfe des Gewinnbereichs und des Gewinnmaximums bei $(8.86\vert 3.44)$ und ein paar weiterer berechneter Punkte (siehe Wertetabelle) erhalten wir den Graphen der Gewinnfunktion:
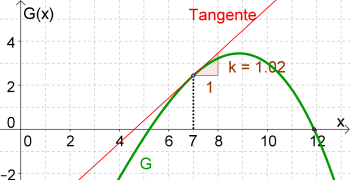
e) Zeichnet man die Tangente an die Gewinnfunktion bei $x=7$ und anschließend das Steigungsdreieck ein, so erhält man eine Steigung von ca. $1$.
Rechnerisch erhalten wir die Steigung mithilfe der 1. Ableitung an der Stelle $x=7$: $$G'(x)=-0.051 x² + 0.26x + 1.7$$ $$G'(7)=1.02$$ Erhöht man die Produktionsmenge bei $x=7$ um eine weitere Einheit, so beträgt der zusätzliche Gewinn ca. $1.02$ GE (= Grenzgewinn bei $x=7$).
Der Cournot'sche Punkt
|
Der Cournot'sche Punkt
Sei $x_{max}$ jene Menge, bei der der Gewinn maximal ist und $p(x_{max})$ der Preis bei dieser Menge. Dann bezeichnet der Punkt $(x_{max} \vert p(x_{max}))$ den Cournot‘schen Punkt. Dieser liegt auf dem Graphen der Preisfunktion $p$. |
Der Cournot'sche Punkt gibt somit an, bei welcher Menge der maximale Gewinn liegt und wie groß der Preis sein muss.
Der Preis ist gegeben durch die Preisfunktion $p$ mit
$$p(x)=−0.25x+5$$
Durch Analyse der Gewinnfunktion weiß das Unternehmen, dass der maximale Gewinn bei einer Menge von $x_{max}=8.86$ erzielt wird.
a) Berechnen Sie den dazugehörigen Preis pro Mengeneinheit, bei dem der maximale Gewinn erreicht wird.
b) Bestimmen Sie die Koordinaten des Cournot'schen Punktes.
a) Indem wir für $x_{max}=8.86$ in die Preisfunktion einsetzen, erhalten wir den passenden Preis: $$p(8.86)=−0.25\cdot 8.86+5$$ $$p(8.86)=2.785$$ Der maximale Gewinn wird bei einem Preis von $2.785$ GE/ME erreicht.
b) Die Koordinaten des Cournot'schen Punktes lauten $$P(x_{max}\vert p(x_{max})=(8.86\vert 2.785))$$ Dieser kann im Graphen der Preisfunktion markiert werden (siehe Abbildung rechts).
Übungs- und Überblicksdokumente
? Arbeitsblatt zum lösen von Aufgaben (Kurt Söser) Wichtig!
Zusammenfassung aller wichtigen Begriffe der Kosten- und Preistheorie
Maturaaufgaben
| Vorgerechnetes Video-Beispiel |
|---|
- für Aufgabe a) benötigst du auch Wissen über die Umkehraufgaben
- für Aufgabe a) benötigst du auch Wissen über die Regression
- für Aufgabe a) benötigst du auch Wissen über die Regression
- für Aufgabe a) benötigst du auch Wissen über die Regression
- für c) benötigst du Wissen über die Kurvendiskussionen und das Bestimmen der Ableitungsfunktion
$Bifie$ Erweiterung der Produktionspalette
- für b) benötigst du Wissen über die Rentenrechnung
- für Aufgabe c) benötigst du auch Wissen über die Wahrscheinlichkeitsrechnung (5. Klasse)