Zins- und Zinseszinsrechnung
Inhaltsverzeichnis
Warum gibt es Zinsen?
- Leihgebür
- Wenn jemand einem anderen Geld verleiht, verlangt er dafür eine Leihgebür in Form von Zinsen
- Risiko-Gebühr
- Jeder, der Geld verleiht, geht das Risiko ein, dass er das Geld nicht wieder zurückbekommt. Die Zinsen können hierbei als Absicherung gesehen werden. Je höher das Risiko eines Verlusts, desto größer sind auch die Zinsen.
Begriffe
- $K_0 \dots $ Anfangskapital (=Kapital am Anfang/ im Jahre 0)
- $n \dots $ Anzahl der Verzinsungen
- $K_n \dots $ Kapital nach n Jahren
- $i \dots $ Zinssatz (z.B. 4 % p.a.)
- $i_{eff}\dots $ effektiver Zinssatz = Zinssatz mit abgezogener Kapitalertragssteuer (KESt). Im Allgemeinen gilt bei 25 % KESt: $$ i_{eff}=i\cdot 0.75$$ (z.B. i=4 % $ \rightarrow i_{eff}=4\cdot 0.75=3$ %)
- $r\dots $ Aufzinsungsfaktor ($r=1+\frac{i}{100})$
Einfache Zinsen
Formel für die einfachen Zinsen
| Formel für die einfache Verzinsung |
|---|
| Sei n die Veranlagungsdauer in Jahren, dann gilt:
$$ K_n=K_0 + n\cdot \frac{i_{eff}}{100} \cdot K_0 $$und vereinfacht:$$ K_n=K_0 \cdot ( 1+n\cdot \frac{i_{eff}}{100} ) $$ |
Hinweis!
Anna hat $K_0$ Euro auf der Bank bei einer jährichen Verzinsung von i % p.a. (per anno = pro Jahr). Somit erhält sie nach einem Jahr zusätzlich "i % von $K_0$".Das Kapital nach einem Jahr beträgt dann $$K_1=K_0+\textrm{ i % von } K_0$$ $$K_1=K_0+\frac{i}{100}\cdot K_0$$ $$K_1=K_0\cdot (1+\frac{i}{100} )$$
Nun will Anna das Geld aber schon nach 7 Monaten abheben. Da die Bank ihr 5 % für das ganze Jahr versprochen hat, Anna das Geld aber bereits nach $\frac{7}{12}$ des Jahres abhebt, erhält sie nur $\frac{7}{12}$ der Zinsen. Damit ergibt sich: $$K_{ \frac{7}{12} }=K_0+\frac{7}{12}\textrm{ der i }\% \textrm{ von } K_0$$ $$K_{\frac{7}{12} }=K_0 + \frac{7}{12} \frac{i}{100}\cdot K_0$$ $$K_{\frac{7}{12} }=K_0\cdot (1+ \frac{i}{100} \cdot \frac{7}{12})$$
Verallgemeinerung:
Angenommen das Kapital liegt nicht $\frac{7}{12})$ des Jahres auf dem Konto, sondern $n$, wobei $n$ die Zeit in Jahren angibt, so gilt: $$K_{\frac{7}{12} }=K_0\cdot (1+ \frac{i}{100} \cdot n)$$
|
Die einfachen Zinsen werden verwendet, wenn ...
Bei den einfachen Zinsen handelt es sich um ein lineares Wachstum |
Variante 1: Kapital wird vor dem Ende der Zinsperiode abgehoben
€ 30 Euro werden mit einem effektiven Zinssatz von 5 % p.a. (=per anno = pro Jahr) verzinst. Wie hoch ist das Kapital nach 9 Monaten.
- $K_0 =30 $
- $n = \frac{9}{12} $
- $K_{\frac{9}{12} } = $?
- $i_{eff} = 5$ %
$$ K_{\frac{9}{12} }=30\cdot (1+\frac{5}{100}\cdot \frac{9}{12} ) $$
$$ \underline{\underline{K_1 = 31.13} } $$
Antwort: Nach 9 Monaten beträgt das Endkapital € 31.13.
Variante 2: Zinsen werden erst am Ende der Laufzeit ausbezahlt
€ 30 sollen 4 Jahre lang mit effektiv 5 % p.a. einfach verzinst werden. Wie hoch ist das Endkapital? (einfach bedeutet hier: die Zinsen werden erst am Ende der 4 Jahre auf das Konto überwiesen)
- $K_0=30$
- $K_n=$ ?
- $i_{eff}=5$ %
- $n=4$
$$ K_n=K_0\cdot (1+\frac{i_{eff} }{100}\cdot n$$
$$ K_4 = 30 \cdot (1+\frac{5}{100} \cdot 4)$$
$$ K_4=36$$
$$ \underline{\underline{K_n=36} }$$
Antwort: Nach 4 Jahren beträgt das Kapital € 36.
Musterbeispiel für die einfache Verzinsung
Aufgabe: Ein Kapital von € 75 wird 4 Monate bei einem Zinssatz von 4 % p.a. veranlagt. Bestimme die Höhe des Kapitals nach der Veranlagungsdauer!
Lösung
- $K_0=75$
- $n=4 \textrm{ Monate }= \frac{4}{12}$ Jahre.
- $K_\frac{4}{12}=$?
- $i=4$ %
$$ K_n=K_0 \cdot ( 1+n\cdot \frac{i}{100} ) $$
$$ K_\frac{4}{12}=75\cdot (1+\frac{4}{12}\cdot \frac{4}{100}$$
$$ K_\frac{4}{12}=75\cdot (1+\frac{1}{3}\cdot \frac{1}{25}$$
$$ K_\frac{4}{12}=75\cdot (1+\frac{1}{75}) $$
$$ K_\frac{4}{12}=75\cdot (\frac{76}{75}) $$
$$ K_\frac{4}{12}=76 $$
Antwort: Nach 4 Monaten hat das Kapital eine Höhe von € 76.
Zinseszinsen
Zinseszinsformel
Bei einem Sparbuch erhält man für gewöhnlich jährlich Zinsen. Diese Zinsen werden im Anschluss wieder auf das Sparbuch gelegt. Im nächsten Jahr erhält man nun nicht nur Zinsen auf das ursprüngliche Kapital, sondern auch auf die Zinsen des letzten Jahrens - dies nennt man die Zinseszinsen.
Video: Herleitung der Zineszinsformel:
- $K_1=K_0+K_0\cdot \frac{i_{eff}}{100}=K_0\cdot (1+ \frac{i_{eff}}{100})$
- $K_2=\underbrace{K_1\cdot}_{K_0\cdot (1+ \frac{i_{eff}}{100})} (1+ \frac{i_{eff}}{100})=(K_0\cdot (1+ \frac{i_{eff}}{100}))\cdot (1+ \frac{i_{eff}}{100})=K_0\cdot (1+ \frac{i_{eff}}{100})^2$
- $K_n=K_0\cdot (1+ \frac{i_{eff}}{100})^n$
| Formel für die einfache Verzinsung |
|---|
| Sei n die Veranlagungsdauer, dann gilt: |
| $$ K_n=K_0\cdot (1+ \frac{i_{eff}}{100})^n$$ |
|
Die Zinseszinsformel wird verwendet, wenn über mehrere volle Jahre verzinst wird |
Musterbeispiele
- $K_n$ gefragt
- $K_0=800$
- $n=2$
- $i=2.5\ \% \rightarrow i_{eff}=2.5\cdot 0.75=1.875\ \%$
- $K_2=$?
$$ K_n=K_0\cdot (1+ \frac{i_{eff}}{100})^n$$
$$ K_n=800\cdot (1+ \frac{1.875}{100})^2$$$$ \underline{\underline{K_n=830.28}}$$
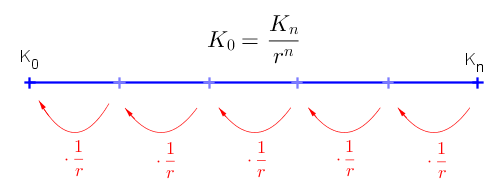
- $K_0$ gefragt
Welcher Betrag muss angespart werden, damit man nach 3 Jahren bei einem Zinssatz von 2,5 % p.a. über ein Guthaben von € 1500 verfügt, wenn die KESt zu berücksichtigen ist?
- $K_0=$?
- $n=3$
- $i=2.5 \% \rightarrow i_{eff}=2.5\cdot 0.75=1.875 \%$
- $K_3=1500$
$$ K_n=K_0\cdot (1+ \frac{i_{eff}}{100})^n$$$$ 1500=K_0\cdot (1+ \frac{1.875}{100})^3 $$
$$ \frac{1500}{(1+ \frac{1.875}{100})^3}=K_0$$
$$ \underline{\underline{K_0=1418.69}} $$
- $n$ gefragt
Wie viele volle Jahre muss ein Kapital von € 100 angespart werden, um bei einem Zinssatz von 2,5 % p.a. bei Berücksichtigung der KESt über ein Guthaben von mehr als € 200 zu verfügen? Siehe hier auch Verdoppelungszeit
- $K_0=100$
- $n=?$
- $i=2.5 \% \rightarrow i_{eff}=2.5\cdot 0.75=1.875 \%$
- $K_n=200$
$$ K_n=K_0\cdot (1+ \frac{i_{eff}}{100})^n$$$$ 200=100\cdot (1+ \frac{1.875}{100})^n \ \ |:100$$
$$ 2= (1+ \frac{1.875}{100})^n \ \ |\log() $$
$$ \log{2}=n\cdot \log{(1+ \frac{1.875}{100})} \ \ |:\log{(1+ \frac{1.875}{100})} $$
$$\frac{\log{2}}{\log{(1+ \frac{1.875}{100})}}=n $$
$$ \underline{\underline{n = 37.31}} $$
Antwort: Nach 38 vollen Jahren sind aus den € 100 mehr als € 200 geworden.
- $i$ gefragt
Mit welchem Zinssatz muss ein Sparbuch verzinst werden, damit ein Kapital von anfangs € 100 in 7 Jahren auf € 118.87 anwächst.
- $K_0=100$?
- $n=7$
- $i=? \%$
- $K_7=118.87$
$$ K_n=K_0\cdot (1+ \frac{i_{eff}}{100})^n$$$$ 118.87=100\cdot (1+ \frac{i_{eff}}{100})^7 \ \ |:100 \textrm{ und } |\sqrt[7]{ } $$
$$ \sqrt[7]{\frac{118.87}{100}}=1+ \frac{i_{eff}}{100}\ \ |-1 \textrm{ und } | \cdot 100 $$
$$ (\sqrt[7]{\frac{118.87}{100}}-1)\cdot 100 = i_{eff} $$
$$ \underline{\underline{i_{eff}=2.5}} $$
Antwort: Der effektive Zinssatz muss bei $i_{eff}=2.5$ % p.a. Somit muss der Zinssatz der Bank bei $i=\frac{i_{eff}}{0.75}=\frac{2.5}{0.75}=3.33$ % p.a. liegen.
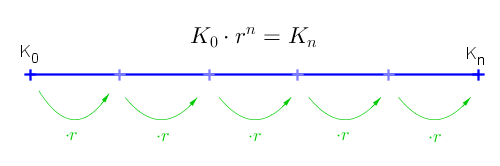
Aufzinsungsfaktor
Der Term$$ r=(1+\frac{i_{eff} }{100}) $$wird als Aufzinsungsfaktor bezeichnet. Damit vereinfacht sich die Zinseszinsformel zu:
| Zinseszinsformel |
|---|
| Sei n die Veranlagungsdauer, dann gilt:
$$ K_n=K_0\cdot r^n$$ |
|
$ $
|
Hinweis: Im offiziellen Formelheft für die Matura wird anstelle des Buchstabens r, der Buchstabe q verwendet. Somit lautet die Formel für die Zinseszinsrechnung auch
$$K_n=K_0\cdot q^n$$
Unterjährige Verzinsung
Nun betrachten wir auch Verzinsungen, die mehrmals im Jahr ("unterjährig") durchgeführt werden.
Begriffe: Sei $m$ die Anzahl der Verzinsungen in einem Jahr, dann ist
- m=2: halbjährige Verzinsung und $i_2$ % p.s. (pro Semester) der halbjährige Zinssatz
- m=4: vierteljährliche Verzinsung und $i_4$ % p.q. (pro Quartal) der Quartalszinssatz
- m=12: monatliche Verzinsung und $i_{12}$ % p.m. (pro Monat) der Monatszinssatz
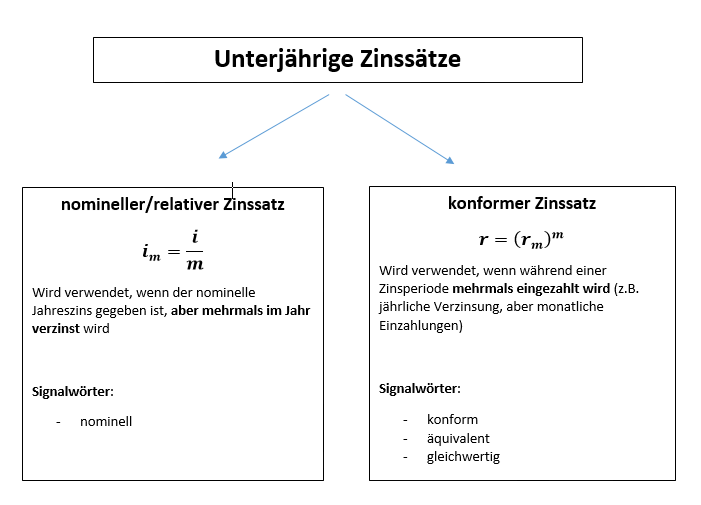
Es gibt nun zwei Arten, den unterjährigen Zinssatz zu bestimmen:
a) nomineller Jahreszins und relativer unterjähriger Zinssatz $i_m=\frac{i}{m}$
Der relative unterjährige Zinssatz wird verwendet, wenn der nominelle Jahreszins gegeben ist, aber mehrmals im Jahr verzinst wird
|
Sei i der nominelle Jahreszinssatz. Dann berechnet sich der nominelle unterjährige Zinssatz $i_m$:
$$ i_m=\frac{i}{m} $$ |
Der Nominalzinssatz beträgt $i=8$ % p.a.. Berechne den Quartalszinssatz $i_4$
|
Beim Verzinsen mit dem relativen unterjährigen Zinssatz erhält man über das ganze Jahr aufgrund des Zinseszinseffektes schlussendlich mehr als bei der einmaligen Verzinsung mit dem nominellen Jahreszinssatz! |
Das Problem mit dem nominellen Zinssatz ODER Warum gibt es den konformen Zinssatz
Problem: Nehmen wir an, wir verzinsen € 100 mit einem nominellen Jahreszinssatz von $i=4$ %. Nun fragt uns der Bankberater, ob wir einmal im Jahr verzinsen wollen mit $i=4$ %p.a., oder zweimal (d.h. halbjährlich) mit dem Halbjahreszinssatz von $i_2=\frac{4}{2}=2$ %p.s. Für was sollen wir uns entscheiden?
Antwort:
- Bei der jährlichen Verzinsung beträgt $K_1=104$ Euro.
- Aber bei der halbjährlichen Verzinsung erhalten wir:
$$K_1=K_0\cdot (1+\frac{2}{100})^2$$$$K_1=104.04$$
D.h. Mit der halbjährlichen Verzinsung würden wir 4 Cent mehr erhalten. Würde man sogar monatlich verzinsen, so erhielte man nach einem Jahr $K_1=100\cdot (1+\frac{i_12}{100})^{12}=104.07$ Euro, also 7 Cent mehr. Dies schaut zwar nicht nach viel aus. Wenn die Bank aber jedem seiner Kunden 4 oder 7 Cent mehr gibt und jeder Sparer nicht nur € 100, sondern sogar € 1000 oder noch mehr auf der Bank hat, wird dieser Betrag schnell sehr groß.
Aus diesem Grund gibt es eine Methode, um den passenden (=konformen) unterjährigen Zinssatz zu berechnen.
b) der konforme (äquivalente) Zinssatz
Der konforme Zinsssatz wird auch als gleichwertiger Zinssatz oder äquivalenter (=lat. gleichwertig) Zinssatz bezeichnet.Er wird verwendet, wenn während einer Zinsperiode mehrmals eingezahlt wird (z.B. jährliche Verzinsung, aber monatliche Einzahlungen)
|
Äquivalenter Aufzinsungsfaktor
Sei $r_1$ der Aufzinsungsfaktor bei jährlicher Verzinsung und $r_m$ der Aufzinsungsfaktor bei m-maliger Verzinsung innerhalb eines Jahres, dann muss folgende Gleichung gelten, damit beide Aufzinsungsfaktoren gleichwertig (konform) sind: $$r_1=(r_m)^m$$ bzw. $$ \sqrt[m]{r_1}=r_m $$ |
Herleitung und Erklärung
Es soll gelten, dass der jährliche Zinssatz gleich hoch ist wie der m-mal angewandte unterjährige ZS (insgesamt sollen in einem Jahr gleich viele Zinsen zusammenkommen)
$$K_0\cdot r_1 = K_0\cdot (r_m)^m$$
Kürzt man $K_0$, so erhält man:
$$r_1=(r_m)^m$$
bzw.
$$ \sqrt[m]{r_1}=r_m $$
Der konforme (=äquivalente) unterjährige Zinssatz $i_m$ kann dann mit der Gleichung
| $$r_m=1+\frac{i_m}{100}$$ |
bestimmt werden.
Ein Kredit wird mit 5 % p.a. verzinst. Wenn nun die ganze Schuld bereits nach einem Quartal beglichen wird, muss der konforme Quartalszinssatz berechnet werden. Bestimme diesen.
Antwort: Der Quartalszinssatz beträgt 1.23 % p.a.
Ein Kredit wird monatlich mit 2 % p.m. verzinst. Bestimme den konformen Jahreszinssatz.
Antwort: Die jährliche Verzinsung beträgt 26.82 % p.a.
Musterbeispiel 3: relativer/nomineller Zinssatz und konformer Zinssatz gemeinsam:
Ein Kredit wird nominell mit 4 % p.a. quartalsmäßig verzinst. Da die Raten monatlich eingezahlt werden, muss der konforme Monatszinssatz bestimmt werden. Berechnen Sie diesen.
$$ i_4=\frac{i}{4}=\frac{4 \textrm{ %} }{4}=1 \textrm{ % p.q.} $$
2. Schritt: Anschließend wird mithilfe des Quartalszinssatzes der konforme Monatszinssatz berechnet.
$$ (r_{12})^3=r_4 $$
$$\textrm{ Hinweis: Wenn man drei Monate verzinst (=}(r_{12})^3 \textrm{), so verzinst man insgesamt ein ganzes Quartal (=}r_4 ) $$
$$ r_{12}=\sqrt[3]{1.01} $$
$$ r_{12}=1.003322 \rightarrow i_{12}=0.003322 \textrm{ % p.m.} $$
A: Der konforme Monatszinssatz beträgt 0.3322 % p.m.
Der durchnittliche Zinssatz - geometrisches Mittel
Im Laufe der Jahre kann sich ein Zinssatz immer wieder ändern. So kann er einmal größer werden, dann wieder kleiner, usw.Hier ist es natürlich interessant zu wissen, wie groß der durchschnittliche Zinssatz $\bar{i}$ über einen bestimmten Zeitabschnitt ist.
|
Im folgenden seien $r_1,\ r_2, \ r_3,\ \dots , \ r_n$ die Aufzinsungsfaktoren für die Jahre 1 bis n. Dann gilt für den durchschnittlichen Aufzinsungsfaktor $\bar{r}$ und das Kapital nach n Jahren:
$$K_0\cdot r_1\cdot r_2\cdot r_3 \cdots r_n = K_0 \cdot \left(\bar{r}\right)^n$$ $$ r_1 \cdot r_2\cdot r_3 \cdots r_n = \cdot \left(\bar{r}\right)^n $$ $$ \sqrt[n]{r_1 \cdot r_2\cdot r_3 \cdots r_n}=\bar{r} $$ Mithilfe des durchschnittlichen Aufzinsungsfaktors kann dann einfach der durchschnittliche Zinssatz $\bar{i}$ bestimmt werden. |
Ein Kapital von € 100 wird im ersten Jahr mit 2 % p.a., im zweiten Jahr mit 4 % p.a. und im dritten Jahr mit 3.5 % p.a. verzinst.
Berechne jenen durchschnittlichen Zinssatz $\bar{i}$, mit dem das Kapital über die drei Jahre konstant verzinst werden hätte können.
2=
Die Formel für den Endwert nach drei Jahren ist
$$K_3=100\cdot 1.02\cdot 1.04\cdot 1.035=100\cdot \left(\bar{r}\right)^3 $$
wobei $\bar{r}$ der durchschnittliche Aufzinsungsfaktor ist.
Somit gilt:
$$ 1.02\cdot 1.04\cdot 1.035=\left(\bar{r}\right)^3 $$
$$\sqrt[3]{1.02\cdot 1.04\cdot 1.035}=\bar{r}$$
$$ 1.0316 = \bar{r}$$
$$\bar{i}=3.16$$
Der das Kapital wird mit einem durchschnittlichen Zinssatz von 3.16 % p.a. verzinst.
Beispiele
- Aufgaben zur Zinseszinsformel von R. Brinkmann
- ? Wichtig! Übungs-Rechner zum konformen Zinssatz
- Aufgaben zu allen Themen: siehe Trauner 2. Klasse, Buch S. 86-90