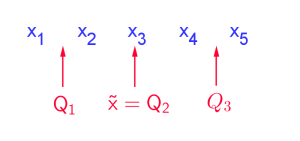Inhalt:Statistik:Streuungsmaße

Inhalt:Statistik:Streuungsmaße

Streuungsmaße - statistische Kennzahlen für die Streuung

Streuung von Daten

Im vorigen Kapitel haben wir gelernt, wie wir verschiedene Arten von Zentralmaßen bestimmen. Ein Zentralmaß allein sagt uns allerdings noch nicht viel über die Verteilung (= Streuung) der Werte aus.

In beiden Graphiken ist das arithm. Mittel $\bar{x}=1$, ....

... allerdings ist im linken Bild die Streuung der Werte eindeutig größer als im rechten Bild.

Beide Datenmengen in den Abbildungen haben denselben Mittelwert, aber unterschiedliche Streuungen. Die Werte im rechten Bild liegen näher um den Mittelwert $1$ als die Werte im linken Bild.

Aus diesem Grund lernen wir nun noch zusätzliche Kennzahlen für die Streuung von Werten kennen, um solche Datenmengen besser unterscheiden zu können.

Spannweite

Definition

Die Spannweite ist die Differenz (Abstand) zwischen dem kleinsten und dem größten Wert der Datenmenge. $$\text{Spannweite}=x_{max}-x_{min}$$

Beispiel: Gegeben sei die Datenliste $\{1;2;2;2;5\}$. Bestimme die Spannweite.

Lösung: $x_{max}=5;\ x_{min}=1$ $$\text{Spannweite}=x_{max}-x_{min}=5-1=4$$

Antwort: Die Spannweite beträgt $4$.

Varianz und Standardabweichung

Eine andere Möglichkeit, um die Streuung anzugeben wäre folgende: Wir berechnen den durchschnittlichen Abstand aller Werte vom arithmetischen Mittel $\bar{x}$. Diesen durchschnittlichen Abstand nennen wir Standardabweichung oder kurz $\sigma$ (= sigma).

Herleitung der Standardabweichung:
Um die durchschnittlichen Abstände aller Werte vom arithmetischen Mittel $\bar{x}$ (= Standardabweichung) zu erhalten, machen wir Folgendes:

$$\ $$

1. Schritt: Wir berechnen den Abstand aller Werte von $\bar{x}$:

   $$(x_1-\bar{x}) \textrm{ und } (x_2-\bar{x}) \textrm{ und ... und } (x_n-\bar{x})$$

2. Schritt: Da die Abstände mitunter negativ sind (wenn $x_i<\bar{x}$), quadrieren wir alle Abstände:

   $$(x_1-\bar{x})^2 \textrm{ und } (x_2-\bar{x})^2 \textrm{ und ... und } (x_n-\bar{x})^2$$

3. Schritt: Nun zählen wir die Quadrate aller Abstände zusammen und berechnen den Durchschnitt (d. h. wir dividieren durch $n$):

   $$\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n}$$

4. Da wir oben quadriert haben, ziehen wir nun wieder die Wurzel (Achtung: Dadurch fallen die $(\ )^2$ nicht weg!):

   $$\sqrt{\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n} }$$

Oder verkürzt angeschrieben: $$\sqrt{ \frac{\sum_{i}(x_i-\bar{x})^2}{n} }$$

Definition

Die Standardabweichung $\sigma$ ist ein Maß für die Abweichung aller Werte vom arithmetischen Mittel $\bar{x}$ und wird berechnet mit $$\sigma=\sqrt{\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n} }$$ Verkürzt: $$\sigma=\sqrt{ \frac{\sum_{i}(x_i-\bar{x})^2}{n} }$$ Die Varianz $\sigma ^2$ ist das Quadrat der Standardabweichung: $$\sigma ^2=\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n} =\frac{\sum_{i}(x_i-\bar{x})^2}{n}$$

Berechnen Sie arithmetisches Mittel und Standardabweichung der Liste $\{1;2;2;2;5\}$.

$n=5$ Werte

$$\bar{x}=\frac{1+2\cdot 3+5}{5}=\frac{12}{5}=2.4$$ Somit beträgt das arithmetische Mittel $\bar{x}=2.4$.

Um die Standardabweichung zu berechnen, ermitteln wir zuerst die Varianz und ziehen anschließend die Wurzel (so vermeiden wir häufige Rechenfehler): $$\sigma^2 =\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n}$$ $$\sigma^2=\frac{(1-2.4)^2+(2-2.4)^2+(2-2.4)^2+(2-2.4)^2+(5-2.4)^2}{5}$$ $$\sigma^2=\frac{(1-2.4)^2+(2-2.4)^2\cdot 3+(5-2.4)^2}{5}$$ $$\sigma^2=\frac{(-1.4)^2+(-0.4)^2\cdot 3+2.6^2}{5}$$ $$\sigma^2=\frac{9.2}{5}=1.84$$ Somit erhalten wir für die Standardabweichung $\sigma$: $$\sigma=\sqrt{\sigma^2}=\sqrt{1.84}=1.36$$ Die Standardabweichung beträgt $\sigma=1.36$.

Quartile

Definition

Die Quartile $Q_1,\ Q_2\,\ Q_3$ teilen die Werte der Datenmenge insgesamt in $4$ Bereiche. Quartile einer Datenmenge mit $5$ Werten. $Q_1$ ist zwischen dem 1. und 2. Wert, $Q_3$ zwischen dem 4. und 5. Berechnung: Zuerst berechnen wir den Median $Q_2$, der die Daten in zwei Hälften teilt. $Q_2$ ist gleichzeitig das zweite Quartil $Q_2$. Das erste Quartil $Q_1$ ist der mittlere Wert in der linken Hälfte. Das dritte Quartil $Q_3$ ist der mittlere Wert der zweiten Hälfte.

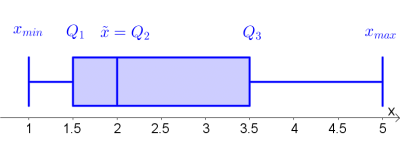
Die Quartile sind vor allem für die Erstellung eines Boxplot-Diagramms relevant.

Gegeben ist die Datenliste $\{1;2;2;2;5\}$. Bestimme $x_{min},\ x_{max}$ sowie alle Quartile und erstelle damit ein Boxplot-Diagramm.

$\ $

• $x_{min}=1$
• $x_{max}=5$
• $\{1\underbrace{;}_{Q_1}2;\ \underbrace{2}_{Q_2 }\ ;\ 2\underbrace{;}_{Q_3} 5\}$

  $Q_1=\frac{1+2}{2}=1.5$,

  $Q_2=2$ und

  $Q_3=\frac{2+5}{2}=3.5$

Boxplot-Diagramm der Liste $\{1;2;2;2;5\}$

Merke

Der Quartilsabstand ist der Abstand zwischen den Quartilen $Q_1$ und $Q_3$. $$\text{Quartilsabstand}=Q_3-Q_1$$ Graphisch entspricht dies der Länge der „Box“ im Boxplot-Diagramm.

Gegeben ist die Datenliste $\{1;2;2;2;5\}$. Bestimme den Quartilsabstand der Daten.

Aus dem obigen Beispiel wissen wir, dass $Q_1=1.5$ und $Q_3=3.5$.

Somit beträgt der Quartilsabstand $$Q_3-Q_1=3.5-1.5=2$$