Wachstums- und Zerfallsprozesse

Einleitung und Grundbegriffe
Lineares Wachstum
Exponentielles Wachstum
Unterschied: Lin. vs. Exp.
Exponentielle Abnahme
Matura-Aufgaben

In der Natur vorkommende Wachstums- und Zerfallsprozesse (z.B. Wachstum einer Bevölkerung, Zerfall eines radioaktiven Atoms, Abnahme des Alkoholspiegels) können mithilfe von mathematischen Funktionen beschrieben werden.

Für die Matura sind dabei besonders die folgenden Funktionen wichtig:

Grundbegriffe

$t...$ gibt die vergangene Zeit an (in Jahren, Tagen, Stunden oder ... . Die Einheit steht immer in der Angabe!)
$N_0...$ Anfangswert (Anzahl/Größe zum Zeitpunkt $0$)
$N(t)...$ Anzahl/Größe nach $t$ Zeiteinheiten (z. B. $t$ gebe die Stunden an, dann ist $N(5)$ die Anzahl nach $5$ Stunden)

$\rightarrow$ nächste Seite ...

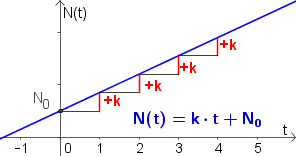
Lineares Wachstum $N(t)= k\cdot t +N_0$

Definition und Verwendung

Graph einer linearen Zunahme

Graph einer linearen Abnahme

Eine Größe verändert sich linear, wenn sie in gleichen Zeitabständen um denselben konstanten Wert $k$ wächst. Die Funktionsgleichung für eine solche Veränderung lautet dann: $$ N(t)= k\cdot t +N_0 $$

Ist $k>0$, so handelt es sich um ein lineares Wachstum
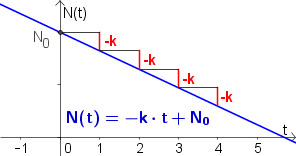
Ist $k<0$, so handelt es sich um eine lineare Abnahme

Hinweise:

Bei $$ N(t)= k\cdot t +N_0 $$ handelt es sich um eine lineare Funktion der Form

$$ y=k\cdot x+d$$

Mit der unabhängigen Variable $t=x$, der davon abhängigen Variable $N(t)=y$ und dem Startwert $N_0=d$

Herleitung der Funktionsgleichung:

Angenommen eine Population hat zu Beginn $N_0$ Individuen und wächst pro Zeiteinheit (z. B. pro Stunde) um den Wert $k$.

Dann gilt für $N(1)=$ Individuen nach einer Stunde:

$$N(1)=N_0+k$$

Nach $2$ Stunden hat sich die Population wieder um $k$ vermehrt und damit ist

$$N(2)=N(1)+k=(N_0+k)+k=N_0+2k$$

Und nach $3$ Stunden gilt

$$N(3)=N(2)+k=(N_0+2k)+k=N_0+3k$$

Ganz allgemein gilt dann für die Population nach $t$ Stunden:

$$N(t)=N_0+k\cdot t$$

Musterbeispiel:

Stanislaus hat ein Geburtsgewicht von $3120 g$. Nach $3$ Wochen hat er bereits $3900 g$.

Erstelle ein lineares Modell, welches die Abhängigkeit des Gewichts vom Alter beschreibt.
Was bedeuten die Parameter $k$ und $d$ in diesem Zusammenhang?
Stanislaus ist bei seiner Taufe $10$ Wochen alt. Welches Gewicht hat er?
Wann erreicht Stanislaus ein Gewicht von $6,2 kg$?

Lösung

$y=260x+3120$, wobei $y=$ Gewicht in $g$, $x=$ Alter in Wochen
$k$ beschreibt die wöchentliche Zunahme in Gramm und $d$ beschreibt das Geburtsgewicht von Stanislaus
$y=260\cdot 10+3120=5720$. Stanislaus wiegt nach $10$ Wochen $5720 g$.
Löse die Gleichung: $6200=260x+3120$. Lösung: $x=11,84$. Also erreicht Stanislaus in der $12.$ Woche nach der Geburt ein Gewicht von $6,2 kg$.

Übungsaufgaben

Wassertonne

Wassertonne (Lösung)

$Bifie$ : Tauchen

$\rightarrow$ nächste Seite ...

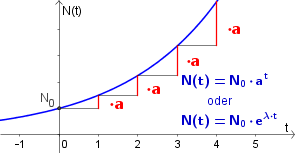
Exponentielles Wachstum $N(t)=N_0\cdot a^t$ bzw. $N(t)=N_0\cdot e^{\lambda \cdot t}$

Definition und Verwendung

Eine Größe wächst exponentiell, wenn sie in gleichen Zeitabständen um denselben konstanten Faktor $a>1$ wächst. Wie bei den Exponentialfunktionen gibt es auch hier zwei Formeln:

Graph einer exponentiellen Zunahme

$$N(t)=N_0\cdot a^t $$

$$N(t)=N_0\cdot e^{\lambda \cdot t}$$

$a>1 ...$ ist der Wachstumsfaktor und gibt an, mit welchem Faktor sich die Population pro Zeiteinheit verändert. Da die Population wächst, muss $a>1$ sein (siehe Exponentialfunktionen).

Beispiel:

$a=1.26$

$\rightarrow $

die Population wächst um den Faktor $1.26$

$\rightarrow $

die Population wächst pro Zeiteinheit um $26 \%$

$\lambda>0 ...$ ist die Wachstumsrate.

Es gilt: $a=e^\lambda $

Verdoppelungszeit

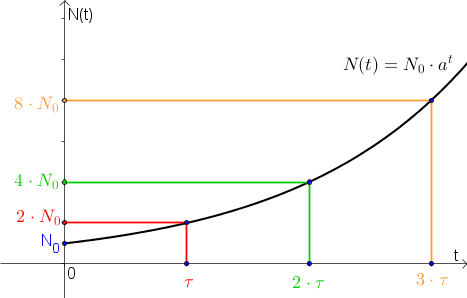
Eine besondere Eigenschaft des exponentiellen Wachstums ist, dass die Zeit für eine Verdoppelung der Anfangsgröße immer gleich groß ist (mit einer kleinen Überlegung findest du leicht heraus, dass dies schon aus der Definition des exponentiellen Wachstums folgt). Aus diesem Grund definiert man die:

Definition: Verdoppelungszeit $\tau $

Die Verdoppelungszeit $\tau$ ist die Zeit, in der sich eine Größe verdoppelt hat. Insbesondere gilt: $$N(\tau)=2\cdot N_0$$

$$\textrm{(in Worten: „die Anzahl nach $\tau$ ($=$"tau") Zeiteinheiten ist das Doppelte des Anfangswertes }N_0$$

1. Musterbeispiel: Berechnung der Verdoppelungszeit bei bekannter Anfangsmenge

Graph der Wachstumsfunktion $N(t)=350\cdot 1.065^t$

Ein Kapital auf einem Sparbuch wächst jährlich um $6.5 \%$ p. a. (d. h. $6.5 \%$-ige Verzinsung pro Jahr).

a) Bestimmen Sie die Funktionsgleichung, wenn zu Beginn $100€$ auf dem Sparbuch liegen.
b) Ermitteln Sie die Verdoppelungszeit, d. h. berechnen Sie, wann sich das Anfangskapital verdoppelt hat.
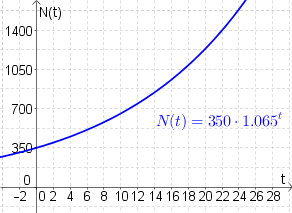
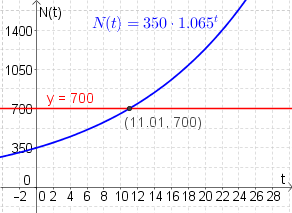
c) Die folgende Graphik gibt die Entwicklung für ein Anfangskapital von $350€$ an. Lesen Sie aus dem Graphen die Verdoppelungszeit ab.

Begründen Sie zusätzlich, warum die Verdoppelungszeit gleich groß wie in Aufgabe b) ist.

Lösung

a) $N_0=100$; $a=(1+\frac{6.5}{100})=1.065 \ \ \rightarrow$ $\underline{\underline{N(t)=100\cdot 1.065^t}}$

b)

$N_0=100$
$a=1.065$
$N(t)=200$
$t=$?

Bestimmung der Verdoppelungszeit

$$200=100\cdot 1.065^t$$ $$2=1.065^t |\log$$ $$\log 2 = t\cdot \log 1.065$$ $$\frac{\log 2}{\log 1.065}=t$$ $$\underline{\underline{t= 11.01}}$$

c) Wie anhand des Graphen zu sehen ist, beträgt die Verdoppelungszeit $11.01$ Jahre, da sich hier das Anfangskapital von $350€$ auf $700€$ verdoppelt hat.

Die Verdoppelungszeit hängt nicht vom Startwert $N_0$, sondern nur vom Wachstumsfaktor $a$ ab. Aus diesem Grund sind die Verdoppelungszeiten in b) und c) ident.

2. Musterbeispiel: Berechnung der Verdoppelungszeit bei unbekannter Anfangsmenge

Die Größe einer Bakterienpopulation nach $t$ Stunden kann mithilfe der Funktion $N(t)=N_0\cdot 1.14^t$ angegeben werden.

a) Bestimmen Sie, um wie viel Prozent sich die Population pro Stunde vergrößert.
b) Berechnen Sie die Verdoppelungszeit.

Lösung

a) $a=1.14\ \ \rightarrow\ \ 14 \%$ Wachstum pro Stunde.

b) Nach der Verdoppelungszeit ist $N(t)=2\cdot N_0$ (d. h. der Anfangswert hat sich verdoppelt). Setzen wir dies für $N(t)$ in die Funktionsgleichung, so erhalten wir: $$ N(t)=N_0\cdot 1.14^t$$ $$ 2\cdot N_0=N_0\cdot 1.14^t \ \ \ |:N_0$$ $$ 2=1.14^t \ \ \ |\log ( \ )$$ Wichtig: In der oberen Zeile hat sich das $N_0$ weggekürzt! Damit sehen wir, dass die Verdoppelungszeit unabhängig vom Startwert $N_0$ ist. Dies kam auch schon im 1. Musterbeispiel vor. $$ \log 2=t\cdot \log 1.14 $$ $$\frac{\log 2}{\log 1.14}=t$$ $$\underline{\underline{t=5.29}}$$ A: Die Verdoppelungszeit beträgt $5.29$ Stunden.

3. Musterbeispiel: Bestimmen des Wachstumsfaktors bei bekannter Verdoppelungszeit

Die Verdoppelungszeit eines exponentiellen Wachstumsprozesses der Form $N(t)=N_0\cdot a^t$ beträgt $17$ Tage ($t$ gibt die Tage an).

a) Berechnen Sie den Wachstumsfaktor $a$.
b) Bestimmen Sie die Zeit, wie lange es dauert, bis das $8$-Fache des Anfangswertes vorhanden ist.

Lösung:

a) Aus der Angabe geht hervor, dass $N(17)=2\cdot N_0$ ist. Dies setzen wir nun in die Funktionsgleichung ein: $$N(t)=N_0\cdot a^t$$ $$N(17)=N_0\cdot a^{17}$$ $$2\cdot N_0=N_0\cdot a^{17} \ \ \ |:N_0$$ $$2=a^{17} \ \ \ |\sqrt[17]{\ \ \ }$$ $$\sqrt[17]{2}=a$$ $$\underline{\underline{a=1.0416}}$$ A: Der Wachstumsfaktor $a$ beträgt $1.0416$, womit pro Tag $4.16 \%$ dazu kommen.

b) Aus der Angabe wissen wir, dass es nach $17$ Tagen zu einer Verdoppelung gekommen ist. Da sich das exponentielle Wachstum in gleichen Zeitabständen um denselben Faktor vermehrt, gilt:

nach $2\cdot 17=34$ Tagen kommt es zu einer Vervierfachung ($2\cdot 2=4$).
Nach $3\cdot 17=51$ Tagen kommt es zu einer Verachtfachung. ($2\cdot 2 \cdot 2=8$)

Somit dauert es $51$ Tage. Schau dir dazu auch den Graphen bei der unteren Bemerkung an!

Merke:

Die Verdoppelungszeit wird berechnet, indem man für $N(t)=2\cdot N_0$ einsetzt.

Die Verdoppelungszeit ist unabhängig vom Anfangswert $N_0$ (vgl. 2. Musterbeispiel)

Mehrfache Verdoppelung eines exponentiellen Wachstums

$\rightarrow$ nächste Seite ...

Unterschied: Lineares und Exponentielles Wachstum

Es ist wichtig, die Unterschiede zwischen dem linearen und dem exponentiellen Wachstum zu kennen. Aus diesem Grund vergleichen wir hier die beiden Wachstumsprozesse:

Lineares Wachstum	Exponentielles Wachstum
Addition um eine konstante Zahl	Multiplikation um einen konstanten Faktor
immer $+k$	immer $\cdot a$
Graph ist eine Gerade	Graph ist eine exponentielle Kurve
wächst immer um dieselbe konstante Zahl $k$	wächst immer schneller
Graph einer linearen Zunahme	Graph einer exponentiellen Zunahme

Übungsbeispiel: linear oder exponentiell?

Ordne dem passenden Wachstum zu und bestimme $k$ bzw. $a$:

Der Umfang eines Baumes nimmt jährlich um $5 \%$ zu:
Der Meeresspiegel steigt jährlich um $4 cm$:
Die Bevölkerung wächst jährlich um den Faktor $1.2$:
Der Stamm eines Baumes wird pro Jahr um $1 cm$ dicker:
Ein Kapital wird jährlich mit $3 \%$ p. a. verzinst.
Der Umsatz eines Betriebes sinkt jährlich um $12 \%$.

Lösung:

Der Umfang eines Baumes nimmt jährlich um $5 \%$ zu: exponentiell mit $a=1.05$
Der Meeresspiegel steigt jährlich um $4 cm$: linear mit $k=4 cm$
Die Bevölkerung wächst jährlich um den Faktor $1.2$: exponentiell mit $a=1.2$
Der Stamm eines Baumes wird pro Jahr um $1 cm$ dicker: linear mit $k=1 cm$
Ein Kapital wird jährlich mit $3 \%$ p. a. verzinst. exponentiell mit $a=1.03$
Der Umsatz eines Betriebes sinkt jährlich um $12 \%$: exponentiell mit $a=0.88 \rightarrow$ siehe exponentielle Abnahme

$\rightarrow$ nächste Seite ...

Exponentielle Abnahme $N(t)=N_0\cdot a^t$ oder $N(t)=N_0\cdot e^{-\lambda\cdot t}$

Definition:

Von einer exponentiellen Abnahme spricht man, wenn sich eine Größe in gleichbleibenden Zeitintervallen immer um den gleichen Faktor verkleinert.

Graph einer exponentiellen Abnahme

$$N(t)=N_0\cdot a^t $$

$$N(t)=N_0\cdot e^{-\lambda \cdot t}$$

$a<1 ...$ ist der Abnahmefaktor und gibt an, mit welchem Faktor sich die Population pro Zeiteinheit verringert. Da die Population abnimmt, muss $0<a<1$ sein (siehe Exponentialfunktionen)

Beispiel:

$a=0.64$

$\rightarrow $

die Population verringert sich um den Faktor $0.64$

$\rightarrow $

die Population verringert sich pro Zeiteinheit um $1-0.64=0.36=36 \%$

$-\lambda<0 ...$ ist die Abnahmerate

Es gilt: $a=e^{-\lambda} $

Halbwertszeit

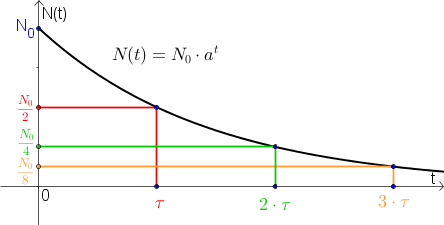
Eine besondere Eigenschaft der exponentiellen Abnahme ist, dass die Zeit für eine Halbierung der Anfangsgröße, immer gleich groß ist (vgl. Verdoppelungszeit beim exponentiellen Wachstum). Aus diesem Grund definiert man die:

Definition: Halbwertszeit $\tau $

Die Halbwertszeit $\tau$ ist die Zeit, in der sich eine Größe halbiert hat. Insbesondere gilt: $$N(\tau)=\frac{N_0}{2}$$

$$\textrm{(in Worten: „die Anzahl nach $\tau$ Zeiteinheiten ist die Hälfte des Anfangswertes }N_0\textrm{"}$$

Musterbeispiel:

Von einer bestimmten Menge eines radioaktiven Elements zerfallen stündlich $4 \%$.

a) Stellen Sie das Zerfallsgesetz in der Form $N(t)=N_0\cdot a^t$ auf.
b) Bestimmen Sie die Halbwertszeit.
c) Bestimmen Sie zusätzlich noch das Zerfallsgesetz in der Form $N(t)=N_0\cdot e^{-\lambda \cdot t}$
d) Nach wie vielen Stunden ist nur noch $1 \%$ der Anfangsmenge vorhanden?

Lösung:

a) $a=0.96 \rightarrow $ Somit lautet das Zerfallsgesetz: $$ N(t)=N_0\cdot 0.96^t$$

b) Bei der Halbwertszeit gilt, dass $N(t)=\frac{N_0}{2}$ ist. Setzt man dies in das Zerfallsgesetz ein, erhält man: $$ N(t)=N_0\cdot 0.96^t$$ $$ \frac{N_0}{2}=N_0\cdot 0.96^t \ \ \ |:N_0$$ $$\frac{1}{2}=0.96^t\ \ \ |\ln $$ $$ \ln \frac{1}{2}=t\cdot \ln 0.96 $$ $$\frac{\ln \frac{1}{2}}{\ln 0.96}=t$$ $$\underline{\underline{t=16.98}}$$

A: Die Halbwertszeit beträgt ca. $17$ Stunden.

c) Hier müssen wir nur das $\lambda$ berechnen. Es gilt $a=e^{-\lambda}$. Dadurch kann $\lambda$ bestimmt werden: $$0.96=e^{-\lambda}$$ $$ \ln 0.96 = -\lambda \ln e \ \ \ |\ln e=1$$ $$-\ln 0.96=\lambda$$ $$ \underline{\underline{0.041=\lambda}}$$

Somit lautet das Zerfallsgesetz in der $e^{-\lambda}$-Form: $$N(t)=N_0\cdot e^{-0.041\cdot t}$$

d) Gefragt ist, wann $$N(t)=1 \textrm{% von }N_0$$ ist. Formulieren wir dies noch "mathematischer", so erhalten wir: $$N(t)=0.01\cdot N_0$$ Setzen wir dies in das Zerfallsgesetz aus a) oder c) ein (es ist hier völlig egal, welche Formel man nimmt), so erhält man: $$N(t)=N_0\cdot e^{-0.041\cdot t}$$ $$0.01\cdot N_0=N_0\cdot e^{-0.041\cdot t}$$ $$0.01=e^{-0.041\cdot t} | \ln \textrm{ und } \ln e=1$$ $$\ln 0.01=-0.041\cdot t$$ $$\frac{\ln 0.01}{-0.041}=t$$ $$\underline{\underline{t=112.32}}$$

A: Erst nach etwas mehr als $112$ Stunden sind $99 \%$ der Anfangsmenge zerfallen.

Merke: $\ \ \ \ \ \ $