Differenzen- und Differentialquotient
- Was lernst du hier
- Der Differenzenquotient (= durchschnittliche Steigung)
- Der Differentialquotient (= momentane Steigung, $f'$)
- Differentialquotient ist 1. Ableitung
- Graphisches Bestimmen von $f'$
- Rechnerisches Bestimmen von $f'$ - Ableitungsregeln
- Grundlegende Regeln
- Vertiefende Regeln zur Ableitung zusammengesetzter Funktionen
- Lernvideos
- Interaktive Übungen
- Änderungsmaße
- Matura-Aufgaben
Inhaltsverzeichnis
Der Differenzenquotient
Definition
|
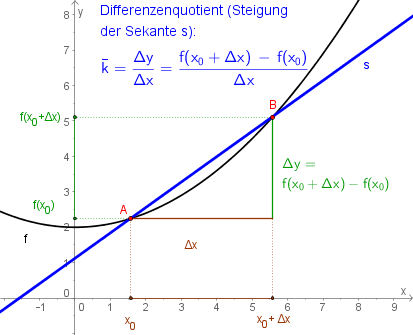
Die durchschnittliche Änderungsrate einer Funktion $f$:
$$ \bar{k}=\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{(x+\Delta x)- x} $$ wird als Differenzenquotient bezeichnet. Er gibt die Steigung der Sekante durch die Punkte $A=(x \vert f(x))$ und $B=(f(x+\Delta x) \vert x+\Delta x )$ an (siehe Abbildung rechts). |
Bemerkungen:
- $\Delta$ (= Delta (4. Buchstabe im griechischen Alphabet)) steht für „Unterschied“. $\Delta x$ ist der Unterschied auf der $x$-Achse, $\Delta y$ der Unterschied auf der $y$-Achse.
- Wie aus der rechten Abbildung hervorgeht, ist $\frac{\Delta y}{\Delta x}=\frac{\textrm{Höhenunterschied}}{\textrm{Längenunterschied}}$
- Der Name Differenzenquotient kommt daher, dass er aus dem Quotienten (= Ergebnis einer Division) zweier Differenzen (= Ergebnis einer Subtraktion) entsteht:
$$ \bar{k}=\frac{f(x+\Delta x)-f(x)}{(x+\Delta x)-\Delta x} $$
- $Aha!$ Hier findest du ein Arbeitsblatt zum Differenzenquotienten
Video-Erklärung
| Video zum Differenzenquotienten | ||
|---|---|---|
Hinweise zum Video:
$$ \textrm{Steigung}=\textrm{Geschwindigkeit} $$ | ||
|
| ||
Aufgaben
| ||
Lösungen
|
Beispiele
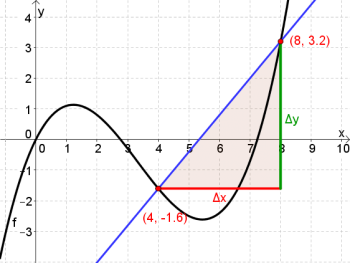
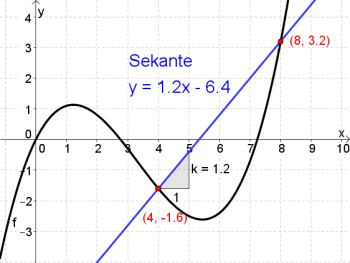
Gegeben ist die Funktion $f$ mit $f(x)=0.1x³ - x² + 2x$.
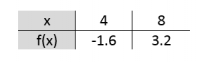
a) Berechnen Sie den Differenzenquotienten im Intervall $[4,8]$.
b) Stellen Sie diesen auch graphisch in einem Koordinatensystem mit dem Graphen der Funktion $f$ dar.
Zuerst machen wir eine Wertetabelle :
Nun setzen wir ein: $$\bar{k}_{[4,8]}=\frac{\Delta y}{\Delta x}=\frac{f(8)-f(4)}{8-4}=\frac{3.2-(-1.6)}{8-4}=\frac{4.8}{4}=\underline{\underline{1.2} }$$
b) Der Differenzenquotient ist die Steigung der Sekante durch die beiden Punkte $(4\vert -1.6)$ und $(8\vert 3.2)$.
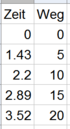
Der zurückgelegte Weg eines anfahrenden Fahrzeuges entlang der Zeit kann mithilfe der quadratischen Funktion $s$ mit $s(t)=0.1\cdot t^2$ beschrieben werden.
$t...$ Zeit in Sekunden ($s$) (es gilt: $t\geq 0$)
$s(t)...$ Weg in Metern ($m$)
a) Berechnen Sie den Weg, den das Fahrzeug nach $5 s$ zurückgelegt hat.
b) Ermitteln Sie, nach wie vielen Sekunden das Fahrzeug $8.1 m$ weit gefahren ist.
c) Berechnen Sie die durchschnittliche Geschwindigkeit zwischen der $5.$ und $9.$ Sekunde in $km/h$.
$$s(t)=0.1\cdot t^2$$
$$s(5)=0.1\cdot 5^2=2.5\ m$$
A: Nach $5$ Sekunden hat das Fahrzeug einen Weg von $2.5 m$ zurückgelegt.
b) $s(t)=8.1 m$ und gesucht ist das passende $t$:
$$s(t)=0.1\cdot t^2$$
$$8.1=0.1\cdot t^2$$
$$81=t^2$$
$$\pm 9=t$$
A: Da die negative Lösung nicht infrage kommt (das Auto fährt an, somit betrachten wir nur positive Werte für die Zeit), hat das Fahrzeug nach $9 s$ eine Distanz von $8.1 m$ erreicht.
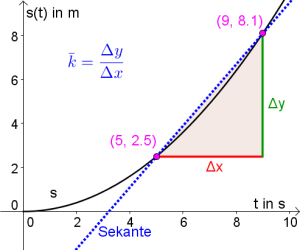
c) Die durchschnittliche Geschwindigkeit zwischen der $5.$ und $9.$ Sekunde entspricht der durchschnittlichen Steigung des Graphen von $s(t)$ im Intervall $[5;9]$ (siehe Abbildung rechts).
Die durchschnittliche Steigung kann mit dem Differenzenquotienten berechnet werden: $$\bar{k}_{[5;9]}=\frac{\Delta y}{\Delta x}=\frac{s(9)-s(5)}{9-5}\underbrace{=}_{\textrm{siehe a) und b)} } \frac{8.1-2.5}{9-5}=\frac{5.6}{4}=1.4\textrm{ m/s}$$
ACHTUNG: Da wir beim Differenzenquotient die Meter (= im Zähler) durch die Sekunden (= im Nenner) dividiert haben, erhalten wir als Einheit "Meter pro Sekunde" ($m/s$).
Laut Angabe sind aber $km/h$ gefordert, somit wandeln wir noch um: $$ 1.4\ m/s \underbrace{=}_{:1000}0.0014\ km/s \underbrace{=}_{\cdot 60\ \textrm{min}\cdot 60\ \textrm{sek} }5.04\ km/h$$ (Alternativ hätten wir die $1.4 m/s$ einfach mit $3.6=\frac{60\cdot 60}{1000}$ multiplizieren können.)
Somit hat das Fahrzeug zwischen der $5.$ und $9.$ Sekunde eine durchschnittliche Geschwindigkeit von $5.04 km/h$.
Beispiel zum Differenzenquotienten
Der Differentialquotient
Im oberen Abschnitt haben wir uns überlegt, wie wir die durchschnittliche Steigung in einem vorgegebenen Intervall bestimmen können. Dies gelang uns mithilfe des Differenzenquotienten.
Nun überlegen wir uns, wie wir die momentane Steigung an einem bestimmten Punkt berechnen können. Dies wird uns nämlich der sogenannte Differentialquotient liefern.
Definition
|
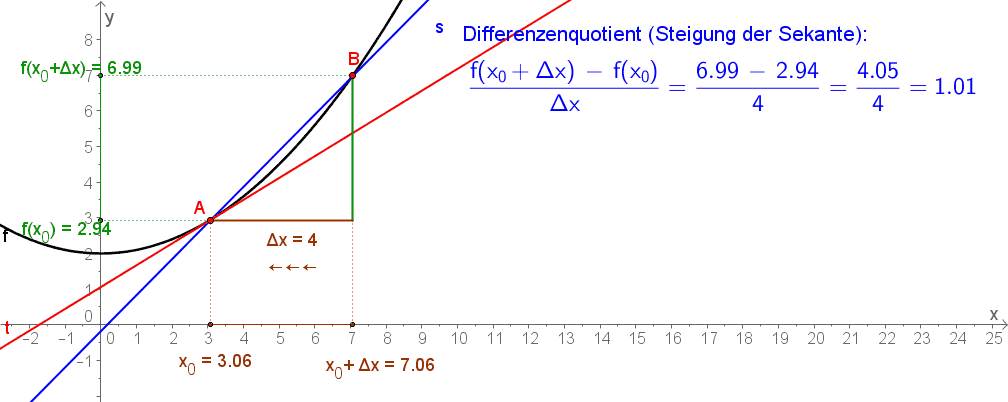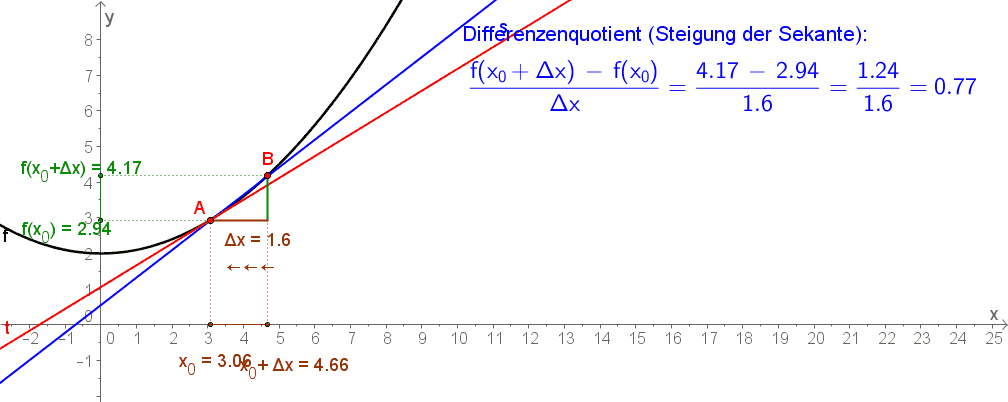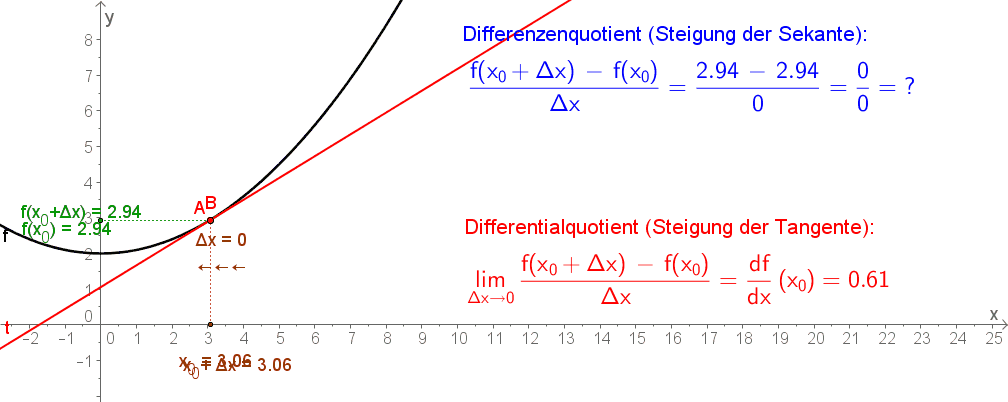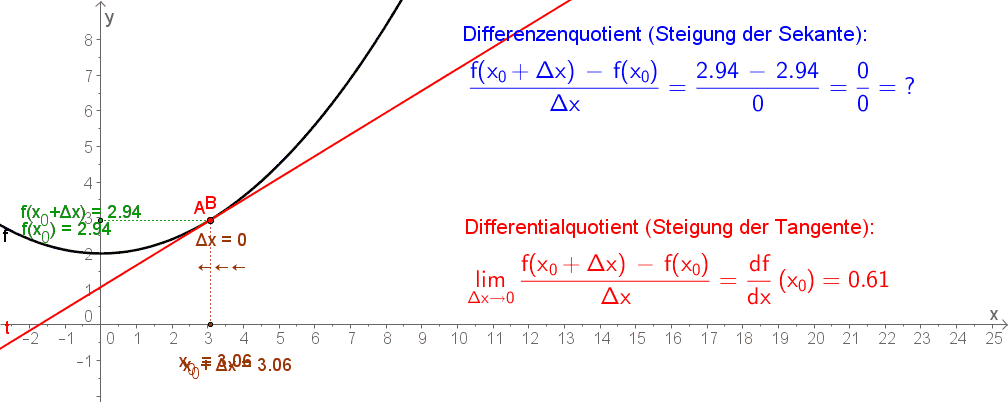
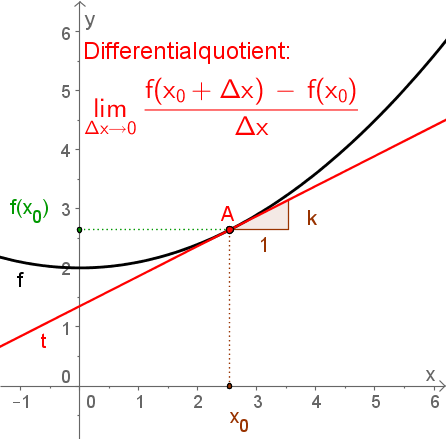
Die momentane Änderungsrate einer Funktion $f$ an der Stelle $x$
$$ {k}=\lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{(x+\Delta x)- x} $$
wird als Differentialquotient bezeichnet.
|
Bemerkungen:
- Der Ausdruck $\lim_{\Delta x \rightarrow 0} $ bedeutet, dass der Abstand auf der $x$-Achse der beiden Punkte $A$ und $B$ immer näher gegen $0$ gehen soll. An der unteren Abbildung erkennst du, dass sich dadurch die Sekante (blau) immer mehr der Tangente (rot) nähert.
- $Aha!$ $\ $ Klicke hier um zu einem interaktiven Applet zum Differenzenquotienten zu gelangen.
- Anstelle von $k$ wird auch $f'(x)$ geschrieben und damit gilt:
$$ {f'(x)}=\lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{(x+\Delta x)- x} $$
Video-Erklärung
Hinweise zum Video:
- Dieses Video ist die Fortsetzung des ersten Videos zum Differenzenquotienten.
- Anstelle von $\bar{k}$ wird hier $m$ für die Steigung verwendet.
- WICHTIG: Die Steigung in einem solchen Zeit-Weg-Diagramm ist immer die Geschwindigkeit.
$ \textbf{Steigung = Geschwindigkeit} $
Aufgaben
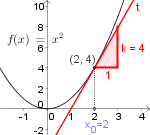
- Bestimme mithilfe des Differentialquotienten die momentane Steigung $f'(x)=k$ der Funktion $f(x)=x^2$ an der Stelle $x$.
- Bestimme mithilfe des Differentialquotienten die momentane Steigung der Funktion $f(x)=x^2$ an der Stelle $x=2$.
Lösungen
- 1. Bestimmen der momentanen Steigung $f'(x)$
$\begin{align} f'(x)=\lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{(x+\Delta x)-x}\\ f'(x)=\lim_{\Delta x \rightarrow 0} \frac{(x+\Delta x)^2-x^2}{(x+\Delta x)-x}\\ f'(x)=\lim_{\Delta x \rightarrow 0} \frac{(x^2+2\cdot x\cdot \Delta x+ \Delta x^2)-x^2}{\Delta x}\\ f'(x)=\lim_{\Delta x \rightarrow 0} \frac{2\cdot x\cdot \Delta x+ \Delta x^2}{\Delta x}\\ f'(x)=\lim_{\Delta x \rightarrow 0} \frac{\Delta x(2\cdot x+ \Delta x)}{\Delta x}\\ f'(x)=\lim_{\Delta x \rightarrow 0} \frac{(2\cdot x+ \Delta x)}{1}\\ f'(x)=\lim_{\Delta x \rightarrow 0} 2\cdot x+ \underbrace{\Delta x}_{\rightarrow 0}\\ f'(x)= 2\cdot x \end{align}$
- 2. Bestimmen der momentanen Steigung bei $x=2$:
$$f'(x)=2x$$
$$f'(2)=2\cdot 2$$
$$f'(2)=4$$
Die Steigung der Funktion an der Stelle $x=2$ beträgt $4$.
1. Ableitung $f'$
|
Die Ableitungsfunktion $f'(x)$ ist der sogenannte Differentialquotient von $f(x)$
$$ f'(x)={k}=\lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{(x+\Delta x)- x} $$ und gibt die momentane Steigung der Funktion $f$ an der Stelle $x$ an.
|

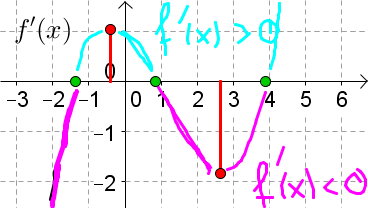
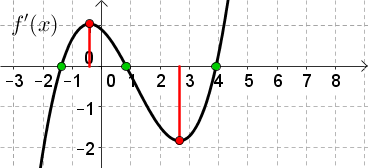
Graphisches Bestimmen von $f'$
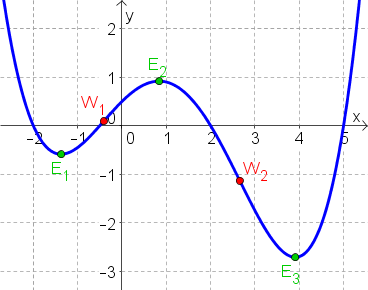
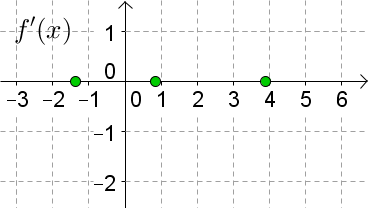
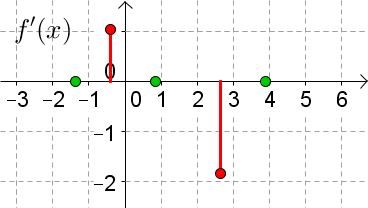
Die Ableitungsfunktion $f'(x)$ kann allein durch Betrachtung der ursprünglichen Funktion $f(x)$ graphisch bestimmt werden.
Das folgende Applet zeigt dir den Zusammenhang zwischen einer Funktion und ihrer Ableitungsfunktion. Verschiebe dazu den Punkt $P$ in der linken Graphik:
Aufgaben zu diesem Applet
1. Verschieben Sie den Punkt $P$. Auf der rechten Graphik wird laufend die Steigung $k$ beim jeweiligen $x$-Wert von $P$ abgetragen. Verschieben Sie $P$ solange, bis in der rechten Graphik ein schöner Funktionsgraph zu sehen ist. Dieser Graph ist der Graph von $f'(x)$ (=1. Ableitung von $x$).
2. Geben Sie eine andere Funktion im Eingabefeld ein. Versuchen Sie den Graphen von $f'(x)$ zuerst zu erraten und zeichnen Sie ihn erst dann durch Verschieben des Punktes $P$.
Funktionen zum Eintippen:
a) $f(x)=1.5x^3-4x^2$
b) $f(x)=0.05x^4-0.225x^3-0.325x^2+0.9x+0.5$
c) $f(x)=3x$
|
$f'(x)$ gibt die Steigung von $f(x)$ an. Somit muss gelten: |
| $f(x)$ | $f'(x)$ |
|---|---|
| 1. $f(x)$ hat bei $a$ eine Extremstelle | $\rightarrow$ Hier ist die Steigung $f'(a)=0$ |
| 2. $f(x)$ hat bei $b$ einen Wendepunkt | $\rightarrow$ Hier ist der Graph lokal am steilsten oder am flachsten $\rightarrow$ die Steigung $f'$ hat hier einen Hoch- oder Tiefpunkt $\rightarrow$ $f''(b)=0$ |
| 3. $f(x)$ ist monoton wachsend | $\rightarrow$ $f'(x)$ ist positiv, d. h. oberhalb der $x$-Achse. |
| 4. $f(x)$ ist monoton fallend | $\rightarrow$ $f'(x)$ ist negativ, d. h. unterhalb der $x$-Achse. |
Skizzieren Sie zum gegebenen Graphen von $f(x)$ den Graphen von $f'(x)$.
Überprüfe dein Wissen
- $f(x)$ und $f'(x)$ - Graphen zuordnen (LearningApps)
Rechnerisches Bestimmen von $f'$ - Ableitungsregeln
Im Folgenden sind Regeln aufgelistet, mit der $f'(x)$ berechnet werden kann.
Allgemeine Regeln
| Regel | $f(x)$ | $f'(x)$ | Bemerkung |
|---|---|---|---|
| Potenzregel | $x^n$ | $n\cdot x^{n-1}$ | Der Exponent kommt herunter, dann wird die Hochzahl um $1$ vermindert. |
| Konstantenregel
$c\in \mathbb{R}$ |
$c$ | $0$ | Konstante Funktionen haben die Steigung $= 0$. |
| Faktorregel
$a\in \mathbb{R}$ |
$a\cdot f(x)$ | $a\cdot f'(x)$ | Ein konstanter Faktor ist von der Ableitung nicht betroffen. |
| Summenregel | $f(x)+g(x)$ | $f'(x)+g'(x)$ | Eine Summe wird abgeleitet, indem jeder einzelne Summand einzeln abgeleitet wird. |
| $e$-Funktion | $e^x$ | $e^x$ | Die besondere Eigenschaft von $e^x$ ist, dass es durch Ableiten nicht verändert wird.
(d. h. Funktionswert bei $x$ = Steigung bei $x$) |
| Logarithmus | $ln|x|$ | $\frac{1}{x}$ | |
| Trigonometrische Funktionen | $\sin(x)$ $\cos(x)$ |
$\cos(x)$ $-\sin(x)$ |
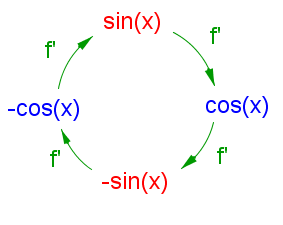 Durch mehrmaliges Ableiten der Sinus- oder Cosinusfunktion kommt man immer wieder zur Ausgangsfunktion zurück. In diesem Arbeitsblatt findest du eine Begründung dafür. |
Bestimme zu den folgenden Funktionen die Ableitungsfunktion:
- $f(x)=x^3$
- $f(x)=4x$
- $f(x)=3$
- $f(x)=5\cdot x^2$
- $x^3+5x^2-4x+3$
- $x+\frac{1}{x}-\frac{1}{x^3}+\sqrt[5]{x^2}$
- $f(x)=\frac{x^4}{5}+2\cdot e^x-ln\vert x\vert $
- $f(x)=x^3 \rightarrow f'(x)\underbrace{=}_{Potenzregel} 3\cdot x^{3-1}=3\cdot x^2$
- $f(x)=4\cdot x=4\cdot x^1 \rightarrow f'(x)\underbrace{=}_{Potenzregel} 4\cdot 1\cdot x^{1-1}=4\cdot x^0=4\cdot 1=4$
- $f(x)=3 \rightarrow f'(x)\underbrace{=}_{Konstantenregel} 0$
- $f(x)=5\cdot x^2\rightarrow f'(x)\underbrace{=}_{Faktorregel}5\cdot (x^2)' \underbrace{=}_{Potenzregel}=5\cdot 2\cdot x^{2-1}=10\cdot x$
- $x^3+5x^2-4x+3\rightarrow f'(x)\underbrace{=}_{Summenregel}(x^3)'+(5x^2)'-(4x)'+(3)' \underbrace{=}_{Potenzregel}3x^2+10x-4+0$
- $x+\frac{1}{x}-\frac{1}{x^3}+\sqrt[5]{x^2}\underbrace{=}_{umformen} x+x^{-1}-x^{-3}+x^{\frac{2}{5} }$
$$\rightarrow f'(x)\underbrace{=}_{Potenzregel}1\cdot x^0+(-1)\cdot x^{-2}-(-3)\cdot x^{-4}+\frac{2}{5}\cdot x^{(\frac{2}{5}-1)}=$$ $$=1-x^{-2}+3\cdot x^{-4}+\frac{2}{5}\cdot x^{-\frac{3}{5} }$$ $$=1-\frac{1}{x^2}+\frac{3}{x^4}+\frac{2}{5\sqrt[5]{x^3} }$$
- $f(x)=\frac{x^4}{5}+2\cdot e^x-ln \vert x \vert \rightarrow f'(x)\underbrace{=}_{Potenzregel/Faktorregel,\ e-\ und\ ln-Regel}\frac{4x^3}{5}+2\cdot e^x-\frac{1}{x}$
Weitere Übungen
Ordne im folgenden Applet Funktionen und ihre Ableitungen zu.
Produktregel
Im Gegensatz zur Summe zweier Funktionen $( f(x)+g(x))'=f'(x)+g'(x)$, siehe oben 'Summenregel'$)$ kann man das Produkt zweier Funktionen $f(x)\cdot g(x)$ nicht mehr so einfach ableiten. Hierfür braucht es die sogenannte ...
|
Produktregel
$$(f(x)\cdot g(x))'=f'(x)\cdot g(x)+f(x)\cdot g'(x)$$ „Zuerst den ersten Faktor ableiten, den zweiten stehen lassen, $$\textrm{Plus}$$ den ersten Faktor stehen lassen, den anderen ableiten.“ |
Gegeben ist die Funktion $h(x)=(x^2-1)\cdot (3x^2-4x+1)$. Bestimmen Sie $h'(x)$.
$$h(x)=\underbrace{(x^2-1)}_{f(x)} \cdot \underbrace{(3x^2-4x+1)}_{g(x)}$$ Zuerst berechnen wir in einer Nebenrechnung die Ableitungen der Faktoren: $$f(x)=x^2-1\rightarrow f'(x)=2x$$ $$g(x)=3x^2-4x-+1\rightarrow g'(x)=6x-4$$
Nun setzen wir die Formel zusammen: $$h'(x)=\underbrace{2x}_{f'(x)}\cdot \underbrace{(3x^2-4x+1)}_{g(x)}+\underbrace{(x^2-1)}_{f(x)}\cdot \underbrace{(6x-4)}_{g'(x)}$$
Zuletzt vereinfachen wir noch das Ergebnis: $$h'(x)=6x^3-8x^2+2x+6x^3-4x^2-6x+4$$ $$\underline{\underline{h'(x)=12x^3-12x^2-4x+4} }$$
Quotientenregel
Um die Ableitung einer Division von $2$ Funktionen (= Quotienten) zu berechnen, verwendet man die ...
|
Quotientenregel
$$h(x)=\frac{f(x)}{g(x)}\ \rightarrow \ h'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{(g(x))^2 }$$ Im Zähler steht bis auf das $Minus$ die Produktregel. Im Nenner wird die Nenner-Funktion quadriert. |
Bestimmen Sie die Ableitung von $h(x)=\frac{x^2-x}{x+1}$.
- Zähler: $f(x)=x^2-x\ \rightarrow f'(x)=2x-1$
- Nenner: $g(x)=x+1\ \rightarrow g'(x)=1$
Nun setzen wir die Quotientenregel zusammen: $$h'(x)=\frac{(2x-1)\cdot (x+1)-(x^2-x)\cdot 1 }{(x+1)^2}$$ $$h'(x)=\frac{2x^2+x-1-x^2+x}{x^2+2x+1}$$ $$h'(x)=\frac{x^2+2x-1}{x^2+2x+1}$$
Kettenregel
Um Klammerausdrücke oder verkettete Funktionen wie zum Beispiel $f(x)=\sqrt[3]{x^2-1}$ oder $e^{2x-1}$ abzuleiten, verwenden wir die ...
|
Kettenregel
$$h(x)=f[g(x)]\ \ \rightarrow \ \ h'(x)=\underbrace{f'(g(x))}_{\textrm{äußere Ableitung} } \cdot \underbrace{g'(x)}_{\textrm{innere Ableitung} }$$ $f(x)$ wird als äußere Funktion, $g(x)$ als innere Funktion bezeichnet. |
Gegeben ist $h(x)=\sqrt[3]{x^2-1}$. Bestimmen Sie $h'(x)$.
$$h(x)=(x^2-1)^{\frac{1}{3} }$$
- Die äußere Funktion ist nun $f(x)=(\ \ )^{\frac{1}{3} }$. Damit ist $f'(x)=\frac{1}{3}\cdot (\ \ )^{\frac{1}{3}-1}=\frac{1}{3}\cdot (\ \ )^{-\frac{2}{3} }$
- Die innere Funktion ist $g(x)=x^2-1$. Damit ist $g'(x)=2x$.
Nun setzen wir die Kettenregel zusammen: $$ h'(x)=\underbrace{\frac{1}{3}\cdot (x^2-1)^{-\frac{2}{3} } }_{\textrm{äußere Ableitung} } \cdot \underbrace{2x}_{\textrm{innere Ableitung} }$$
$$ h'(x)=\frac{2x}{3\cdot \sqrt[3]{(x^2-1)^2} }$$
Bestimmen Sie die Ableitungsfunktion von $f(x)=e^{2x-1}$.
- Die äußere Funktion ist die Exponentialfunktion $f(x)=e\textrm{^}\ \rightarrow\ f'(x)=e\textrm{^}$.
- Die innere Funktion ist $g(x)=2x-1 \ \rightarrow g'(x)=2$.
Nun setzen wir die Kettenregel wieder zusammen:
$$ h'(x)=\underbrace{e^{2x-1} }_{\textrm{äußere Ableitung} } \cdot \underbrace{2}_{\textrm{innere Ableitung} }$$ $$h'(x)=2\cdot e^{2x-1} $$
| Produkt-, Quotienten- und Kettenregel | Ableitung der Exponentialfunktion |
|---|---|
Quiz: Einfache Regeln des Differenzierens (AN 2.1)
Quiz: Begriff Ableitungsfunktion/Stammfunktion (AN 3.1)
Quiz: Grafischer Zusammenhang zwischen Funktion und Ableitungsfunktion (AN 3.2)
Matura-Aufgaben
- $Bifie$: Beleuchtungsstärke (schwer-mittel-schwer)
- Welche Inhalte brauchst du hier noch: indirekte Proportion
- $Bifie$ : Bungeejumping (leicht-mittel-mittel)
- Hier werden Ableitungsregeln benötigt.
- $Bifie$ : Leistungskurve
- Hier musst du die Ableitungsfunktion graphisch bestimmen.
- $Bifie$ : Bevölkerungswachstum in den USA (leicht-leicht-mittel)
- Siehe für Aufgabe a) auch Wachstums- und Zerfallsprozesse
- $Bifie$: Energieverbrauch beim Joggen (mittel)
- Welche Inhalte brauchst du hier noch: exponentielle Abnahme und Integration