Logarithmus

Logarithmus

Der Logarithmus ermöglicht es uns, den Exponenten frei zu stellen.

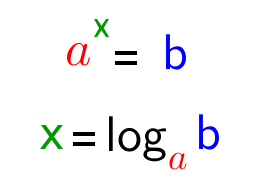
Den Logarithmus brauchen wir, um Gleichungen der Form $a^x=b$ nach x auflösen zu können.

Der Logarithmus ist der Exponent

Der Logarithmus ist eigentlich nur eine Bezeichnung für den Exponenten (Hochzahl) einer bestimmten Basis a, mit dem eine bestimmte Zahl b berechnet wird:

$$\color{red}{a}^{\color{green}{x}}=\color{blue}{b} $$ dann heißt $$\color{green}{x}=\log_{\color{red}{a}} \color{blue}{b}$$ $$\textrm{ausgesprochen: }"\color{green}{x}\ ist\ der\ Logarithmus\ zur\ \color{red}{Basis\ a}\ \color{blue}{von\ b} "$$

Beispiele

• $2^x=8 \ \rightarrow \ x=\log_2 8 $ ("x ist der Logarithmus zur Basis 2 von 8") und natürlich gilt $x=3$ da $2^3=8$.
• $5^x=25 \rightarrow \ x=\log_5 25 $ ("x ist der Logarithmus zur Basis 5 von 25") und natürlich gilt $x=2$ da $5^2=25$ ist.

Merke

Der Logarithmus zur Basis $a$ von der Zahl $b$ ist die Bezeichnung für den Exponenten. D.h. $$x=\log_a b \Leftrightarrow a^x=b$$

Berechnung mithilfe der Potenzregeln

Mithilfe der Potenzregeln und der Äquivalenz $x=log_a b \Leftrightarrow a^x=b$ lassen sich einfache Logarithmen bestimmen:

Beispiele

• $\log_5 125=\log_5 5^3 =3 \ \ \ \ \ \ \ \ $ weil $5^3=125 $
• $\log_2 16 = log_2 2^4 = 4\ \ \ \ \ \ \ \ \ \ \ $ weil $2^4=16 $
• $\log_3 \frac{1}{9}= \log_3 9^{-1}=\log_3 (3^2)^{-1}=\log_3 3^{-2}=-2\ \ \ \ \ \ \ \ $ weil $3^{-2}=\frac{1}{9} $
• $\log_{16} 4 = \log_{16} \sqrt{16}=\log_{16} 16^{\frac{1}{2} }=\frac{1}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ weil $16^{\frac{1}{2} }=4 $

Zwei besondere Basen

Besonders zwei Basen spielen bei der Berechnung mit Technogie eine große Rolle:

$\lg$ - Logarithmus zur Basis 10

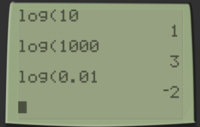
Der Logarithmus generalis (kurz $\lg$) ist der Logarithmus zur Basis 10. Im Taschenrechner ist dies die Taste $[LOG]$.$$lg=\log_{10}=[LOG]$$

Berechnung des Zehnerlogarithmus mit GeoGebra Berechnung des Zehnerlogarithmus mit dem Ti

Beispiele:

• $\lg(10)$

• $\lg(1000)=3$

• $\lg(0.01)=-2$

$\ln$ - Logarithmus zur Basis $e$

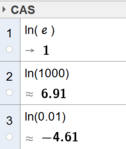
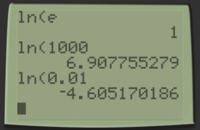
Der Logarithmus naturalis (=natürlicher Logarithmus, kurz $\ln$) ist der Logarithmus zur Basis $e$, wobei $e=2.718...$ die berühmte Eulersche Zahl ist. Im Taschenrechner findet sich die $[Ln]$-Taste direkt unter der Taste für den Zehnerlogarithmus $[LOG]$. $$\ln=\log_e=Ln$$

Berechnung des natürlichen Logarithmus mit GeoGebra Berechnung des natürlichen Logarithmus mit dem Ti

Beispiele:

• $\ln(e)=1$

• $\ln1000)=6.91$

• $\ln(0.01)=-4.61$

Rechenregeln des Logarithmus

Mithilfe der Rechenregeln für Potenzen kommt man auf die folgenden Regeln für den Logarithmus:

Regel	Formal	Begründung und Beispiel
1. "Hoch 1"-Regel	$$\log_a a=1$$	weil $a^1=a$. Z.B.: $$\ln e=1$$ oder $$\lg 10=1$$
2. "Hoch 0"-Regel	$$\log_a 1=0$$	weil $a^0=1$ für alle $a\neq 0$. Z.B.: $$\ln 1=0$$
3. Produktregel	$$\log_a (u\cdot v)=\log_a u+\log_a v$$	$a^x\cdot a^y=a^{x+y}$ und $u=a^x$ bzw. $v=a^y$
4. Quotientenregel	$$\log_a \left(\frac{u}{v}\right)=\log_a u-\log_a v$$	$\frac{a^x}{a^y}=a^{x-y}$ und $u=a^x$ bzw. $v=a^y$
5. Exponentenregel	$$\log_a u^r = r\cdot \log_a u$$	$\left(a^x\right)^r=a^{r\cdot x}$
6. "Negativ-Regel"	$$\log_a (u\pm v)=log_a (u\pm v)$$	Bei einer Summe oder Differenz kann man nichts verändern!
7. Umrechnung im Taschenrechner	$$\log_a u =\frac{\log_b u}{\log_b a}$$	Mit dieser Formel lassen sich Logarithmen mit beliebiger Basis im TR berechnen. Z.B.: $$\log_2 1024 = \frac{\ln 1024 }{\ln 2}=10$$

Musterbeispiele

Merke

Hinweis Bei den folgenden Beispielen ist es egal, mit welcher Basis gerechnet wird, da die obigen Regeln für alle Basen $a>0$ gelten. Bei den folgenden Umformen gehen wir "von außen nach innen", d.h. wir formen zuerst jene Rechenoperationen um, die sich auf den ganzen Term im Logarithmus bezieht.

Forme durch Verwenden der Rechenregeln des Logarithmus auf:

$$\ln\left(a^3\cdot b\right)$$

$$\ln\left(a^3\cdot b\right)\underbrace{=}_{3.Regel} \ln(a^3)+ \ln(b)\underbrace{=}_{5.Regel} 3\cdot \ln(a)+\ln(b)$$

$$\lg\left(\frac{a^5\cdot \sqrt[3]{b} }{c^2} \right)$$

$\begin{align} \lg\left(\frac{a^5\cdot \sqrt[3]{b} }{c^2} \right)&\underbrace{=}_{4.}& \lg(a^5\cdot b^\frac{1}{3} )-\lg(c^2)\\ & \underbrace{=}_{3.}& \lg(a^5)+lg( b^\frac{1}{3} )-lg(c^2)\\ & \underbrace{=}_{5}& 5\cdot \lg(a)+\frac{1}{3}\cdot \lg(b)-2\cdot \lg(c) \end{align}$

$$\lg\sqrt[5]{\left(\frac{(a^2-b^2)\cdot c^3}{10^{-3}\cdot (a+b)} \right)}$$

$\begin{align} \lg\sqrt[5]{\left(\frac{(a^2-b^2)\cdot c^3}{10^{-3}\cdot (a+b)} \right) } &\underbrace{=}_{umformen}& \lg \left(\frac{(a-b)\cdot (a+b)\cdot c^3}{10^{-3}\cdot (a+b)} \right)^{\frac{1}{5} }\\ &\underbrace{=}_{5.+kürzen}& \frac{1}{5}\lg \left(\frac{(a-b)\cdot c^3}{10^{-3} } \right)\\ &\underbrace{=}_{4.}& \frac{1}{5}\left[ \lg\left((a-b)\cdot c^3\right)-\lg(10^{-3})\right]\\ &\underbrace{=}_{3.}&\frac{1}{5}\left[ \lg(a-b)+ \lg c^3-\lg(10^{-3})\right]\\ &\underbrace{=}_{ 5.}&\frac{1}{5}\left[ \lg(a-b)+ 3\cdot\lg c-(-3)\cdot\lg(10)\right]\\ &\underbrace{=}_{\lg(10)=1} & \frac{1}{5}\lg(a-b)+\frac{3}{5}\cdot \lg(c)+\frac{3}{5} \end{align}$

Gleichungen mithilfe des Logarithmus lösen

Für Anwendungsbeispiele ist vor allem die 5. Regel von Bedeutung, da sie es uns erlaubt, Gleichungen zu lösen, indenen die Variable im Exponenten steht.

$$5^x=13$$ Bestimme den Wert von x!

Allein durch einfaches abschätzen wissen wir schon, dass x zwischen 1 und 2 liegen muss (da $5^1=5$ und $5^2=25$). Den genauen Wert können wir aber erst mit dem Logarithmus bestimmen.

$$5^x=13 \ \ \vert \lg(\ )$$ $$\lg(5^x)=\lg(13)\ \ \vert 5.\ Regel$$ $$x\cdot \lg(5)=\lg(13)\ \ \vert :\lg(5)$$ $$x=\frac{\lg(13)}{\lg(5)}=1.59$$

Merke

* Wende den Logarithmus erst so spät wie möglich an! So gehst du den häufigsten Fehlern aus dem Weg! Es ist egal, ob du $\ln$ (Logarithmus zur Basis $e$) oder $\lg$ (Logarithmus zur Basis 10) verwendest. Wichtig ist nur, dass du in einer Rechnung die Basis nicht mischt. Rechentechnisch es es ratsam $\ln$ zu verwenden, wenn die $e$ als Basis vorkommt und $\lg$ zu verwenden, wenn 10 als Basis vorkommt. Die Begründung liegt in Regel 1: $\lg(10)=\ln(e)=1$

Bestimme x: $$2^{x+3}=16$$

$$2^{x+3}=16\ \ \ \ \vert \lg $$

$$(x+3)\cdot \lg 2= lg 16 \vert \ \ \ \ :\lg 2$$ $$ x+3=\frac{lg 16}{lg 2}\ \ \ \vert -3$$ $$x=\frac{lg 16}{lg 2}-3$$ $$x=1$$ Selbstverständlich hätte man auch schon zu Beginn sehen können, dass x=1 eine Lösung der Gleichung $2^{x+3}=16$, weil $2^4=16$ ist.

$$N_t=N_0\cdot e^{\lambda\cdot t}$$ Stelle $t$ frei!

$\begin{align} N_t=&N_0\cdot e^{\lambda\cdot t}& \vert :N_0\\ \frac{N_t}{N_0}=&e^{\lambda\cdot t}& \vert \ln(\ )\\ \ln\left(\frac{N_t}{N_0}\right)=&\ln\left(e^{\lambda\cdot t}\right)& \vert 5.\ Regel\\ \ln\left(\frac{N_t}{N_0}\right)=&(\lambda\cdot t)\cdot \ln(e)& \vert \ln(e)=1\\ \ln\left(\frac{N_t}{N_0}\right)=&\lambda\cdot t & \vert :\lambda \\ \frac{\ln\left(\frac{N_t}{N_0}\right) }{\lambda}=&t& \end{align}$

weitere Materialien

• Inforamtionen auf Brinkmann-du.de
• Übungen von Jutta Gut

Beispiele

kommt bald