Extremstellen

Extremstellen

Im Graphen sind die beiden Extremstellen $x_1$ und $x_2$ samt den dazugehörenden Hoch- und Tiefpunkten eingezeichnet.

Definition

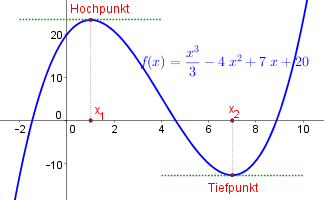
Lokale Extremstellen sind jene Stellen ($=x$-Werte), an denen der Graph der Funktion einen lokalen Hoch- oder Tiefpunkt hat. Formale Definition: Eine Funktion $f$ hat bei $x_0$ einen lokalen Hochpunkt, wenn für alle $x$ in einer Umgebung von $x_0$ gilt, dass $f(x)<f(x_0)$. (Analog funktioniert die Definition für einen lokalen Tiefpunkt.)

Video

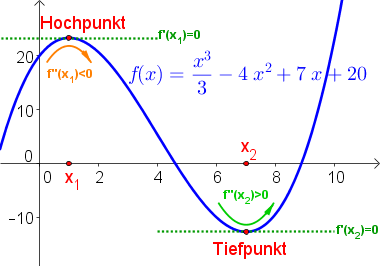
Wie am Graphen in der rechten Abbildung erkennbar ist, sind die Steigungen an den Extremstellen immer $0$ (d. h. beim Hochpunkt und Tiefpunkt steigt $f$ nicht und fällt $f$ nicht). Somit gilt $f'(x)=0$.

Zusätzlich ist der Graph beim Hochpunkt rechtsgekrümmt (d. h. $f''(x)<0$) und beim Tiefpunkt linksgekrümmt (d. h. $f''(x)>0$).

Somit erhalten wir...

Hinreichende Bedingung für ein lokales Extremum

Merke

$f'(x_0)=0$ und $f''(x_0)< 0$ $\Rightarrow\ \ \ \ $ $x_0$ ist die Stelle eines lokalen Hochpunktes (Maximums) von $f$ $f'(x_0)=0$ und $f''(x_0)>0$ $\Rightarrow\ \ \ \ $ $x_0$ ist die Stelle eines lokalen Tiefpunktes (Minimums) von $f$ $f'(x_0)=0$ und $f''(x_0)=0$ $\Rightarrow\ \ \ \ $ dann muss hier nicht unbedingt ein Extremum sein.

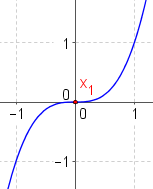
Der letzte Punkt ($f'(x_0)=0$ ABER $f''(x_0)=0$) wird klar, wenn man sich die Funktion $f(x)=x^3$ ansieht:

Beispiel für $f''(x)=0$, aber kein Extremum: $f(x)=x^3$

Graph von $f(x)=x^3$

Sei $f(x)=x^3$. Um die Extrema zu berechnen, setzen wir $f'(x)=0$ und bestimmen dann $f''(x)$ an dieser Stelle:

$f'(x)=3x^2$ $0=3x^2$ $\rightarrow x=0$

$\ $ und $\ \ \ \ $

$f''(x)=6x$ $f''(0)=0$

Somit ist $f'(0)=0$ und $f''(0)=0$. Wie man aber leicht am Graphen erkennt, ist bei $x_1=0$ kein Extremum (weder Hoch- noch Tiefpunkt).

Die Bedingungen $f''(x_0)<0$ (für ein Maximum) und $f''(x_0)>0$ (für ein Minimum) sind also wichtig.

Musterbeispiel

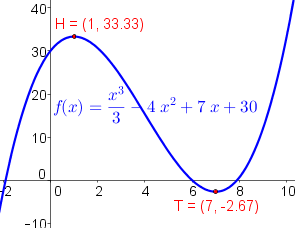
Bestimme die Extrema der Funktion $\ f(x)=\frac{x^3}{3}-4x^2+7x+30$.

Lösung:

Zuerst bestimmen wir die 1. Ableitung $f'(x)$ und die zweite Ableitung $f''(x)$: $$f(x)=\frac{x^3}{3}-4x^2+7x+30$$ $$f'(x)=x^2-8x+7$$ $$f''(x)=2x-8$$

Nun setzen wir die 1. Ableitung $0$ (da die Steigung bei Hoch- und Tiefpunkt $0$ ist): $$0=x^2-8x+7$$ $$x_{1,2}=\frac{8\pm \sqrt{64-4\cdot 7} }{2}$$ $$x_{1,2}=\frac{8\pm 6}{2}$$ $$x_1=1$$ $$x_2=7$$

Graph mit Hoch- und Tiefpunkt

Somit haben wir $2$ mögliche Extremstellen gefunden. Nun müssen wir noch überprüfen, ob es sich um Hoch- oder Tiefpunkte (oder weder noch) handelt. Hierzu setzen wir $x_1=1$ und $x_2=7$ in die zweite Ableitung ein:

$f''(1)=2\cdot 1-8=-6<0 \rightarrow $ rechtsgekrümmt $\rightarrow$ Hochpunkt

$f''(7)=2\cdot 7-8=+6>0 \rightarrow $ linksgekrümmt $\rightarrow$ Tiefpunkt

Somit wissen wir, dass sich bei $x=1$ ein Hochpunkt und bei $x=7$ ein Tiefpunkt befindet. Zuletzt bestimmen wir nun noch die $y$-Koordinaten des Hoch- und Tiefpunktes. Hierzu setzen wir die $x$-Werte in die ursprüngliche Funktion $f(x)$ ein:

$f(1)=\frac{1^3}{3}-4\cdot 1^2+7\cdot 1+30=33.33\rightarrow H(1\vert 33.33)$

$f(7)=\frac{7^3}{3}-4\cdot 7^2+7\cdot 7+30=-2.67\rightarrow T(7\vert -2.67)$