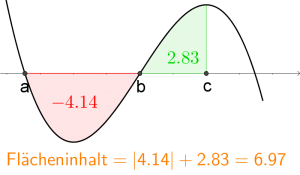Integration

Integration

• Unbestimmtes Integral
• Idee der Integration
• Bestimmtes Integral
• Anwendung 1
• Anwendung 2
• Anwendung 3
• Technologieeinsatz
• Übungs- und Maturaaufgaben

Berechnung der Stammfunktion

Für fast jede uns bekannte Rechenoperation existiert auch eine Umkehroperation (siehe Äquivalenzumformungen). Die Umkehroperation der Addition ist zum Beispiel die Subtraktion.

Die passende Umkehroperation zum Differenzieren (Ableitungen bestimmen) ist die Integration.

Wir haben bereits gelernt, dass wir zu einer Funktion $f$ die Ableitungsfunktion $f'$ bestimmen können mithilfe der Ableitungsregeln. Nun sollte es natürlich möglich sein, zu einer Ableitungsfunktion die dazugehörige Ausgangsfunktion zu finden. Man kann jede Funktion als Ableitung betrachten und demnach muss es zu jeder Funktion (die man selbst ableiten kann) auch eine Funktion geben, aus der sie durch Ableiten hervorgegangen ist. Diese Überlegung führt uns zum Begriff Stammfunktion.

Definition

Stammfunktion Die Funktion $F$ heißt Stammfunktion der Funktion $f$, wenn gilt: $$F'(x)=f(x)$$ Eine andere Schreibweise, die wir erst später rechtfertigen, ist: $$F(x)=\int f(x)\cdot dx$$

Musterbeispiel

$f(x)=2x$

$\rightarrow$

$F_1(x)=x^2$ $F_2(x)=x^2+3$ $F_3(x)=x^2-7.2$

weil $F_1'(x)=2x$ weil $F_2'(x)=2x$ weil $F_3'(x)=2x$

Alle diese Funktionen $F_1,\ F_2$ und $F_3$ sind Stammfunktionen von $f(x)=2x$, da die konstanten Zahlen durch das Ableiten wegfallen. Aus diesem Grund geben wir eine allgemeine Stammfunktion an:

Allgemeine Stammfunktion

$f(x)=2x \ \ \ \rightarrow \ \ \ F(x)=x^2+c$ mit $c\in$ $\mathbb{R}$.

weil $F'(x)=f(x) \leftrightarrow (x^2+c)'=2x$

Merke

Integrationskonstante $c$ Die Integrationskonstante $c$ ist jener unbekannte konstante Term ($c\in$ $\mathbb{R}$) der Stammfunktion, der durch das Ableiten wieder wegfällt. Wir sehen also, dass die Integration keine exakte Umkehrung des Differenzierens ist, da wir die Integrationskonstante $c$ ohne weitere Informationen nicht wieder zurückgewinnen können.

Beispiele

$f(x)=5$

$F(x)=5x+c$ weil $F'(x)=5$

$f(x)=3x^2$

$F(x)=x^3+c$ weil $F'(x)=3x^2$

$f(x)=x^2$

$F(x)=\frac{x^3}{3}+c$ weil $F'(x)=\frac{3\cdot x^2}{3}=x^2$

$f(x)=5x+2$

$F(x)=\frac{5x^2}{2}+2x+c$ weil $F'(x)=5x+2$

Integrationsregeln

	Regel	Bemerkung
Potenzregel	$$\int x^n\,dx=\frac{x^{n+1}}{n+1}+c$$	Exponent um $1$ erhöhen und mit dem neuen Exponenten dividieren. Die Potenzregel gilt für alle Potenzen mit $n\neq -1$
Summenregel	$$\int [f(x)± g(x)]\,dx=\int f (x)\,dx±\int g (x)\,dx$$	Eine Summe wird integriert, indem man jeden Summanden einzeln integriert.
Faktorregel	$$\int c\cdot f (x)\,dx=c\cdot\int f (x)\,dx$$	Einen konstanten Faktor kann man herausheben. Dies gilt auch für Brüche.
Regel für $\frac{1}{x}$	$$\int \frac{1}{x}\,dx=In|x|+c$$	Wobei $ln(x)$ der Logarithmus zur Basis $e$ ist. Diese Regel braucht man für $\frac{1}{x}=x^{-1}$
Regel für die Exponentialfunktion $e^x$	$$\int e^x=e^x+c$$	Wie beim Ableiten ändert sich auch beim Integrieren nichts.
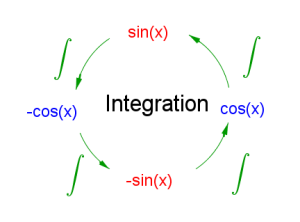
Trigonometrische Funktionen	$$\int sin(x)\cdot dx=-cos(x)+c$$ $$\int cos(x)\cdot dx=sin(x)+c$$	Integrationsregeln für die Sinus- und Cosinusfunktion

Beispiele

Bestimmen Sie alle Stammfunktionen:

$f(x)=3.7$

$F(x)=\int 3.7\cdot dx=3.7x+c$

$f(x)=2x+3$

$\int (2x+3)\cdot dx=x^2+3x+c$

$f(x)=-x+\frac{1}{2}$

$\int\left(-x+\frac{1}{2}\right)\cdot dx=-\frac{x^2}{2}+\frac{1}{2}x+c\ \ \ \ \ \ \ \ (\textrm{oder: }-0.5x^2+0.5x+c)$

$f(x)=\frac{x^2}{2}$

$\int \left( \frac{x^2}{2}\right) \cdot dx=\frac{x^3}{3\cdot 2}+c=\frac{x^3}{6}+c$

$f(x)=9x^2-8x+7$

$\int (9x^2-8x+7)\cdot dx=3x^3-4x^2+7x+c$

$f(x)=\frac{1}{x}$

$\int \frac{1}{x}\cdot dx=In\vert x\vert +c$

$f(x)=\frac{1}{x^2}+x^{-3}-\frac{5}{3}$

$\int x^{-2}+x^{-3}-\frac{5}{3}\cdot dx=\frac{x^{-1} }{-1}+\frac{x^{-2} }{-2}-\frac{5}{3}\cdot x +c=-\frac{1}{x}-\frac{1}{2x^2}+\frac{5}{3}\cdot x+c$

Interaktive Übungen

Quiz: Ableitungsfunktion/Stammfunktion (AN 3.1)

Zusatzmaterial

Die folgenden Materialien wurden von Schüler*innen der HLW Marienberg erstellt:

? $\ $ Kreuzworträtsel zum unbestimmten Integral

? $\ $ Zuordnungsaufgaben zu den Integrationsregeln

$\rightarrow$ nächste Seite ...

Fläche als Summe unendlich kleiner Rechtecke

Ober- und Untersummen

Abbildungen der a) Untersumme und b) Obersumme bei 6 Rechtecken

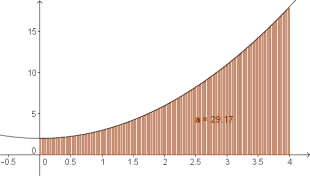
In diesem Kapitel wollen wir die tatsächliche Fläche unter einer Kurve annähernd berechnen (siehe Abbildung oben). Dies machen wir auf zwei Arten:

a) Wir zeichnen viele Rechtecke unter die Kurve (siehe Abbildung) und addieren dann Rechtecksflächen (= Untersumme). Damit erhalten wir eine Fläche die sicherlich kleiner als die tatsächliche Fläche unter der Kurve ist.

b) Nun zeichnen wir viele Rechtecke über die Kurve und addieren dann wieder die Rechtecksflächen (= Obersumme). Das Ergebnis muss größer sein, als der tatsächliche Inhalt unter der Kurve.

Wie können wir damit aber den tatsächlichen Flächeninhalt unter der Kurve berechnen?

Merke

Die Idee ist nun, beliebig viele Rechtecke einzuschreiben. $Aha!$ $\ $ Wie du an diesem Applet erkennen kannst, nähern sich die Ober- und Untersumme immer mehr dem tatsächlichen Flächeninhalt an.

Wie ist dieses Applet zu bedienen?

1. Klicke links unten auf das „Play“-Symbol oder verschiebe den Schieberegler „Rechtecksanzahl“.
2. Beobachte, wie sich die Untersumme immer mehr der tatsächlichen Fläche annähert.
3. Klicke dann auf das Kästchen „Obersumme“ und wiederhole hier die Schritte 1 und 2.

Die orientierte Fläche unter einer Kurve kann somit als Grenzwert (= Limes) der Summe von unendlich vielen Rechtecken mit der Höhe $f(x)$ und einer unendlich kleinen Breite berechnet werden.

Formale Berechnung und Schreibweise

Die Berechnung der Ober- und Untersumme funktioniert nun folgendermaßen:

Die Fläche eines einzelnen Rechteckes ist $f(x_1)\cdot \Delta x$.

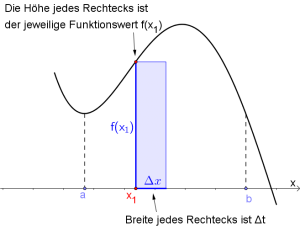
1. Zuerst berechnen wir die Fläche eines der Rechtecke. Dieses hat die Breite $\Delta x$ und die Höhe $f(x_1)$ (da die Höhe an der Stelle $x_1$ ja dem Funktionswert von $f$ entspricht). Somit gilt: $$Inhalt\ eines\ Rechtecks=f(x_1)\cdot \Delta x$$
2. Dann summieren wir über alle Rechtecke, um die Unter- bzw. Obersumme zu erhalten: $$\sum_{i=1}^{n} f(x_i)\cdot \Delta x$$
3. Im letzten Schritt bilden wir unendlich viele Summen, da wir aus dem vorigen Applet wissen, dass wir damit der tatsächlichen Fläche beliebig nahe kommen:

$$\lim_{n\rightarrow \infty}\sum_{i=1}^{n}\underbrace{f(x_i)\cdot \Delta x}_{\textrm{Fläche eines Rechteckes}}=\int_{a}^{b} f(x)\cdot dx$$ Der letzte Term $\int_{a}^{b} f(x)\cdot dx$ ist nun die verkürzte Schreibweise für „die unendliche Summe aller Rechtecksinhalte zwischen $a$ und $b$“. Der Term $\int_{a}^{b} f(x)\cdot dx$ wird so ausgesprochen: „das Integral zwischen $a$ bis $b$ von $f(x)$ mal $dx$“

Bedeutung der einzelnen Terme: $$\lim_{n\rightarrow \infty}\sum_{i=1}^{n} f(x_i)\cdot \Delta x=\int_{a}^{b} f(x)\cdot dx$$

• $f(x_i)$...Höhe eines Rechtecks
• $\Delta x$ .... Breite eines Rechtecks
• $f(x_i)\cdot \Delta x$...Fläche eines Rechtecks
• $\sum_{i=1}^{n}$... Summe aller n Rechtecksflächen
• $\int $ unendliche Summe (= Integrationszeichen) und damit eine verkürzte Schreibweise für $\lim_{n\rightarrow \infty}\sum_{i=1}^{n}$
• $dx$...unendlich kleine Breite eines Rechtecks
• $\int_{a}^{b} f(x)\cdot dx$... unendliche Summe aller Rechtecksflächen zwischen $a$ und $b$

$$\int_{a}^{b} f(x)\cdot dx$$

• $f(x)$ heißt Integrand (das, was integriert wird)
• $x$ heißt Integrationsvariable
• $a$ und $b$ heißen untere bzw. obere Integrationsgrenze
• $\int_{a}^{b} f(x)\cdot dx$ ist das bestimmte Integral und gibt die orientierte Fläche zwischen $f(x)$ und der $x$-Achse an.

Merke

$\int f(x) \cdot dx$ bezeichnet das unbestimmte Integral, es hat keine Grenzen und berechnet die Stammfunktionen von $f$. $\int_{a}^{b} f(x)\cdot dx$ bezeichnet das bestimmte Integral zwischen $a$ und $b$ und berechnet die orientierte Fläche. Über das bestimmte Integral wirst du im nächsten Kapitel noch mehr lernen.

Beispiel

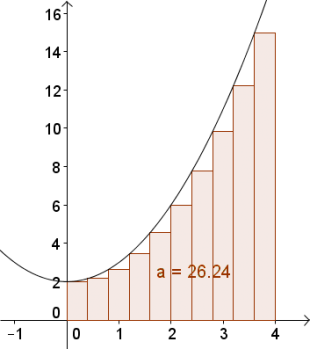
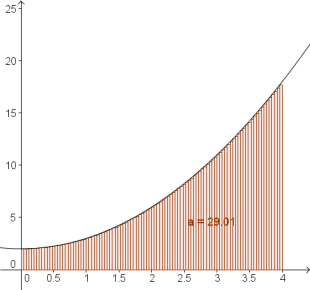
Im folgenden Beispiel ist die Funtkion $f(x)=x^2+2$ gegeben und es wird die Fläche zwischen $0$ und $4$ mithilfe von Rechtecken berechnet. Die tatsächliche Fläche beträgt $a=29.33$ FE.

• Je größer die Anzahl der Rechtecke, desto näher liegt die Untersumme am tatsächlichen Flächeninhalt.
• 

  10 Rechtecke

• 

  100 Rechtecke

• 

  200 Rechtecke

$\rightarrow$ nächste Seite ...

Berechnung der orientierten Fläche

Merke

Was wir bereits wissen: Das unbestimmte Integral $\int f(x)\cdot dx$ berechnet die Stammfunktion $F(x)$ (siehe unbestimmtes Integral ). Das bestimmte Integral bereichnet $\int_{a}^{b} f(x)\cdot dx$ bestimmt die orientierte Fläche zwischen der Kurve von $f(x)$ und der $x$-Achse in den Grenzen zwischen $a$ und $b$ (siehe Idee der Integration ). Was wir allerdings noch nicht wissen: Wie rechnen wir den Flächeninhalt nun konkret aus? Wie hängt das bestimmte Integral und das unbestimmte Integral zusammen?

Die Antwort auf beide dieser Fragen liefert ...

Der Hauptsatz der Integration

Definition

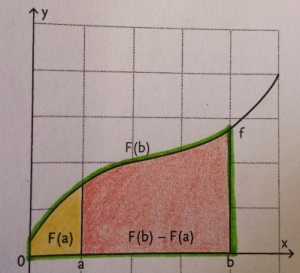
Für eine stetige Funktion $f$ gilt: Ist $F$ eine (beliebige) Stammfunktion von $f$, das heißt $F' = f$, dann gilt: $$ \int_{a}^{b} f (x)\,dx = F(x)\vert _{a}^{b} = F(b) - F(a) $$ D. h.: Die orientierte Fläche zwischen $a$ und $b$ wird berechnet, indem zuerst die Stammfunktion bestimmt wird, dann setzt man die Grenzen ein und subtrahiert nach dem Prinzip „Obere Grenze MINUS Untere Grenze“.

- $F(a)$ = gelbe Fläche
- $F(b)$ = grün-umrandete Fläche
- $F(b)-F(a)$ = rote Fläche $= \int_{a}^{b} f (x)\cdot dx $

Wiederholung der Bezeichnungen

• $f(x)$ heißt Integrand ( das, was integriert wird)
• $x$ ist die Integrationsvariable
• $a$ und $b$ sind die untere bzw. obere Integrationsgrenze
• $\int_{a}^{b} f (x)\,dx$ ist das bestimmte Integral und gibt die orientierte Fläche zwischen $f(x)$ und der $x$-Achse an

Bemerkungen:

1. $F(b)$ berechnet die orientierte Fläche zwischen $0$ und der Grenze $b$. $F(a)$ berechnet die orientierte Fläche zwischen $0$ und $a$. Somit kann die Fläche zwischen $a$ und $b$ mithilfe von $F(b)-F(a)$ bestimmt werden. So kommt man auf die Formel des 2. Hauptsatzes.
2. Wichtig ist, dass man immer zuerst die obere Grenze einsetzt und dann erst die untere Grenze. Ansonsten hat das Ergebnis das falsche Vorzeichen. $$ \int_{\color{red}{untere\ Grenze} }^{\color{red}{obere\ Grenze} } \color{green}{f(x)} \cdot \color{blue}{dx}=F(\color{red}{obere\ Grenze} )-F(\color{red}{untere\ Grenze}) $$
3. $\int_{a}^{b} f (x)$ bezeichnet die orientierte Fläche. Ist die Fläche unterhalb der $x$-Achse, so hat sie ein negatives Vorzeichen.

Dieses Video fasst noch einmal die wichtigsten Punkte zusammen (WICHTIG: bitte nur bis zur Minute 2:30 ansehen ):

Musterbeispiele

Merke

Schrittfolge zur Berechnung des bestimmten Integrals: Schritt: Ermittele die Stammfunktion $F$. Schritt: Ermittele $F(b)$ und $F(a)$ (Die Grenzen $a$ und $b$ in $F$ einsetzen). Schritt: Berechne die Differenz $F(b)-F(a)$.

$\int_{1}^{2} (6x^2 + x-2)\,dx = $

$$\int_{1}^{2} (6x^2 + x-2)\,dx =\underbrace{2x^3+\frac{x^2}{2}-2x+c\vert _{1}^{2} }_{1.\ Schritt} = \underbrace{\left[2\cdot 2^3+\frac{2^2}{2}-2\cdot 2+c\right]-\left[2\cdot 1^3+\frac{1^2}{2}-2\cdot 1+c\right]}_{2.\ Schritt}=\underbrace{(14+c) - (0.5+c) = 13.5}_{3.\ Schritt}$$

Merke

Die Integrationskante $c$ fällt bei bestimmten Integralen immer weg. Daher schreiben wir sie in Zukunft beim bestimmten Integral nicht mehr an.

$\int_{1}^{3} \left(\frac{1}{x}-\frac{2}{x^2}+\frac{3}{x^3}\right)\, dx =$

$$\int_{1}^{3} \left(\frac{1}{x}-\frac{2}{x^2}+\frac{3}{x^3}\right)\,dx = \underbrace{In\vert x\vert +\frac{2}{x}-\frac{3}{2x^2}\vert _{1}^{3} }_{1.\ Schritt}=\underbrace{ \left[In (3) + \frac{2}{3}-\frac{1}{6}\right]-\left[In (1)+2-\frac{3}{2}\right]}_{2.\ Schritt} = \underbrace{In 3 \approx 1.0986}_{3.\ Schritt}$$

Weitere Beispiele

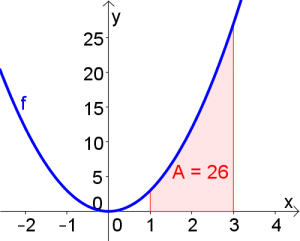
Bestimmen Sie die Werte der folgenden bestimmten Integrale. Fertigen Se eine Skizze an, in der die berechnete Fläche eingezeichnet ist.

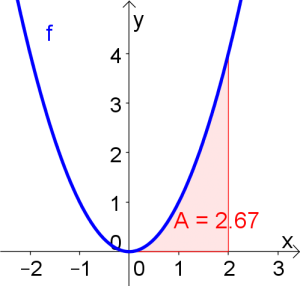
$\int\limits_{0}^{2}x^2dx$

$$\int\limits_{0}^{2}x^2dx= \frac{x^3}{3}\vert_{0}^{2} = \frac{2^3}{3}- \frac{0^3}{3} = \frac{8}{3} \approx 2.67$$

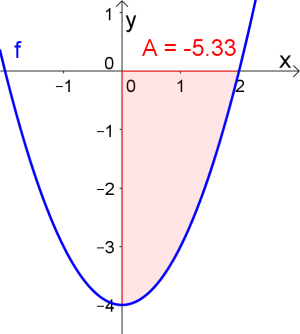
$\int\limits_{0}^{2}\left( x^2-4\right)\ dx$

$$\int\limits_{0}^{2}\left( x^2-4\right)\ dx= \frac{x^3}{3}-4x\vert_{0}^{2} =\left[\frac{2^3}{3}-4\cdot 2\right]- \left[\frac{0^3}{3}-4\cdot 0\right] = \frac{8}{3}-8 = -\frac{16}{3}\approx -5.33$$ ACHTUNG: Du erhältst ein negatives Ergebnis, weil die Fläche unterhalb der $x$-Achse ist (siehe orientierte Fläche).

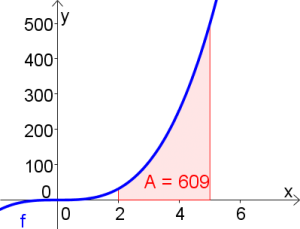
$\int\limits_{1}^{3} 3x^2dx$

$$\int\limits_{1}^{3} 3x^2dx= 3\frac{x^3}{3}\vert_{1}^{3} = 3\frac{3^3}{3}- 3\frac{1^3}{3} = 27-1 = 26$$

$\int\limits_{2}^{5} 4x^3dx$

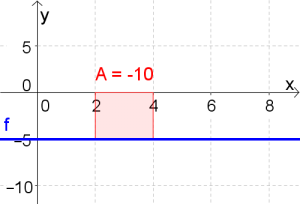
$$\int\limits_{2}^{5} 4x^3dx= 4\frac{x^4}{4}\vert_{2}^{5} = 4\frac{5^4}{4}- 4\frac{2^4}{4} = 625-16 = 609$$

$\int\limits_{2}^{4}-5dx$

$$\int\limits_{2}^{4}-5dx= -5\frac{x^1}{1}\vert_{2}^{4}=-5 \frac{4}{1}-\left(-5\frac{2}{1}\right) = -5\cdot 4 - \left(-5\cdot 2\right) = -20-(-10)=-10$$

Merke

Das bestimmte Integral gibt immer die orientierte Fläche zwischen dem Graphen und der $x$-Achse an.

Mit dieser Überlegung können auch kompliziertere Flächen berechnet werden:

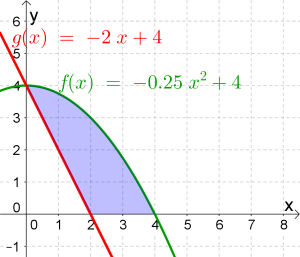
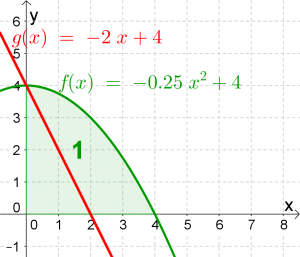
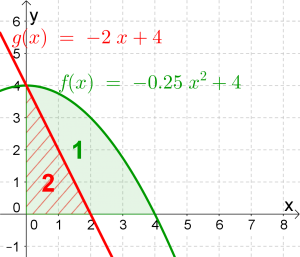
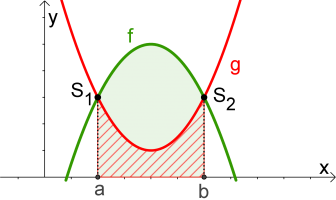
Bestimme den Inhalt der blau eingefärbten Fläche.

Da die blaue Fläche keine Fläche zwischen einem Graphen und der $x$-Achse ist, können wir sie nicht direkt berechnen. Allerdings hilft uns folgende Überlegung etwas:

• 

  Zieht man von der grünen Fläche (1) ...

• 

  .... die rote Fläche (2) ab, ...

• 

  ... so erhält man die blaue Fläche.

Damit ergibt sich die Formel: $$blaue\ Fläche=\underbrace{\int_0^4 f(x)dx}_{grüne\ Fläche}-\underbrace{\int_0^2 g(x)dx}_{rote\ Fläche}$$ $$blaue\ Fläche= \int_0^4 \left( -0.25x^2+4\right)dx-\int_0^2 \left( -2x+4\right) dx$$ Durch händische Berechnung oder mithilfe von Technologieeinsatz erhalten wir: $$blaue\ Fläche=\underbrace{10.\dot 6}_{grüne\ Fläche}-\underbrace{4}_{rote\ Fläche}=\underline{\underline{6.\dot 6} }$$

Hinweis: Selbstverständlich hätten wir die rote Fläche auch einfacher mithilfe der Flächenformel für rechtwinklige Dreiecke berechnen können.

Zusatzmaterialien

? $\ $ Übungsaufgaben zum bestimmen Integral (von Jutta Gut)

? $\ $ Übungen zum Lernen der Begriffe:

• Kreuzworträtsel
• Memory
• Hang Man

$\rightarrow$ nächste Seite ...

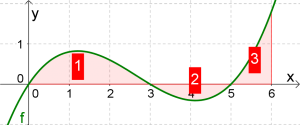
Berechnung von Flächen, die oberhalb und unterhalb der $x$-Achse liegen

Wir haben im vorigen Kapitel gelernt, einfache Flächen zu berechnen. Nun überlegen wir uns, wir wir kompliziertere Flächen berechnen können, die zum Teil oberhalb und zum Teil unterhalb der $x$-Achse liegen.

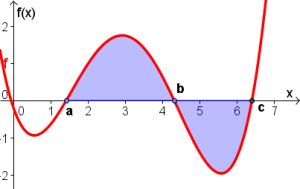
Wie können wir den in der Graphik eingezeichneten Flächeninhalt ausrechnen?

Zusätzliche Angabe: $f(x)=-0.13 x³ + 1.34x² - 3x, \textrm{ sowie } a=0,\ b=3.29 \textrm{ und } c=5.29$

Achtung: $\int_a^c f(x)dx=\int_0^{5.29} f(x)dx$ ist falsch!

Begründung:
Angenommen, wir würden simpel von $a=0$ bis $b=5.29$ rechnen, so erhielten wir nach dem Hauptsatz der Integration:

$$ \int_a^c f(x)dx=\int_0^{5.29} \left(-0.13 x³ + 1.34x² - 3x\right)\cdot dx=\left[-0.13\frac{x^4}{4}+1.34\frac{x^3}{3}-3\frac{x^2}{2}\right]_0^{5.29}=$$ $$=-0.13\frac{5.29^4}{4}+1.34\frac{5.29^3}{3}-3\frac{5.29^2}{2}=-1.3$$

Das Ergebnis $-1.3$ FE (FlächenEinheiten) kann aber aus zweierlei Gründen nicht der gesuchte Flächeninhalt sein:

1. Flächeninhalte sind immer positiv.
2. Würden wir in der obigen Abbildung den Flächeninhalt durch zählen der Kästchen abschätzen (jedes Kästchen hat eine Größe von $1x1$), so kämen wir ungefähr $6$ bis $7$ FE.

Wir können diese Fläche nicht einfach durch Integrieren von $a$ bis $c$ berechnen. Aus diesem Grund überlegen wir uns folgendes:

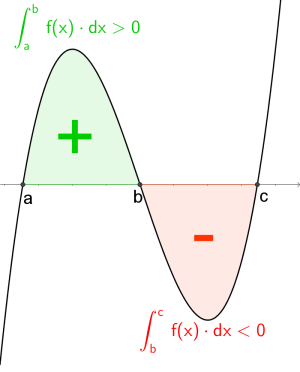
Idee

Flächen oberhalb der $x$-Achse sind positiv, Flächen unterhalb der $x$-Achse sind negativ.

Definition

Orientierte Fläche bedeutet: Liegt die Fläche oberhalb der $x$-Achse, so ist das bestimmte Integral positiv. Liegt die Fläche unterhalb der $x$-Achse so ist das bestimmet Integral negativ. Um den tatsächliche Flächeninhalt zu berechnen, müssen positive und negative Flächen getrennt voneinander berechnet werden.

Merke

Vorgehensweise zur Berechnung einer Fläche, die oberhalb und unterhalb der $x$-Achse liegt: Skizze erstellen, um zu überprüfen, ob Fläche oberhalb und unterhalb der $x$-Achse liegt. Grenzen und Nullstellen bestimmen (um zwischen positiver und negativer Fläche unterscheiden zu können) die positive Fläche berechnen (mithilfe des Hauptsatzes der Integration) die negative Fläche berechnen positive Fläche und den Betrag der negativen Fläche addieren.

Berechnung der Fläche unterhalb der x-Achse durch Betragstriche oder mithilfe eines negativen Vorzeichens.

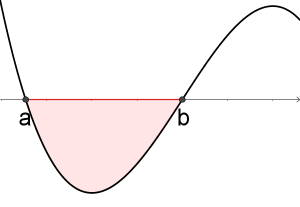
Bemerkungen:

• Bei negativen Flächen verwenden wir Betragsstriche um den Flächeninhalt positiv zu machen. Z. B.:

$$Flächeninhalt= \vert \int_a^b f(x)\cdot dx\vert $$

Alternativ kann statt der Betragsstriche auch ein Minus-Vorzeichen verwendet werden. Z. B.:

$$Flächeninhalt= -\int_a^b f(x)\cdot dx $$

• Aus diesen Überlegungen ergibt sich folgende Formel, um den Flächeninhalt im rechten Bild zu berechnen:

$$ \int_{a}^{b} f (x) + \vert \int_{b}^{c} f (x)dx \vert $$

oder

$$ \int_{a}^{b} f (x)dx - \int_{b}^{c} f (x)dx $$

Musterbeispiel

Berechne den Flächeninhalt der angegebenen Fläche wobei $f(x)=-0.13 x³ + 1.34x² - 3x, \textrm{ sowie } a=0, \ b=3.29 \textrm{ und } c=5.29$

Da die Skizze und die Nullstellen bereits bekannt sind, überspringen wir den 1. und 2. Schritt und starten beim

3. Schritt: Positive Fläche bestimmen

Die positive Fläche befindet sich zwischen $b=3.29$ und $c=5.29$. Somit erhalten wir: $$\int_{3.29}^{5.29}f(x)dx=\int_{3.29}^{5.29}\left(-0.13 x³ + 1.34x² - 3x\right) dx=\left[-0.13\frac{x^4}{4}+1.34\frac{x^3}{3}-3\frac{x^2}{2}\right]_{3.29}^{5.29}=$$ $$=\left[-0.13\frac{5.29^4}{4}+1.34\frac{5.29^3}{3}-3\frac{5.29^2}{2}\right] -\left[0.13\frac{3.29^4}{4}+1.34\frac{3.29^3}{3}-3\frac{3.29^2}{2}\right]=2.83$$

Den tatsächlichen Flächeninhalt erhältst du durch Addition der positiven Werte der einzelnen Flächen.

4. Schritt: Negative Fläche bestimmen $$\int_0^{3.29}f(x)dx=\int_0^{3.29}\left(-0.13 x³ + 1.34x² - 3x\right) dx=\left[-0.13\frac{x^4}{4}+1.34\frac{x^3}{3}-3\frac{x^2}{2}\right]_0^{3.29}=$$ $$=-0.13\frac{3.29^4}{4}+1.34\frac{3.29^3}{3}-3\frac{3.29^2}{2}-0=-4.14$$

5. Schritt: positive Fläche und den Betrag der negativen Fläche addieren

$$Flächeninhalt=\vert \int_0^{3.29} f(x)dx\vert + \int_{3.29} ^{5.29} f(x)dx=\vert -4.14\vert +2.83=6.97\ FE$$

Antwort: Der tatsächliche Flächeninhalt beträgt somit $6.97$ FE.

Weitere Beispiele

Die folgenden Beispiele wurden durch Einsatz von Technologie gelöst. Eine genaue Erklärung zur Verwendung von Technologie bei der Integration findest du im Kapitel Technologieeinsatz.

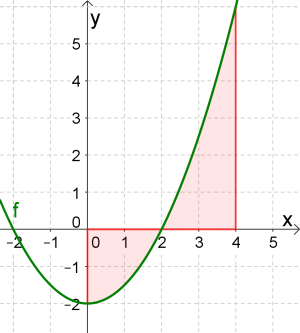
Berechne den Inhalt jener Fläche, der vom Graphen von $f$ mit $f(x)=\frac{x^2}{2}-2$ und der $x$-Achse im Intervall $[0;4]$ eingeschlossen wird.

1. Schritt: Skizze

Der gesuchte Flächeninhalt setzt sich aus einer linken, negativen Fläche und einer rechten, positiven Fläche zusammen.

2. Schritt: Grenzen und Nullstellen berechnen: $$f(x)=0$$ $$\frac{x^2}{2}-2=0$$ $$x^2=4$$ $$x_1=-2 \textrm{ und } x_2=2$$

Somit erhalten wir folgende Aufteilung der Flächen im Bereich $[0;4]$:

• negative Fläche von $0$ bis $2$
• positive Fläche von $2$ bis $4$

3. Schritt: Positive Fläche

$$\int_{2}^{4} f (x)dx=\frac{16}{3}$$

4. Schritt: Negative Fläche

$$\int_{0}^{2} f (x)dx=-\frac{8}{3}$$

5. Schritt: Addition der gesamten Fläche

$$\vert \int_{0}^{2} f (x)dx\vert + \int_{2}^{3} f (x)dx=$$ $$=\vert -\frac{8}{3} \vert + \frac{16}{3}=\frac{24}{3}=8$$

Antwort: Der gesuchte Flächeninhalt beträgt $8$ FE.

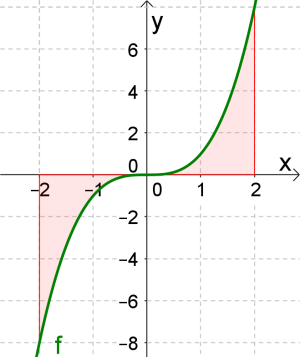
Gegeben ist die Funktion $f(x)=x^3$.


a) Begründe, warum $\int_{-2}^2 f(x)dx=0$ ist.
b) Berechne den Inhalt jener Fläche, der vom Graphen von $f$ und der $x$-Achse im Intervall $[-2;2]$ eingeschlossen wird.

a) Anhand der Skizze sieht man leicht, dass die Funktion punktsymmetrisch ist. Die Flächen links und rechts vom Ursprung heben sich auf.

Rechnerisch lässt sich dies leicht zeigen: $$\int_{-2}^2 x^3 dx= \left[ \frac{x^4}{4}\right]_{-2}^2=\frac{2^4}{4}-\frac{(-2)^4}{4}=\frac{16}{3}-\frac{16}{3}=0$$ Es gilt sogar allgemein für ein beliebiges Intervall $$\int_{-a}^a x^3 dx= \left[ \frac{a^4}{4}\right]_{-2}^2=\frac{a^4}{4}-\frac{(-a)^4}{4}=\frac{a^4}{3}-\frac{a^4}{3}=0$$

b) Nun wollen wir die Fläche berechnen. Hierzu gibt es $2$ Möglichkeiten.

1. Möglichkeit: Positive und negative Fläche addieren: Da wir, wie man anhand der Skizze erkennt, wieder eine negative und eine positive Fläche haben, rechnen wir beide einzeln und addieren anschließend die Beträge: $$\underbrace{\vert \int_{-2}^0 x^3 dx \vert}_{linke\ Fläche}+\underbrace{\int_{0}^2 x^3 dx}_{rechte\ Fläche}=$$ $$=\underbrace{\vert -4 \vert}_{linke\ Fläche}+\underbrace{4 }_{rechte Fläche}=\underline{\underline{8} }$$

2. Möglichkeit: Da die linke Fläche gleich groß ist wie die rechte Fläche, reicht es, nur eine von beiden zu berechnen und anschließend das Ergebnis zu verdoppeln: $$Fläche=2\cdot \int_{0}^2 x^3 dx=2\cdot 4=\underline{\underline{8} } $$

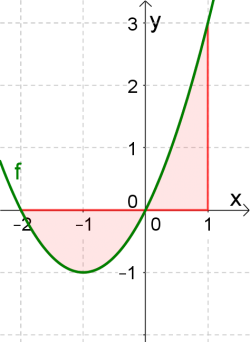
Berechne den Inhalt jener Fläche, der vom Graphen von $f$ mit $f(x)=x^2+2x$ und der $x$-Achse im Intervall $[-2;1]$ eingeschlossen wird.

1. Schritt: Skizze

2. Schritt: Grenzen und Nullstellen Die Nullstellen erhalten wir mit $f(x)=0$: $$x^2+2x=0$$ $$x\cdot (x+2)=0$$ $$\rightarrow x_1=0 \textrm{ und } x_2=-2$$

Der gesuchte Flächeninhalt teilt sich somit in eine linke, negative Fläche im Intervall $[-2;0]$ und eine rechte, positive Fläche im Intervall $[0;1]$ auf.

Schritte 3-5: $$\underbrace{\vert \int_{-2}^0 f(x) dx \vert}_{linke\ Fläche}+\underbrace{\int_{0}^1 f(x) dx}_{rechte\ Fläche}=\underbrace{\vert -\frac{4}{3} \vert}_{linke\ Fläche}+\underbrace{\frac{4}{3} }_{rechte Fläche}=\underline{\underline{\frac{8}{3}=2.\dot 6 } }$$

Berechne den Inhalt jener Fläche, der vom Graphen von $f$ mit $f(x)=0.1x^3 - 0.8x^2 + 1.5x $ und der $x$-Achse im Intervall $[0;6]$ eingeschlossen wird.

1. Schritt: Skizze

Die Fläche besteht aus insgesamt $3$ Teilflächen, die einzeln bestimmt werden müssen.

2. Schritt: Grenzen und Nullstellen Zuerst berechnen wir die Nullstellen: $$0.1x^3 - 0.8x^2 + 1.5x=0$$ $$x\cdot (0.1x^3-0.8x+15=0$$ $$\rightarrow x_1=0, x_2=3 \textrm{ und } x_3=5$$ Somit erhalten wir $3$ Teilflächen, die wir einzeln berechnen müssen:

1. Teilfläche: $[0;3]$, positiv
2. Teilfläche: $[3;5]$, negativ
3. Teilfläche: $[5;6]$, positiv

Schritte 3-5: $$\underbrace{ \int_0^3 f(x)dx}_{1}+\underbrace{\vert \int_3^5 f(x)dx\vert }_{2}+\underbrace{\int_5^6 f(x)dx}_{3}=$$ $$=\underbrace{ 1.58}_{1}+\underbrace{\vert -0.53\vert}_{2} +\underbrace{0.79}_{3}=\underline{\underline{2.9} }$$

Antwort: Der Inhalt der Fläche beträgt $2.9$ FE.

$\rightarrow$ nächste Seite ...

Berechnung von Flächen zwischen zwei Kurven

Das folgende Video bietet dir einen Überblick über das Gelernte und erklärt dir die Formel für die Fläche zwischen $2$ Kurven:

ab Minute 3:23 geht es um die Fläche zwischen 2 Kurven.

Flächeninhalt zwischen zwei Kurven

Definition

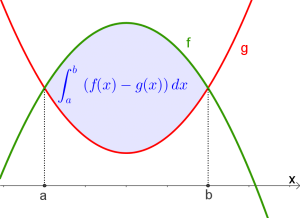
Formel zur Berechnung der Fläche zwischen $2$ Graphen Gegeben sei eine Fläche zwischen zwei Funktionsgraphen $f$ und $g$, dann kann der Inhalt der eingeschlossenen Formel mit dieser Formel berechnet werden: $$\int_a^b f(x)dx-\int_a^b g(x)dx \textrm{ bzw. } \int_a^b \left(f(x)-g(x)\right)dx$$ wobei der Graph von $f$ die obere und der Graph von $g$ die untere Begrenzungskurve sein muss! $$\int_{\color{blue}{linke\ Schnittstelle} }^{\color{blue}{rechte\ Schnittstelle} } \left(\color{green}{obere\ Funktion}-\color{red}{untere\ Funktion}\right)dx$$

$Aha!$ $\ $ Das folgende Applet zeigt dir die Herleitung dieser Formel

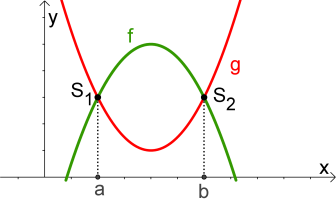
Herleitung der Formel als Bilderreihe

• 

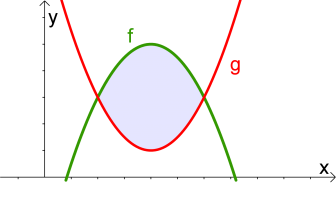
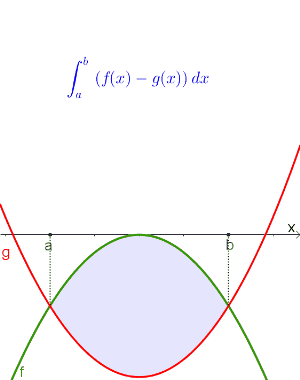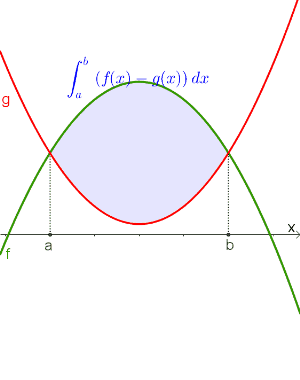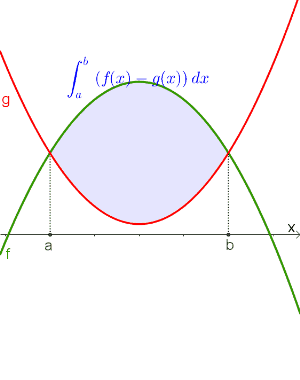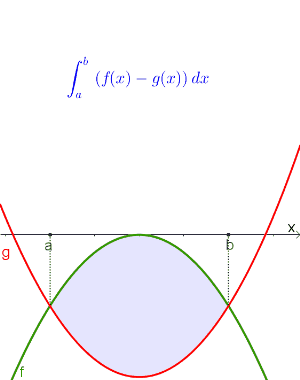
  Zuerst werden die Schnittpunkte bestimmt.

• 

  Als nächstes berechnet man die große Fläche mit $\int_a^b f(x) dx$ und ...

• 

  ... zieht davon die kleine Fläche $\int_a^b g(x)dx$ ab.

• 

  Als Ergebnis erhält man die gesuchte blaue Fläche.

Durch Verschieben beider Kurven entlang der $y$-Achse ändert sich der Flächeninhalt nicht. Somit ist die Formel auch gültig, wenn ein Teil der Fläche (oder die ganze) unter der $x$-Achse liegt.

Merke

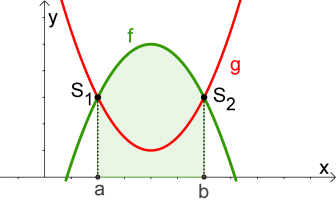
Rechne immer „obere Funktion“ MINUS „untere Funktion“. Ansonsten erhältst du ein negatives Ergebnis. Bei dieser Formel ist es egal, ob die Fläche oberhalb oder unterhalb der $x$-Achse ist. $$\int_a^b f(x)dx-\int_a^b g(x)dx$$ $Aha!$ $\ $ Dies kannst du im folgenden Applet überprüfen.

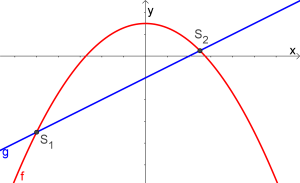
Exkurs: Wie werden Schnittpunkte berechnet und warum sind diese wichtig?

Die Koordinaten der Schnittpunkte $S_1$ und $S_2$ erhält man durch Lösen der Gleichung $f(x)=g(x)$.

Definition

Der Schnittpunkt zweier Funktionsgraphen ist jener Punkt, an dem beide Funktionen den gleichen $y$-Wert haben. Der Schnittpunkt kann berechnet werden, indem die Funktionen gleichsetzt: $$f(x)=g(x)$$ Die entstandene Gleichung wird nach $x$ aufgelöst. Man erhält den $x$-Wert des Schnittpunktes. Für den $y$-Wert des Schnittpunktes muss jetzt der $x$-Wert in eine der Funktionsgleichungen eingesetzt werden. (Es ist egal, in welche der beiden Funktionen, da der $y$-Wert bei beiden derselbe ist.) Der Schnittpunkt kann natürlich auch mithilfe von Technologie direkt berechnet werden: GeoGebra: Schneide-Werkzeug TI-Befehle: Intersect

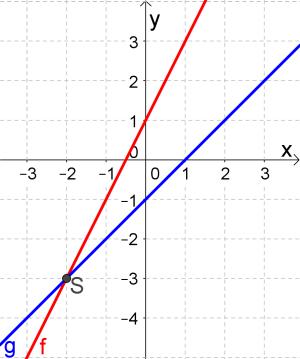
$f(x)=2x+1$ und $g(x)=x−1$. Ermitteln Sie den Schnittpunkt der beiden Funktionen.

300px Die Koordinaten des Schnittpunktes $S$ lauten $(-2\vert -3)$.

1. Schritt: Funktionen gleichsetzen. $$f(x)=g(x)$$ $$2x+1=x−1$$

2. Schritt: Gleichung nach $x$ auflösen (siehe Äquivalenzumformungen):

$$2x+1=x−1$$ $$2x=x−2$$ $$x=−2$$

Die $x$-Koordinate des Schnittpunktes lautet $x=-2$.

3. Schritt: $y$-Koordinate durch Einsetzen der $x$-Koordinate berechnen:

$$f(-2)=2\cdot (-2)+1$$

$$y=-3$$

Schnittpunkt: $(-2\vert -3)$

Merke

Schnittpunkte sind wichtig, weil sie uns zeigen, in welchem Bereich wir integrieren müssen.

Beispiele

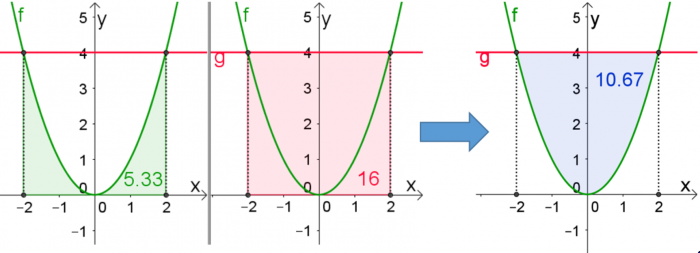
Berechnen Sie den Inhalt der Fläche, die von den Funktionen $f$ mit $f(x)=x^2$ und $g$ mit $g(x)=4$ umschlossen wird.

1. Schritt: Zuerst berechnen wir die Schnittpunkte:

$$f(x)=g(x)$$ $$x^2=4$$ $$x=\pm 2$$ Somit haben wir einen Schnittpunkt bei $x=-2$ und einen bei $x=2$ (Hinweis: Die $y$-Koordinaten sind für die weitere Berechnung nicht erforderlich.).

2. Schritt: Flächen berechnen und voneinander abziehen:

Indem man von der großen Fläche die kleine abzieht, erhält man die gesuchte Fläche.

Fläche unter $f(x)=A_{\cup}$
Fläche unter $g(x)=A_{ \Box }$
Dann ist die gesuchte Fläche $A$: $$A=A_{ \Box }-A_{\cup}$$

$A_{ \Box }=a\cdot a=4\cdot 4=16$
Alternativ kann man hier auch das bestimmte Integral verwenden: $$A_{ \Box }=\int_{-2}^2 g(x)dx=\int_{-2}^2 4dx=\left[ 4x\right]_{-2}^2=4\cdot 2-\left[ 4\cdot (-2)\right]=\underline{16}$$

$$A_{\cup}=\int_{-2}^2 f(x)dx=\int_{-2}^2 x^2dx=\left[\frac{x^3}{3}\right]_{-2}^2=\frac{2^3}{3}-\frac{(-2)^3}{3}=\frac{16}{3}\approx \underline{5.33}$$

Damit erhält man für $A$: $$A=A_{ \Box }-A_{\cup}=\int_{-2}^2 g(x)dx-\int_{-2}^2 f(x)dx$$ $$A=16-5.33=\underline{\underline{10.67} }$$ Wichtig: Da hier der Graph von $g$ oberhalb von $f$ liegt, muss man die Formel wie hier gezeigt anschreiben.

In den folgenden Beispielen wenden wir nun direkt die Formel an, ohne die Einzelheiten zu erklären:

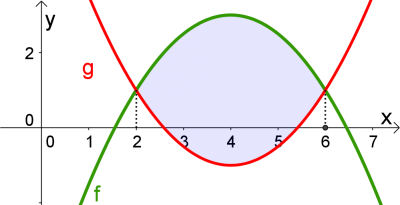
Berechne den Inhalt der Fläche, die von den beiden Funktionsgraphen $f$ mit $f(x)=-0.5 x² + 4x - 5$ und $g$ mit $g(x)=0.5x² - 4x + 7$ eingeschlossen wird. Fertige zuerst eine Skizze an.

1. Schritt: Schnittpunkte $$f(x)=g(x)$$ $$-0.5 x² + 4x - 5=0.5x² - 4x + 7$$ $$0=x^2-8x+12$$ $$x_1=2\textrm{ und } x_2=6$$

2. Schritt: Anwenden der Formel $$\int_a^b \left(f(x)-g(x)\right)dx$$ $$\int_2^6 \left((-0.5 x² + 4x - 5)-(0.5x² - 4x + 7))\right)dx$$ $$\int_2^6 \left(-x^2+8x-12\right)dx=10.67$$

Der gesuchte Flächeninhalt beträgt $10.67$ FE.

Merke

Wichtig ist immer, dass in der Formel immer die obere Funktion minus die untere Funktion berechnet wird. Besteht eine Fläche aus mehreren Teilschnittflächen, so muss in der Regel jede einzeln berechnet werden.

Dies muss in Beispielen wie dem Folgenden berücksichtigt werden:

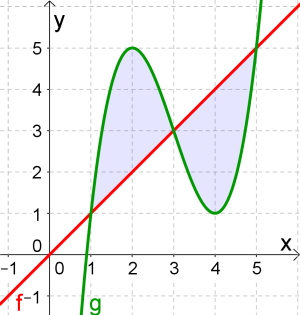
Berechne den Inhalt der blau eingefärbten Fläche, wobei $f(x)=x$ und $g(x)=x^3-9x^2+24x-15$ ist.

Berechne den Inhalt der blau eingefärbten Fläche

1. Schritt: Schnittpunkte

$$f(x)=g(x)$$ $$x=x^3-9x^2+24x-15$$ Mithilfe von Technologie erhält man: $$x_1=1,\ x_2=3 \textrm{ und } x_3=5$$

Jede der Teilflächen hat einen Inhalt von $4$ FE.

2. Schritt: Berechnung des Flächeninhaltes

Die gesuchte Fläche besteht aus zwei Flächeninhalten, die wir getrennt voneinander berechnen würden, weil $f$ und $g$ abwechselnd oben bzw. unten sind.

Die Rechnung $\int_1^5 (f(x)-g(x))dx$ wäre falsch, da hier $0$ herauskommt (prüfe es selbst nach).

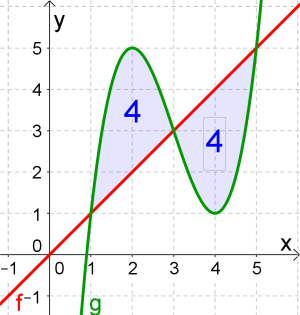
• Linke Fläche: Hier ist $g$ oben und $f$ unten:

$$\int_1^3 (g(x)-f(x))dx=\int_1^3 (x^3-9x^2+24x-15-x)dx=\underline{4}$$

• Rechte Fläche: Hier ist $f$ oben und $g$ unten:

$$\int_3^5 (f(x)-g(x))dx=\int_1^3 (x-(x^3-9x^2+24x-15))dx=\underline{4}$$

• Gesamt: $4+4=\underline{\underline{8} } $

Die eingeschlossene Fläche hat $8$ FE.

Übungs- und Lernlinks

• Erklärungen und Beispiele von brinkmann-du
• Erklärung von matheguru
• Beispiele mit Lösungen von Groolfs
• Weiteres Lernvideo, in dem ein Beispiel vorgerechnet wird

$\rightarrow$ nächste Seite ...

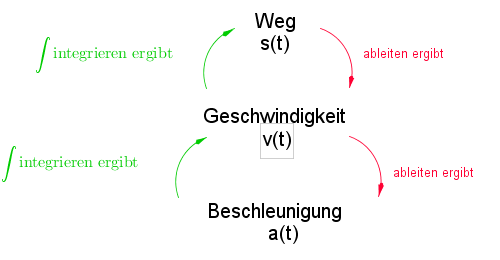
Weg, Geschwindigkeit, Beschleunigung

Wird die Geschwindigkeit $v$ durch den Graphen angegeben, so ist die Steigung die Beschleunigung $a$. Der Flächeninhalt unter $v$ gibt den Weg $s$ an.

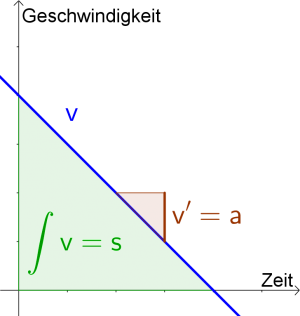
• $s(t)$ gibt den zurückgelegten Weg zum Zeitpunkt $t$ an (Einheit: $m$ oder $km$ ...)

• $v(t)$ gibt die Momentangeschwindigkeit zum Zeitpunkt $t$ an (Einheit: $m/s$ oder $km/h$ ...). Die Geschwindigkeit ist die momentane Änderung des Weges $s(t)$, d. h.

$$s'(t)=v(t)\textrm{ bzw. } \int v(t)=s(t)+c,\textrm{ wobei $c$ die Anfangsstrecke $s_0$ angibt.}$$

• $a(t)$ gibt die Beschleunigung zum Zeitpunkt $t$ an (Einheit: $m/s^2$ oder $km/h^2$ ...). Die Beschleunigung ist die momentane Änderung der Geschwindigkeit $v(t)$, d. h.

$$v'(t)=a(t)\textrm{ bzw. } \int a(t)=v(t)+c,\textrm{ wobei $c$ die Anfangsgeschwindigkeit $v_0$ angibt.}$$

Vereinfacht gesagt gilt folgender Zusammenhang:

Anwendungsbeispiel

Die ESA (European Space Agency) bringt mithilfe der Ariane 5 regelmäßig Satelliten in den Weltraum. Die Startbeschleunigung beträgt dabei ca. $5.5 m/s^2$. Gehen Sie im Folgenden davon aus, dass die Beschleunigung während des ganzen Fluges konstant ist (d. h. $a(t)=5.5 m/s^2$). Die Variable $t$ gebe die Zeit nach dem Start in Sekunden ($s$) an.

a) Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$)

b) Bestimmen Sie mithilfe von $v$ die Funktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt.

c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia).

Berechnen Sie:

• die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet.
• die Geschwindigkeit der Rakete zu diesem Zeitpunkt.

d) In etwa $36\, 000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird.

a) Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$)

Tipp zur Berechnung:

Da die Funktion der Geschwindigkeit $v(t)$ gesucht wird, müssen wir die Formel der Beschleunigung $a(t)$ einmal integrieren. Wir setzen $5.5$ (Dies entnehmen wir aus der Angabe) für $a(t)$ ein und berechnen $v(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=v_0$ wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ beträgt und damit $v(0)=0$ gelten muss.

$$v(t)=\int a(t) \cdot dt$$ $$v(t)=\int 5.5 \cdot dt$$ $$v(t)=5.5 \cdot t + v_0$$ $$v(t)=5.5 \cdot t$$

Antwort: Die Geschwindigkeitsfunktion lautet $v(t)=5.5 \cdot t$.

b) Bestimmen Sie mithilfe von $v$ die Wegfunktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt.

Tipp zur Berechnung:

Da die Funktion des Weges $s$ gesucht wird, müssen wir die Formel der Geschwindigkeit $v(t)$ einmal integrieren. Wir setzen $5.5t$ (dies entnehmen wir aus dem Ergebnis von Aufgabe a) für $v(t)$ ein und berechnen so unser Ergebnis für $s(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=s_0$ wegfällt, da unsere zurückgelegte Strecke zu Beginn $0$ ist.

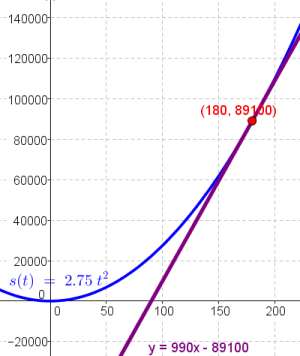
$$s(t)=\int v(t) \cdot dt$$ $$s(t)=\int 5.5t \cdot dt$$ $$s(t)=5.5 \cdot \frac{t^2}{2} +c$$ $$s(t)=2.75 \cdot t^2$$

Antwort: Die Funktionsgleichung lautet $s(t)=2.75 \cdot t^2$.

c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia).

Berechnen Sie ...

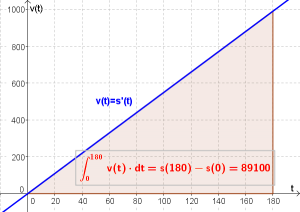
- ... die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet.

Tipp zur Berechnung:

$s(t)$ ist die Formel der zurückgelegten Strecke. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wo sich die Rakete nach $180$ Sekunden befindet.

$$s(t)=2.75 \cdot t^2$$ $$s(180)=2.75 \cdot 180^2$$ $$s(180)=89 100 m$$

Antwort: Nach $180$ Sekunden befindet sich unsere Rakete in einer Höhe von $89 100 m$.

Das $k$ der Tangente gibt die Geschwindigkeit an.

- ... die Geschwindigkeit der Rakete zu diesem Zeitpunkt.

Tipp zur Berechnung:

$v(t)$ ist die Formel, die die Geschwindigkeit zum Zeitpunkt $t$ angibt. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wie hoch die Geschwindigkeit der Rakete nach $180$ Sekunden ist. Das Ergebnis erscheint in $m/s$. Wenn das Ergebnis in $km/h$ gewünscht wäre, müsste man das Ergebnis noch mal $3.6$ rechnen.

$$v(t)=5.5 \cdot t$$ $$v(180)=5.5 \cdot 180$$ $$v(180)=990 m/s$$

$$990 m/s \rightarrow 3 564 km/h$$

Antwort: Nach $180$ Sekunden hat unsere Rakete eine Geschwindigkeit von $3 564 km/h$ erreicht.

d) In etwa $36\, 000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird.

Tipp zur Berechnung:

Die Funktion $s$ beschreibt den zurückgelegten Weg. Wenn wir die unrealistische Annahme voraussetzen, dass die Rakete „kerzengerade“ emporsteigt, müssen wir somit berechnen, wann $s(t)=36\, 000 km=36\, 000\, 000 m$ beträgt. Wichtig ist hierbei, dass $s(t)$ den Weg in $m$ angibt!

$$36\, 000\, 000=2.75 \cdot t^2$$ $$t\approx 3618.14$$

Antwort: Nach ca. $3618.14$ Sekunden erreichen wir mit unserer Rakete die Höhe $36\, 000\, 000$ Meter.

$\rightarrow$ nächste Seite ...

Wählen Sie die Technologie aus:

• GeoGebra
• TI-8x

$\rightarrow$ nächste Seite ...

Interaktive Übungen

Quiz: Bestimmtes Integral als Grenzwert (AN 4.1)

Quiz: Einfache Regeln des Integrierens (AN 4.2)

Quiz: Deutung des bestimmten Integrals (AN 4.3)

Übungs- und Maturaaufgaben

• ? $\ $ Quiz-Aufgabe (klicke links auf: "Übungen" und dann wähle eine Übung unter "Quiz")

• $Bifie$: Erddamm (leicht-mittel)

• $Bifie$: Volumenstrom (mittel-schwer-mittel)

Hier benötigst du auch Wissen über die momentane Änderungsrate und Umkehraufgaben.

• $Bifie$: Pinboard (mittel)

Hier brauchst du auch Wissen über Kurvendiskussionen und über das Lösen von Gleichungssystemen bzw. Umkehraufgaben.

• $Bifie$: Wasserkanal (mittel-mittel-leicht)

Hier brauchst du auch Wissen über Kurvendiskussionen bzw. Steigung und Steigungswinkel sowie den Flächeninhalt eines Trapezes'.

• $Bifie$: Energieverbrauch beim Joggen (mittel)

Welche Inhalte brauchst du hier noch: exponentielle Abnahme und Differenzen- und Differentialquotient.

• $Bifie$: Schmuckstück (leicht-mittel-mittel)

Was brauchst du hier noch: Quadratische Funktionen bzw. Umkehraufgaben.

• $Bifie$: Minirampe (mittel)

Hier brauchst du auch Wissen über Kurvendiskussionen sowie über Steigung und Steigungswinkel und über Umkehraufgaben.