Inhalt:Integration: Das bestimmte Integral - Berechnung der orientierten Fläche

Inhalt:Integration: Das bestimmte Integral - Berechnung der orientierten Fläche

Merke

Was wir bereits wissen: Das unbestimmte Integral $\int f(x)\cdot dx$ berechnet die Stammfunktion $F(x)$ (siehe unbestimmtes Integral ). Das bestimmte Integral bereichnet $\int_{a}^{b} f(x)\cdot dx$ bestimmt die orientierte Fläche zwischen der Kurve von $f(x)$ und der $x$-Achse in den Grenzen zwischen $a$ und $b$ (siehe Idee der Integration ). Was wir allerdings noch nicht wissen: Wie rechnen wir den Flächeninhalt nun konkret aus? Wie hängt das bestimmte Integral und das unbestimmte Integral zusammen?

Die Antwort auf beide dieser Fragen liefert ...

Der Hauptsatz der Integration

Definition

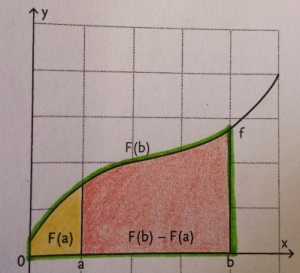
Für eine stetige Funktion $f$ gilt: Ist $F$ eine (beliebige) Stammfunktion von $f$, das heißt $F' = f$, dann gilt: $$ \int_{a}^{b} f (x)\,dx = F(x)\vert _{a}^{b} = F(b) - F(a) $$ D. h.: Die orientierte Fläche zwischen $a$ und $b$ wird berechnet, indem zuerst die Stammfunktion bestimmt wird, dann setzt man die Grenzen ein und subtrahiert nach dem Prinzip „Obere Grenze MINUS Untere Grenze“.

- $F(a)$ = gelbe Fläche
- $F(b)$ = grün-umrandete Fläche
- $F(b)-F(a)$ = rote Fläche $= \int_{a}^{b} f (x)\cdot dx $

Wiederholung der Bezeichnungen

• $f(x)$ heißt Integrand ( das, was integriert wird)
• $x$ ist die Integrationsvariable
• $a$ und $b$ sind die untere bzw. obere Integrationsgrenze
• $\int_{a}^{b} f (x)\,dx$ ist das bestimmte Integral und gibt die orientierte Fläche zwischen $f(x)$ und der $x$-Achse an

Bemerkungen:

1. $F(b)$ berechnet die orientierte Fläche zwischen $0$ und der Grenze $b$. $F(a)$ berechnet die orientierte Fläche zwischen $0$ und $a$. Somit kann die Fläche zwischen $a$ und $b$ mithilfe von $F(b)-F(a)$ bestimmt werden. So kommt man auf die Formel des 2. Hauptsatzes.
2. Wichtig ist, dass man immer zuerst die obere Grenze einsetzt und dann erst die untere Grenze. Ansonsten hat das Ergebnis das falsche Vorzeichen. $$ \int_{\color{red}{untere\ Grenze} }^{\color{red}{obere\ Grenze} } \color{green}{f(x)} \cdot \color{blue}{dx}=F(\color{red}{obere\ Grenze} )-F(\color{red}{untere\ Grenze}) $$
3. $\int_{a}^{b} f (x)$ bezeichnet die orientierte Fläche. Ist die Fläche unterhalb der $x$-Achse, so hat sie ein negatives Vorzeichen.

Dieses Video fasst noch einmal die wichtigsten Punkte zusammen (WICHTIG: bitte nur bis zur Minute 2:30 ansehen ):

Musterbeispiele

Merke

Schrittfolge zur Berechnung des bestimmten Integrals: Schritt: Ermittele die Stammfunktion $F$. Schritt: Ermittele $F(b)$ und $F(a)$ (Die Grenzen $a$ und $b$ in $F$ einsetzen). Schritt: Berechne die Differenz $F(b)-F(a)$.

$\int_{1}^{2} (6x^2 + x-2)\,dx = $

$$\int_{1}^{2} (6x^2 + x-2)\,dx =\underbrace{2x^3+\frac{x^2}{2}-2x+c\vert _{1}^{2} }_{1.\ Schritt} = \underbrace{\left[2\cdot 2^3+\frac{2^2}{2}-2\cdot 2+c\right]-\left[2\cdot 1^3+\frac{1^2}{2}-2\cdot 1+c\right]}_{2.\ Schritt}=\underbrace{(14+c) - (0.5+c) = 13.5}_{3.\ Schritt}$$

Merke

Die Integrationskante $c$ fällt bei bestimmten Integralen immer weg. Daher schreiben wir sie in Zukunft beim bestimmten Integral nicht mehr an.

$\int_{1}^{3} \left(\frac{1}{x}-\frac{2}{x^2}+\frac{3}{x^3}\right)\, dx =$

$$\int_{1}^{3} \left(\frac{1}{x}-\frac{2}{x^2}+\frac{3}{x^3}\right)\,dx = \underbrace{In\vert x\vert +\frac{2}{x}-\frac{3}{2x^2}\vert _{1}^{3} }_{1.\ Schritt}=\underbrace{ \left[In (3) + \frac{2}{3}-\frac{1}{6}\right]-\left[In (1)+2-\frac{3}{2}\right]}_{2.\ Schritt} = \underbrace{In 3 \approx 1.0986}_{3.\ Schritt}$$

Weitere Beispiele

Bestimmen Sie die Werte der folgenden bestimmten Integrale. Fertigen Se eine Skizze an, in der die berechnete Fläche eingezeichnet ist.

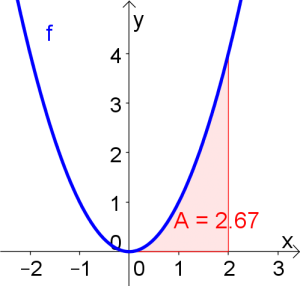
$\int\limits_{0}^{2}x^2dx$

$$\int\limits_{0}^{2}x^2dx= \frac{x^3}{3}\vert_{0}^{2} = \frac{2^3}{3}- \frac{0^3}{3} = \frac{8}{3} \approx 2.67$$

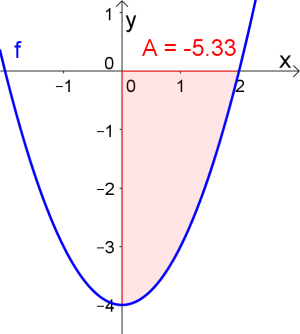
$\int\limits_{0}^{2}\left( x^2-4\right)\ dx$

$$\int\limits_{0}^{2}\left( x^2-4\right)\ dx= \frac{x^3}{3}-4x\vert_{0}^{2} =\left[\frac{2^3}{3}-4\cdot 2\right]- \left[\frac{0^3}{3}-4\cdot 0\right] = \frac{8}{3}-8 = -\frac{16}{3}\approx -5.33$$ ACHTUNG: Du erhältst ein negatives Ergebnis, weil die Fläche unterhalb der $x$-Achse ist (siehe orientierte Fläche).

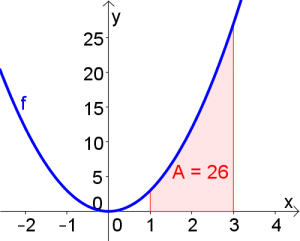
$\int\limits_{1}^{3} 3x^2dx$

$$\int\limits_{1}^{3} 3x^2dx= 3\frac{x^3}{3}\vert_{1}^{3} = 3\frac{3^3}{3}- 3\frac{1^3}{3} = 27-1 = 26$$

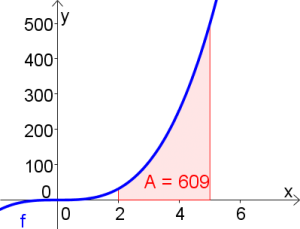
$\int\limits_{2}^{5} 4x^3dx$

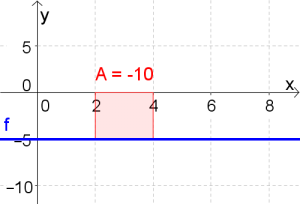
$$\int\limits_{2}^{5} 4x^3dx= 4\frac{x^4}{4}\vert_{2}^{5} = 4\frac{5^4}{4}- 4\frac{2^4}{4} = 625-16 = 609$$

$\int\limits_{2}^{4}-5dx$

$$\int\limits_{2}^{4}-5dx= -5\frac{x^1}{1}\vert_{2}^{4}=-5 \frac{4}{1}-\left(-5\frac{2}{1}\right) = -5\cdot 4 - \left(-5\cdot 2\right) = -20-(-10)=-10$$

Merke

Das bestimmte Integral gibt immer die orientierte Fläche zwischen dem Graphen und der $x$-Achse an.

Mit dieser Überlegung können auch kompliziertere Flächen berechnet werden:

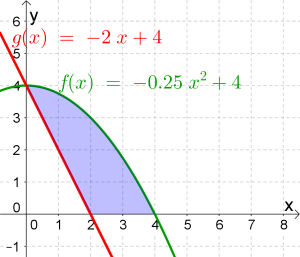
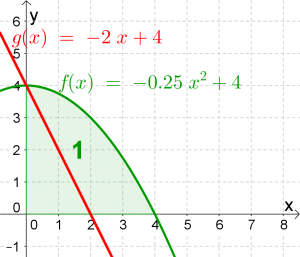
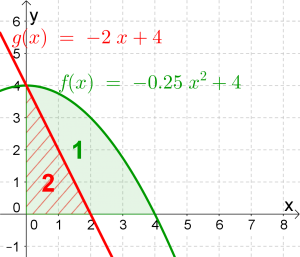
Bestimme den Inhalt der blau eingefärbten Fläche.

Da die blaue Fläche keine Fläche zwischen einem Graphen und der $x$-Achse ist, können wir sie nicht direkt berechnen. Allerdings hilft uns folgende Überlegung etwas:

• 

  Zieht man von der grünen Fläche (1) ...

• 

  .... die rote Fläche (2) ab, ...

• 

  ... so erhält man die blaue Fläche.

Damit ergibt sich die Formel: $$blaue\ Fläche=\underbrace{\int_0^4 f(x)dx}_{grüne\ Fläche}-\underbrace{\int_0^2 g(x)dx}_{rote\ Fläche}$$ $$blaue\ Fläche= \int_0^4 \left( -0.25x^2+4\right)dx-\int_0^2 \left( -2x+4\right) dx$$ Durch händische Berechnung oder mithilfe von Technologieeinsatz erhalten wir: $$blaue\ Fläche=\underbrace{10.\dot 6}_{grüne\ Fläche}-\underbrace{4}_{rote\ Fläche}=\underline{\underline{6.\dot 6} }$$

Hinweis: Selbstverständlich hätten wir die rote Fläche auch einfacher mithilfe der Flächenformel für rechtwinklige Dreiecke berechnen können.

Zusatzmaterialien

? $\ $ Übungsaufgaben zum bestimmen Integral (von Jutta Gut)

? $\ $ Übungen zum Lernen der Begriffe:

• Kreuzworträtsel
• Memory
• Hang Man