Kurvendiskussionen

Kurvendiskussionen

• Überblick und Einleitung
• Grundwissen über $f(x), f'(x)$ und $f''(x)$
• Nullstellen
• Extremstellen: Hoch- und Tiefpunkte
• Wendepunkt und Wendetangente
• Zusatzvideos zur Vertiefung
• Übungs- und Maturabeispiele

Überblick und Einleitung

Beim Thema Kurvendiskussionen geht es darum, Eigenschaften von Funktionen (bzw. Kurven) zu ermitteln. Für die Matura sind die folgenden Eigenschaften wichtig:

• Nullstellen
• Extremwerte
• Wendepunkt und Wendetangente

Wichtig: Die folgenden Inhalte gehören ebenfalls zum Thema Kurvendiskussionen, werden aber auf anderen Seiten behandelt:

• Steigung und Steigungswinkel

Grundwissen über $f(x), f'(x)$ und $f''(x)$

Die folgende Tabelle gibt dir an, was mit der Funktion $f(x)$, ihrer 1. Ableitung und ihrer 2. Ableitung berechnet werden kann.

	$f(x)$	$f'(x)$	$f''(x)$
Gibt an ...	den Funktionswert an der Stelle $x$	die Steigung von $f$ an der Stelle $x$	die Krümmung von $f$ an der Stelle $x$ ($=$ Steigung der Steigung)
physikalische Interpretation	Entfernung vom Ursprung in einem Zeit-Weg-Diagramm oder Höhe eines Objektes etc.	momentane Änderungsrate/Geschwindigkeit an der Stelle $x$	Beschleunigung an der Stelle $x$
wenn $>0$	Funktionswert ist positiv und oberhalb der $x$-Achse	$f'(x)>0 \rightarrow$ Funktion ist monoton steigend	$f''(x)>0 \rightarrow$ die Funktion ist linksgekrümmt (u-förmig), die Steigung nimmt zu
wenn $<0$	Funktionswert ist negativ und unterhalb der $x$-Achse	$f '(x)<0 \rightarrow$ Funktion ist monoton fallend	$f''(x)<0 \rightarrow$ die Funktion macht hier eine Rechtskurve (n-förmig), die Steigung nimmt ab
wenn $=0$	Nullstellen	Die Funktion steigt und fällt hier nicht. Möglicherweise befindet sich hier ein Extremum.	Möglicherweise befindet sich hier ein Wendepunkt .

Nullstellen

Im Graphen sind die drei Nullstellen $x_1, \ x_2$ und $x_3$ abgebildet.

Definition

Nullstellen sind jene Stellen (=x-Werte), an denen der Graph der Funktion die x-Achse schneidet (hier ist f(x)=0). Formale Definition: Die Funktion $f(x)$ hat bei $x_1$ eine Nullstelle, wenn gilt: $f(x_1)=0$

Video

Berechnung der Nullstellen

Um die Nullstellen zu berechnen, muss die Gleichung $f(x)=0$ gelöst werden. Je nach Funktionstyp von $f(x)$ kann entweder $x$ einfach freigestellt werden oder ein Lösungsverfahren (große Lösungformel/Quadkom, graphisches Lösungsverfahren im TR, Solve-Befehl) verwendet werden.

Als Richtwert, kannst du dir aber folgende Regel merken:

1. Bei linearen Gleichungen $0=k\cdot x+d$: nach $x$ umformen.
2. Bei quadratischen Gleichungen $0=ax^2+bx+c$: große Lösungsformel/Quadkom
3. Bei Gleichungen mit Grad $\ge 3$: graphisches Lösungsverfahren im TR

Musterbeispiele

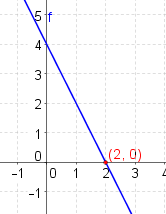
a) Bestimme die Nullstelle der linearen Funktion $f(x)=-2x+4$

Lösung: $$0=-2x+4 \ \ |-4$$ $$ -4=-2x \ \ |:(-2)$$ $$2=x$$ Antwort: Der Graph der Funktion schneidet bei $N(2|0)$ die $x$-Achse.

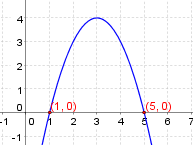
b) Bestimme die Nullstelle der quadratischen Funktion $f(x)=-x^2+6x-5$

Lösung: $$0=-x^2 + 6 \cdot x - 5$$ Nun verwenden wir die große Lösungsformel mit $a=-1$, $b=6$ und $c=-5$ $$ x_{1,2}=\frac{-b \pm \sqrt{b^2-4\cdot a\cdot c}}{2\cdot a}$$

$$x_{1,2}=\frac{-6\pm \sqrt{6^2-4\cdot (-1)\cdot (-5)}}{2\cdot (-1)}$$ $$x_{1,2}=\frac{-6\pm \sqrt{36-20}}{-2}$$ $$ x_1=\frac{-6+4}{-2}=1$$ $$ x_2=\frac{-6-4}{-2}=5$$ Antwort: Der Graph der Funktion schneidet bei $N_1(1|0)$ und $N_2(5|0)$ die $x$-Achse.

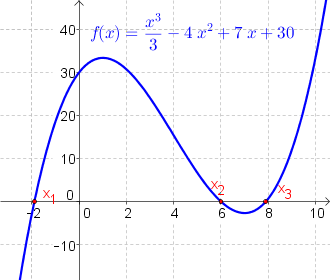
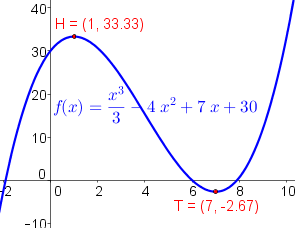
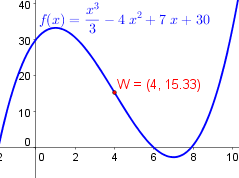
c) Bestimme die Nullstelle der kubischen Funktion $f(x)=\frac{x^3}{3}-4x^2+7x+30$ (siehe Abbildung rechts oben).

Lösung mithilfe des graphisches Lösungsverfahren im TR oder dem Löse-Verfahren (GeoGebra) $x_1=-1.9,\ x_2=6$ und $ x_3=7.9$

Extremstellen: Hoch- und Tiefpunkte

Im Graphen sind die beiden Extremstellen $x_1$ und $x_2$ samt den dazugehörenden Hoch- und Tiefpunkten eingezeichnet.

Definition

Lokale Extremstellen sind jene Stellen ($=x$-Werte), an denen der Graph der Funktion einen lokalen Hoch- oder Tiefpunkt hat. Formale Definition: Eine Funktion $f$ hat bei $x_0$ einen lokalen Hochpunkt, wenn für alle $x$ in einer Umgebung von $x_0$ gilt, dass $f(x)<f(x_0)$. (Analog funktioniert die Definition für einen lokalen Tiefpunkt.)

Video

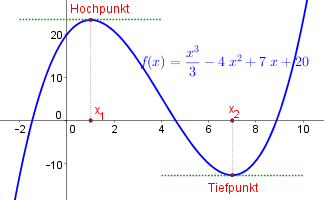
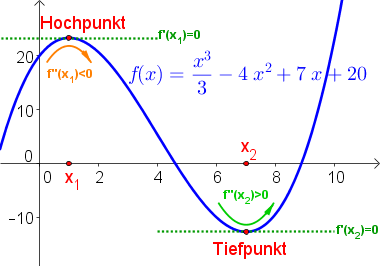
Wie am Graphen in der rechten Abbildung erkennbar ist, sind die Steigungen an den Extremstellen immer $0$ (d. h. beim Hochpunkt und Tiefpunkt steigt $f$ nicht und fällt $f$ nicht). Somit gilt $f'(x)=0$.

Zusätzlich ist der Graph beim Hochpunkt rechtsgekrümmt (d. h. $f''(x)<0$) und beim Tiefpunkt linksgekrümmt (d. h. $f''(x)>0$).

Somit erhalten wir...

Hinreichende Bedingung für ein lokales Extremum

Merke

$f'(x_0)=0$ und $f''(x_0)< 0$ $\Rightarrow\ \ \ \ $ $x_0$ ist die Stelle eines lokalen Hochpunktes (Maximums) von $f$ $f'(x_0)=0$ und $f''(x_0)>0$ $\Rightarrow\ \ \ \ $ $x_0$ ist die Stelle eines lokalen Tiefpunktes (Minimums) von $f$ $f'(x_0)=0$ und $f''(x_0)=0$ $\Rightarrow\ \ \ \ $ dann muss hier nicht unbedingt ein Extremum sein.

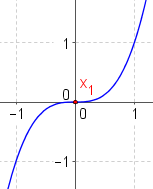
Der letzte Punkt ($f'(x_0)=0$ ABER $f''(x_0)=0$) wird klar, wenn man sich die Funktion $f(x)=x^3$ ansieht:

Beispiel für $f''(x)=0$, aber kein Extremum: $f(x)=x^3$

Graph von $f(x)=x^3$

Sei $f(x)=x^3$. Um die Extrema zu berechnen, setzen wir $f'(x)=0$ und bestimmen dann $f''(x)$ an dieser Stelle:

$f'(x)=3x^2$ $0=3x^2$ $\rightarrow x=0$

$\ $ und $\ \ \ \ $

$f''(x)=6x$ $f''(0)=0$

Somit ist $f'(0)=0$ und $f''(0)=0$. Wie man aber leicht am Graphen erkennt, ist bei $x_1=0$ kein Extremum (weder Hoch- noch Tiefpunkt).

Die Bedingungen $f''(x_0)<0$ (für ein Maximum) und $f''(x_0)>0$ (für ein Minimum) sind also wichtig.

Musterbeispiel

Bestimme die Extrema der Funktion $\ f(x)=\frac{x^3}{3}-4x^2+7x+30$.

Lösung:

Zuerst bestimmen wir die 1. Ableitung $f'(x)$ und die zweite Ableitung $f''(x)$: $$f(x)=\frac{x^3}{3}-4x^2+7x+30$$ $$f'(x)=x^2-8x+7$$ $$f''(x)=2x-8$$

Nun setzen wir die 1. Ableitung $0$ (da die Steigung bei Hoch- und Tiefpunkt $0$ ist): $$0=x^2-8x+7$$ $$x_{1,2}=\frac{8\pm \sqrt{64-4\cdot 7} }{2}$$ $$x_{1,2}=\frac{8\pm 6}{2}$$ $$x_1=1$$ $$x_2=7$$

Graph mit Hoch- und Tiefpunkt

Somit haben wir $2$ mögliche Extremstellen gefunden. Nun müssen wir noch überprüfen, ob es sich um Hoch- oder Tiefpunkte (oder weder noch) handelt. Hierzu setzen wir $x_1=1$ und $x_2=7$ in die zweite Ableitung ein:

$f''(1)=2\cdot 1-8=-6<0 \rightarrow $ rechtsgekrümmt $\rightarrow$ Hochpunkt

$f''(7)=2\cdot 7-8=+6>0 \rightarrow $ linksgekrümmt $\rightarrow$ Tiefpunkt

Somit wissen wir, dass sich bei $x=1$ ein Hochpunkt und bei $x=7$ ein Tiefpunkt befindet. Zuletzt bestimmen wir nun noch die $y$-Koordinaten des Hoch- und Tiefpunktes. Hierzu setzen wir die $x$-Werte in die ursprüngliche Funktion $f(x)$ ein:

$f(1)=\frac{1^3}{3}-4\cdot 1^2+7\cdot 1+30=33.33\rightarrow H(1\vert 33.33)$

$f(7)=\frac{7^3}{3}-4\cdot 7^2+7\cdot 7+30=-2.67\rightarrow T(7\vert -2.67)$

Interaktive Übungen

Quiz: Extremstellen von Funktionen (FA 1.5 und AN 3.3)

Wendepunkt und Wendetangente

Funktion mit Wendepunkt W und Wendetangente

Definition

$ $ Ein Wendepunkt ist ein Punkt, in dem die Funktion f ihr Krümmungsverhalten ändert. Das heißt: Die Funktion geht von einer Rechtskrümmung in eine Linkskrümmung über (oder umgekehrt). Die Tangente durch den Wendepunkt heißt Wendetangente.

Wie erkennt man einen Wendepunkt?

Stell dir vor, der Graph ist eine Straße und du würdest die Straße mit einem Auto von links nach rechts entlangfahren. Zuerst kommt eine Rechtskurve, in der du das Lenkrad nach rechts drehst. Anschließend kommt eine Linkskurve, in der du das Lenkrad nach links drehen musst. Genau zwischen der Rechts- und der Linkskurve gibt es einen Moment, in dem das Lenkrad gerade ist - das ist der Wendepunkt.

Hinreichende Bedingung für einen Wendepunkt

Merke

Die Funktion $f(x)$ hat bei $x_0$ einen Wendepunkt, wenn gilt: $f''(x_0)=0 \quad$ UND $f'''(x)\ne 0$

Video

Musterbeispiel

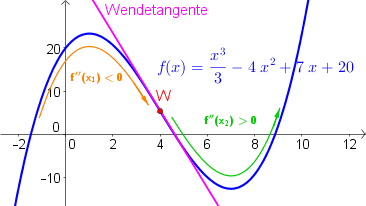
Bestimme den Wendepunkt und die Wendetangente der Funktion $\ f(x)=\frac{x^3}{3}-4x^2+7x+30$.

1. Wendepunkt

Zuerst bestimmen wir die zweite Ableitung $f''(x)$ und die dritte Ableitung $f'''(x)$: $$f(x)=\frac{x^3}{3}-4x^2+7x+30$$ $$f'(x)=x^2-8x+7$$ $$f''(x)=2x-8$$ $$f'''(x)=2$$

Nun setzen wir die zweite Ableitung $= 0$:

$$f''(x)=2x-8$$ $$0=2x-8$$ $$x=4$$

Somit ist die Stelle $x=4$ ein möglicher Wendepunkt. Um zu überprüfen, ob es sich wirklich um einen handelt, müssen wir den $x$-Wert in die dritte Ableitung einsetzen:

Graph mit Wendepunkt

$$f'''(x)=2$$ Da die dritte Ableitung konstant $=2$ ist (d. h. für alle $x$ den Wert $2$ hat), gilt insbesondere $$f'''(4)=2\ne 0$$ Somit ist an der Stelle $x=4$ ein Wendepunkt.

Um die $y$-Koordinate des Wendepunktes zu bestimmen, setzen wir in die ursprüngliche Funktion $f(x)$ ein, und erhalten: $$f(4)=\frac{4^3}{3}-4\cdot4^2+7\cdot 4+30=15.33$$

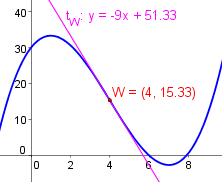
Somit hat der Wendepunkt die Koordinaten $W(4|15.33)$.

2. Wendetangente

$\rightarrow$ Siehe hier auch: Bestimmen der Tangente

Um die Wendetangente $t_W: y=k\cdot x+d$ zu berechnen, brauchen wir zwei Sachen:

1. den Wendepunkt (diesen haben wir schon zuvor berechnet: $W(4|15.33)$)
2. die Steigung der Wendetangente - diese berechnen wir jetzt:

Die Steigung $k$ der Wendetangente ist ident mit der Steigung der Funktion am Wendepunkt. Somit müssen wir die Steigung von $f(x)$ beim Wendepunkt $W(4|15.33)$ berechnen und dies macht man immer mit der 1. Ableitung $f'(x)$:

$$f'(x)=x^2-8x+7$$ $$f'(4)=4^2-8\cdot 4+79$$ $$f'(4)=-9$$

Somit ist $k=-9$

Graph mit Wendepunkt und Wendetangente

Um das $d$ zu berechnen, setzen wir nun $k=-9$ und die Koordinaten des Wendepunktes $W(\underbrace{4}_{x}|\underbrace{15.33}_{y})$ in die $y=kx+d$-Darstellung und erhalten: $$y=kx+d$$ $$15.33=-9\cdot 4+d$$ $$d=51.33$$

Somit lautet die Gleichung der Wendetangente: $$\underline{\underline{t_W: \ y=-9\cdot x+51.33}}$$

Merke

Maximale oder minimale Steigung Am Wendepunkt befindet sich ein lokales Extremum der Steigung $f'(x)$. Das bedeutet, dass am Wendepunkt sich entweder a) ein lokales Maximum der Steigung (der Graph ist hier (in einem Bereich) am steilsten) oder b) ein lokales Minimum der Steigung (der Graph ist hier (in einem Bereich) am flachsten) befindet. Begründung: Am Wendepunkt gilt für die erste Ableitung von $f'$: $$(f'(x))'=f''(x)=0)$$ und für die zweite Ableitung von $f'$: $$(f'(x))''=f'''(x)\neq 0$$ Somit hat $f'$ hier einen Hoch- oder Tiefpunkt.

Zusatzvideos zur Vertiefung

Quiz: Beschreiben von Eigenschaften mithilfe von Ableitungsfunktionen (AN 3.3)

Musterbeispiele und Übungen

• Musterbeispiel von Jutta Gut
• Musterbeispiel von "Matheguru"
• ? Quiz zu Kurvendiskussionen (mathe-online)
• ? Online-Übung zu Kurvendiskussionen (GeoGebra) WICHTIG

• ? Online-Rechner zu Kurvendiskussionen (MatheGuru)

Matura-Aufgaben

1. $Bifie$: Steinschleuder (Bifie-Aufgabe: mittel)

   Welche Inhalte brauchst du hier noch: Differentialquotient

2. $Bifie$: Zylindrische Gefäße (Bifie-Aufgabe: mittel-leicht-leicht)
3. $Bifie$: Tagestemperatur (Bifie-Aufgabe: leicht-leicht-mittel)
4. $Bifie$: Geländewagen (Bifie-Aufgabe: schwer-mittel-schwer)

   Welche Inhalte brauchst du hier noch: Differenzenquotient

5. $Bifie$: Hefepilz (Bifie-Aufgabe: mittel-leicht-mittel)
6. $Bifie$: Straßenbahn (Bifie-Aufgabe: mittel-leicht-mittel)
7. $Bifie$: Simulation eines Golfballflugs (Bifie-Aufgabe: leicht-mittel-mittel-schwer)

   Hier brauchst du auch Wissen über Steigung und Steigungswinkel

8. $Bifie$: Skispringen (Bifie-Aufgabe: leicht-mittel-mittel)

   Welche Inhalte brauchst du hier noch: Quadratische Funktionen und Bewegungsaufgaben - Weg/Geschwindigkeit/Beschleunigung

9. $Bifie$: Kugelstoßen (leicht-mittel-mittel)

   siehe hier auch das Thema Steigung und Steigungswinkel

10. $Bifie$: Minirampe (mittel)

    Hier brauchst du auch Wissen über Integration (Aufgabe a) sowie über Steigung und Steigungswinkel und über Umkehraufgaben (Aufgabe d)

11. $Bifie$ : Leistungskurve

    Hier musst du die Ableitungsfunktion graphisch bestimmen.