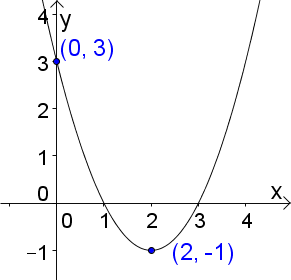Quadratische Funktionen

Quadratische Funktionen

• Einleitung
• Graph, Parameter und Eigenschaften
• Nullstellen quadratischer Funktionen
• Rechenbeispiel
• Scheitelpunktform
• Funktionsgleichung bestimmen
• Matura-Beispiele

Abbildung zweier Parabeln samt zugehörigen Funktionsgleichungen

Definition

Die Funktionsgleichung einer quadratischen Funktion (auch Polynomfunktion 2. Grades genannt) lautet $$y=a\cdot x^2+b\cdot x+c$$ mit $a,b,c\in$ $\mathbb{R} $ und $a\neq 0$.

Hinweis:

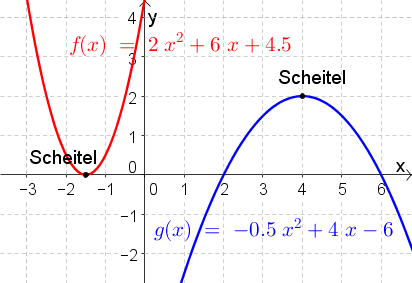
• Wichtig: Der Graph einer quadratischen Funktion ist IMMER eine Parabel und damit $\cup$- oder $\cap$-förmig (siehe Abbildungen rechts).

• Quadratische Funktionen haben immer genau einen Hoch- oder Tiefpunkt. Diesen nennt man Scheitelpunkt (oder kurz Scheitel).

• Die Gleichung $ y=a\cdot x^2+b\cdot x+c$ wird als Normalform bezeichnet (sozusagen: im Normalfall ist die Funktion in dieser Form gegeben).

Neben der Normalform gibt es auch noch die Scheitelpunktform $y=a\cdot (x-w)^2+s$

$\rightarrow$ nächste Seite ...

Graph, Parameter und Eigenschaften

$Aha!$ $\ $ Schau dir dieses Arbeitsblatt an und beantworte die darin angeführten Fragen.

Gegeben sei eine quadratische Funktion der Form $$f(x)= a\cdot x^2+b\cdot x+c$$

Dann haben die Parameter $a,\ b$ und $c$ folgende Auswirkungen auf den Graphen der quadratischen Funktion:

---

$a$ gibt an, wie stark der Graph steigt oder fällt

• Ist $a>0$, so ist die Parabel nach oben offen.
• Ist $a<0$, so ist die Parabel nach unten offen.
• Je größer $|a|$ ist, desto steiler ist der Graph.
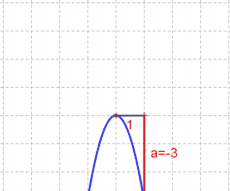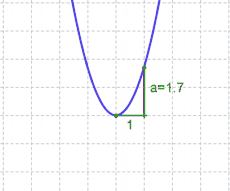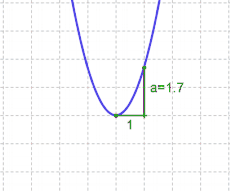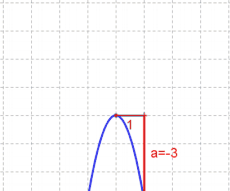
• $a$ kann abgelesen werden, indem man vom Scheitelpunkt aus eins nach rechts und dann senkrecht zum Graphen geht.

Achtung: Im Gegensatz zu den linearen Funktionen darf man hier immer nur $1$ nach rechts, niemals mehr. Der Grund: Die Steigung der Parabel ändert sich, sie wird immer steiler. Dagegen ist die Steigung der Linearen Funktion immer konstant. Allgemein gilt: Ist eine Steigung konstant, so ist es egal, ob man z. B. $1$ nach rechts und $3$ hinauf, oder $2$ nach rechts und $6$ hinauf geht.

---

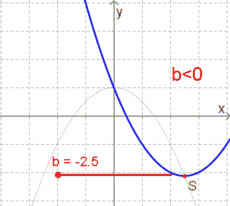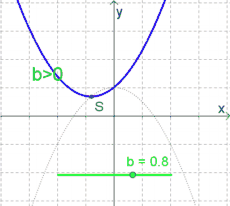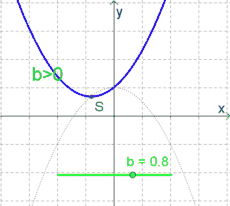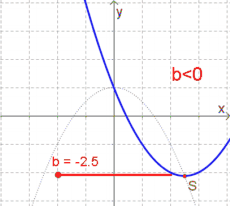
$b$ verschiebt den Scheitelpunkt entlang einer Kurve nach rechts oder links:

Ist $a>0$, so gilt:

• Ist $b<0$, so liegt der Scheitelpunkt rechts (!) der $y$-Achse.
• Ist $b>0$, so liegt der Scheitelpunkt links (!) der $y$-Achse.
• Ist $b=0$, so liegt der Scheitelpunkt genau auf der $y$-Achse. Der Funktionsgraph ist dadurch symmetrisch zur $y$-Achse.

Ist dagegen $a<0$, so bewirkt $b<0$ eine Verschiebung nach links und $b>0$ eine Verschiebung nach rechts (also genau umgekehrt zu $a>0$).

Merke: Für $a>0$:

• $b<0\rightarrow$ rechts
• $b>0\rightarrow$ links

Ist $a<0$, dann ist es genau umgekehrt.

Zusatz für Interessierte

Die Kurve, entlang derer die Parabel verschoben wird, ist die Spiegelung der Parabel parallel zur $x$-Achse.

Wer selbstständig beweisen kann, warum dies so ist, dem ist der 1er so gut wie sicher.

---

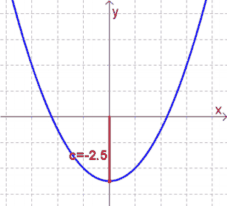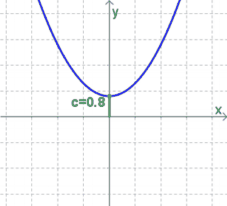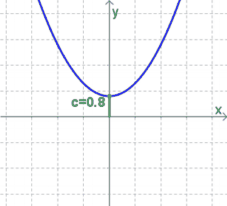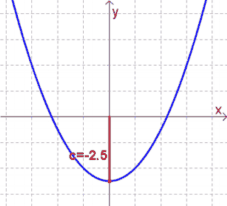
$c$ gibt den Schnittpunkt mit der $y$-Achse an (vgl. das $d$ bei den linearen Funktionen):

• Ist $c>0$, so liegt der Schnittpunkt oberhalb der $x$-Achse.
• Ist $c=0$, so geht die Parabel durch den Koordinatenursprung.
• Ist $c<0$, so schneidet die Parabel die $y$-Achse unterhalb der $x$-Achse.

Zusammenfassung über die Verschiebung einer quadratischen Funktion

$\rightarrow$ nächste Seite ...

Nullstellen quadratischer Funktionen

Parabeln mit $0, 1$ oder $2$ Nullstellen

Die Nullstellen einer quadratischen Funktion sind die Schnittpunkte der Parabel mit der $x$-Achse.

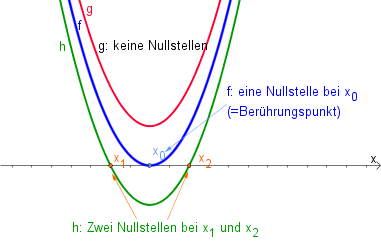
Je nachdem, wie die Parabel im Koordinatensystem liegt gibt es:

• $2$ Nullstellen
• $1$ Nullstelle ($=$ Scheitelpunkt liegt auf der $x$-Achse)
• $0$ Nullstellen.

Die Nullstellen einer quadratischen Funktion werden berechnet, indem man $f(x)=0$ setzt und dann die quadratische Gleichung $$0=a\cdot x^2+b\cdot x+c$$ löst.

$\rightarrow$ siehe auch unter Quadratische Gleichungen

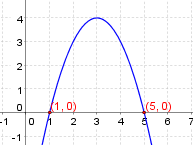
Bestimme die Nullstelle der quadratischen Funktion $f(x)=-x^2+6x-5$

Zuerst setzen wir $f(x)=0$:

$$0=-x^2 + 6 \cdot x - 5$$ Nun verwenden wir ein Lösungsverfahren, um die quadratische Gleichung zu lösen. Hier als Beispiel verwenden wir große Lösungsformel mit $a=-1$, $b=6$ und $c=-5$ $$ x_{1,2}=\frac{-b \pm \sqrt{b^2-4\cdot a\cdot c} }{2\cdot a}$$

$$x_{1,2}=\frac{-6\pm \sqrt{6^2-4\cdot (-1)\cdot (-5)} }{2\cdot (-1)}$$ $$x_{1,2}=\frac{-6\pm \sqrt{36-20} }{-2}$$ $$ x_1=\frac{-6+4}{-2}=1$$ $$ x_2=\frac{-6-4}{-2}=5$$ Antwort: Der Graph der Funktion schneidet bei $N_1(1\vert 0)$ und $N_2(5\vert 0)$ die $x$-Achse.

$\rightarrow$ nächste Seite ...

Typische Rechenbeispiele bei gegebener Funktionsgleichung

Ein Ball wird in die Höhe geworfen. Die Funktion $h(t)=-0.1t^2+0.3t+3$ gibt die Höhe des Balles in Metern ($m$) nach $t$ Sekunden ($s$) an.
$\ $a) Bestimmen Sie die Abwurfhöhe des Balles.

b) Ermitteln Sie die Höhe des Balles nach $6$ Sekunden.

c) Berechnen Sie, zu welchem Zeitpunkt der Ball auf dem Boden aufkommt.

d) Ermitteln Sie, zu welchem Zeitpunkt der Ball eine Höhe von $2 m$ hat.

e) Skizzieren Sie den Graphen von $h(t)$ im Intervall $[-2;8]$.

f) Erklären Sie, wie mithilfe der Nullstellen der Funktion $h(t)$ jener Zeitpunkt bestimmt werden kann, bei dem der Ball seine maximale Höhe erreicht.

a) Es gilt $$h(t)=-0.1t^2+0.3t+3$$ Bereits an $c=3$ erkennt man, dass die Anfangshöhe 3$m$ ist. Alternativ kann man auch für $t=0$ einsetzen (da hier der Beginn ist):

$$h(0)=-0.1\cdot 0^2+0.3\cdot 0+3$$ $$h(0)=3$$

b) Laut Angabe ist $t=6$. Setzen wir dies in die Funktionsgleichung ein, so erhalten wir: $$h(6)=-0.1\cdot 6^2+0.3\cdot 6+3$$ $$h(6)=1.2\ m$$

c) Gesucht ist die Nullstelle der Funktion. D. h. für welches $t$ gilt, dass $h(t)=0$ ist: $$0=h(t)$$ $$0=-0.1t^2+0.3t+3$$ Nun löst man die Gleichung z. B. mit der großen Lösungsformel oder mit dem Löse-Befehl und erhält: $$t_1=-4.18\ \ \ \textrm{ und }\ \ \ t_2=7.18$$ Der Ball landet nach $7.18 s$ auf dem Boden.

d) Für welches $t$ ist $h(t)=2$? $$2=h(t)$$ $$2=-0.1t^2+0.3t+3\ \ \ \vert -2$$ $$0=-0.1t^2+0.3t+1$$ Nun löst man die Gleichung z. B. mit der großen Lösungsformel oder mit dem Löse-Befehl und erhält: $$t_1=-2\ \ \ \textrm{ und }\ \ \ t_2=5$$ Somit hat der Ball nach $5$ Sekunden eine Höhe von $2 m$.

e)

Graph der Funktion $h(t)$

f) Nach c) lauten die Nullstellen $t_1=-4.18$ und $t_2=7.18$. Da die Parabel symmetrisch zum Scheitelpunkt ist und die Parabel nach unten offen ist ($a=-0.1<0$), liegt der Scheitelpunkt/Hochpunkt genau zwischen den beiden Nullstellen: $t_{max}=\frac{-4.18+7.18}{2}=1.5$

Nach $1.5 s$ erreicht der Ball seine maximale Höhe.

$\rightarrow$ nächste Seite ...

Scheitelpunktform

Allgemein

Neben der Normalform ($f(x)=ax^2+bx+c$) gibt es auch noch die sogenannte Scheitelpunktform der Parabel: $$\textrm{Scheitelpunktform: } f(x)=a\cdot (x-w)^2+s$$

$a$... gibt die Steigung (genauso wie bei der Normalform) an

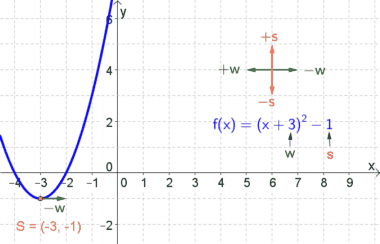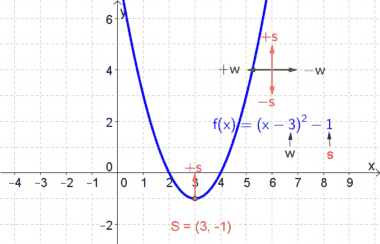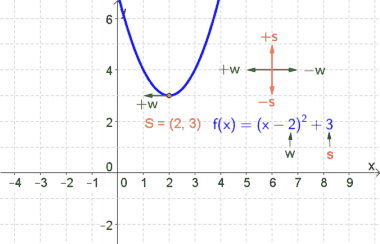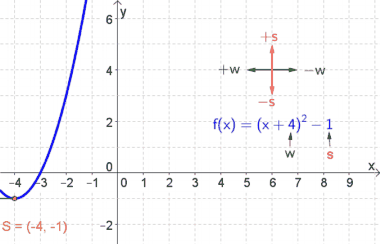
$w$... waagrechte Verschiebung des Scheitelpunktes vom Ursprung

$s$... senkrechte Verschiebung des Scheitelpunktes vom Ursprung

$Aha!$ $\ $ In diesem diesem Arbeitsblatt kannst du die Bedeutung der Scheitelpunktform genauer lernen.

? $\ $ Und hier findest du eine Aufgabe zur Scheitelpunktform.

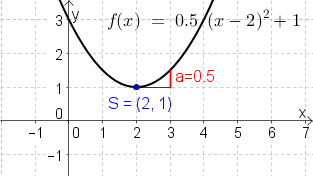
Musteraufgabe: Zeichnen Sie den Graphen der Funktion $f(x)=0.5\cdot (x-2)^2+1$ in ein Koordinatensystem. Wählen Sie dabei einen passenden Maßstab.

Lösung:

• $w=-2$... Somit wird die Parabel um $2$ nach rechts verschoben.
• $s=1$... Somit wird die Parabel um $1$ hinauf verschoben.
• Der Scheitelpunkt $S$ hat folglich die Koordinaten $S(2|1)$.
• $a=0.5$... damit erhält man die Steigung, wenn man $1$ nach rechts und $0.5$ hinauf geht.

Vorteil der Scheitelpunktform

Die Scheitelpunktform hat den Vorteil, dass

a) bei gegebener Funktionsgleichung direkt die Koordinaten des Scheitelpunktes bestimmt werden können bzw.

b) bei gegebenem Graphen direkt mithilfe des Scheitelpunktes $w$ uns $s$ bestimmt werden können.

Umwandlung von der Scheitelpunktform $y=a\cdot (x+w)^2+s$ in die Normalform $y=ax^2+bx+c$

Methode: Quadriere die Klammer aus und vereinfache den Term.

Gegeben ist die quadratische Funktion $f(x)=0.5\cdot (x-2)^2+1$ in Scheitelpunktform.

a) Bestimmen Sie die Koordinaten des Scheitelpunktes.

b) Wandeln Sie die Funktion in die Normalform $f(x)=ax^2+bx+c$ um.

a) $S(2\vert 1)$, da die Parabel $1$ hinauf ($1=s$...senkrecht) und $2$ nach rechts ($-2=w$...waagrecht) verschoben wurde.

b) Wir quadrieren die Klammer aus und vereinfachen (siehe Binomische Formeln): $$f(x)=0.5\cdot (x-2)^2+1$$ 1. Schritt: Ausquadrieren $$f(x)=0.5\cdot (x^2-4x+4)+1$$ 2. Schritt: Vereinfachen $$f(x)=0.5x^2-2x+2+1$$ $$f(x)=0.5x^2-2x+3$$ Die Normalform von $f$ lautet $\underline{\underline{f(x)=0.5x^2-2x+3} }$.

Umwandlung von der Normalform in die Scheitelpunktform

Methode: Um von der Normalform auf die Scheitelpunktform zu kommen, muss man den Funktionsterm quadratisch ergänzen.

Gegeben ist eine quadratische Funktion in Normalform: $f(x)=x^2-2x+3$. Bestimmen Sie die Koordinaten des Scheitelpunktes, indem sie die Funktionsgleichung zuerst in die Scheitelpunktform umformen.

Quadratisches Ergänzen bedeutet, den Funktionsterm so umzuformen, bis eine binomische Formel entsteht:

$$f(x)=x^2-2x+3$$ $$f(x)=x^2-(2\cdot 1)\cdot x+3$$ $$f(x)=x^2-2\cdot 1\cdot x+(1+2)$$ $$f(x)=(x^2-2\cdot 1\cdot x+1)+2$$ Nun die binomische Formel $a^2+2ab+b^2=(a+b)^2$ verwenden: $$\underline{\underline{f(x)=(x-1)^2+2} }$$ Somit haben wir die Scheitelpunktform $f(x)=(x-1)^2+2$ und die Koordinaten des Scheitelpunktes lauten: $(1\vert 2)$ ($s=1$ und $w=+1\rightarrow$ 1 nach rechts)

Füge im folgenden Applet zu jeder Graphik die passende Funktion hinzu.

$\rightarrow$ nächste Seite ...

Funktionsgleichung bestimmen

Typische Aufgabenstellung:
Bestimmen Sie die Funktionsgleichung der quadratischen Funktion, wenn mehrere Punkte auf der Parabel ($=$ Graph der quadratischen Funktion) gegeben sind.

Lösungsweg: Je nachdem, ob der Scheitelpunkt gegeben ist, gibt es zwei verschiedene Lösungswege.

a) Wenn der Scheitelpunkt gegeben ist, verwendet man die Scheitelpunktform und bestimmt anhand der Koordinaten des Scheitelpunktes $w$ und $s$ und anschließend $a$.

b) Wenn der Scheitelpunkt nicht gegeben ist, verwendet man die Normalform und stellt mithilfe von $3$ Punkten insgesamt $3$ Gleichungen auf, indem man die Punkte in die Funktionsgleichung $y=a\cdot x^2+b\cdot x+c$ einsetzt.

Musterbeispiel

Normalform $y=a\cdot x^2+b\cdot x+c$	Scheitelpunktform $ y=a\cdot(x-w)^2+s$
Wird verwendet, wenn: Scheitelpunkt nicht bekannt ist $3$ Punkte auf dem Graphen bekannt sind Nullstellen berechnet werden müssen	Wird verwendet, wenn: Scheitelpunkt bekannt oder ablesbar ist
Berechnung der Parameter Man bestimmt $3$ Punkte des Graphen und setzt sie in die Funktionsgleichung ein. Das daraus entstehende Gleichungssystem wird gelöst.	Berechnung der Parameter $w$ und $s$ können mithilfe des Scheitelpunktes $S=(w,s)$ bestimmt werden. $a$ erhält man, indem man einen weiteren Punkt aus dem Graphen in die Funktionsgleichung einsetzt oder $a$ aus dem Graphen abliest (eins nach rechts, $a$ hinauf/hinab).
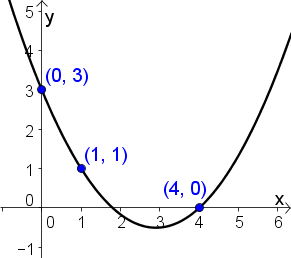
Typische Aufgabenstellung: Bestimmen Sie die Funktionsgleichung der abgebildeten Graphen.
Da der Scheitelpunkt nicht bekannt ist, setzen wir die drei Punkte in die Normalform $y=a\cdot x^2+b\cdot x+c$ ein: $$(0,3)\rightarrow \ 3=a\cdot 0^2+b\cdot 0+c$$ $$ (1,1)\rightarrow\ 1=a\cdot 1^2+b\cdot 1+c$$ $$ (4,0)\rightarrow\ 0=a\cdot 4^2+b\cdot 4+c$$ Daraus ergibt sich das folgende Gleichungssystem: $$I:\ 0\cdot a+0\cdot b+c=3$$ $$II: \ 1\cdot a+1\cdot b+c=1$$ $$III:\ 16\cdot+4\cdot b+c=0$$ Löst man dieses, so erhält man: $a=0.42,\ b=-2.42$ und $c=3$ $$\rightarrow \underline{\underline{y=0.42x^2-2.24x+3}}$$	Der Scheitelpunkt hat die Koordinaten $S(2|-1)$. Somit gilt: $w=2$, da der Graph um $2$ nach rechts verschoben wurde. $s=-1$, da der Graph um 1 hinunter verschoben wurde. $$\rightarrow y=a\cdot(x-2)^2-1$$ Um $a$ zu berechnen, setzen wir nun den Punkt $(0\vert 3)$ ein und erhalten: $$3=a\cdot (0-2)^2-1$$ $$3=a\cdot 4-1$$ $$4=4\dot a$$ $$a=1$$ $$\rightarrow \underline{\underline{y=1\cdot(x-2)^2-1}}$$ Hinweis: Dass $a=1$ ist, wäre auch einfacher aus dem Graphen ablesbar gewesen.

Online-Übung zur Bestimmung der Funktionsgleichung

Bestimme die Funktionsgleichung der Quadratischen Funktion mit $f(x)=ax^2+bx+c$ mithilfe der gegebenen Punkte.

• ? : Weitere Übung zur Bestimmung der Funktionsgleichung in Normalform

$\rightarrow$ nächste Seite ...

Matura-Beispiele

• $Bifie$: Wasserstrahl (Bifie-Aufgabe: mittel-mittel-leicht)

  Welche Inhalte werden hier noch gefragt: Nullstelle

• $Bifie$: Laptops (Bifie-Aufgabe: mittel-leicht-leicht)

  Siehe auch: Quadratische Gleichungen

• $Bifie$ : Bungeejumping (leicht-mittel-mittel)

  Für Aufgabe b) brauchst du den Differenzen- und Differentialquotient (erst in der 4. Klasse).

• $Bifie$: Skispringen (leicht-mittel-mittel)

  Aufgabe b) benötigt Wissen über Kurvendiskussionen

• $Bifie$: Ortsumfahrung (Bifie-Aufgabe: mittel-mittel)

  Für Aufgabe a) musst du wissen, wie du die Tangentengleichung bestimmen kannst.