Quadratische Gleichungen

Quadratische Gleichungen

Definition

Quadratische Gleichungen sind Gleichungen der Form $$0=a\cdot x^2+b\cdot x+c$$ mit $a,\ b,\ c\in \mathbb{R}$, wobei $a\neq 0$ ist.

Beispiele:

• $0=4x^2-3x+10$ (hier ist $a=4,\ b=-3$ und $c=10$)
• $0=x^2-1$ (hier ist $a=1,\ b=0$ und $c=-1$)

Lösung der allgemeinen Form - die große Lösungsformel

Eine quadratische Gleichung kann in der Regel nicht durch einfaches Umformen gelöst werden (außer es handelt sich um einen Sonderfall (siehe unten)).

Stattdessen verwendet man hier die große Lösungsformel:

Merke

Die große Lösungsformel Gegeben ist eine quadratische Gleichung der Form $0=a\cdot x^2+b\cdot x+c$. Dann lassen sich die beiden Lösungen mit der folgenden Formel berechnen: $$x_{1,2}=\frac{-b\pm \sqrt{b^2-4\cdot a\cdot c} }{2\cdot a}$$ wobei $x_1=\frac{-b- \sqrt{b^2-4\cdot a\cdot c} }{2\cdot a}$ die erste Lösung und $x_2=\frac{-b+ \sqrt{b^2-4\cdot a\cdot c} }{2\cdot a}$ die zweite Lösung der Gleichung ist.

Merke

Eine quadratische Gleichung hat maximal $2$ Lösungen (siehe unten: Lösungsmöglichkeiten)

Hinweis:

• Der Solve-Befehl eignet sich im Allgemeinen NICHT für quadratische Gleichungen, da der Solve-Befehl nur eine Lösung anzeigt.
• Mit GeoGebra kann der Löse-Befehl verwendet werden.

Löse die Gleichung $12=-2x^2+12x+2$

Zuerst formen wir die Gleichung um, dass auf einer Seite $0$ steht:

$0=-2x^2 + 12 \cdot x - 10$
Nun verwenden wir die große Lösungsformel mit $a=-2, b=12$ und $c=-10 \ ^*$

$\begin{align} x_{1,2}&=\frac{-b \pm \sqrt{b^2-4\cdot a\cdot c} }{2\cdot a} \\ x_{1,2}&=\frac{-12\pm \sqrt{12^2-4\cdot (-2)\cdot (-10)} }{2\cdot (-2)} \\ x_{1,2}&=\frac{-12\pm \sqrt{144-80} }{-4} \\ x_1&=\frac{-12+8}{-4}=1 \\ x_2&=\frac{-12-8}{-4}=5 \end{align}$

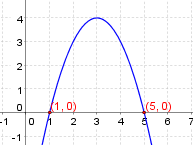
Antwort: Die Lösungsmenge lautet $\mathbb{L}= \left\{1, 5 \right\}$. Die Lösungen können als Nullstellen der zugehörigen Funktion gedeutet werden (siehe Abb. rechts).

$ ^* $ An dieser Stelle könnte die gesamte Gleichung auch durch $(-2)$ dividiert werden und die äquivalente Gleichung $0=x^2 - 6 \cdot x + 5$ mit Hilfe der kleinen Lösungsformel ($p$-$q$-Formel) gelöst werden (siehe unten).

Lösung von Gleichungen der Form $x^2+b \cdot x +c=0$

Diese Gleichungen unterscheiden sich von der allgemeinen Form dadurch, dass stets $a=1$ ist. Jede quadratische Gleichung kann auf diese Form gebracht werden, indem man durch den Koeffizienten $a$ dividiert! Der Vorteil beim Lösen einer solchen Gleichung ist, dass die Lösungsformel deutlich einfacher (und somit leichter zu merken) ist. Man nennt diese Formel kleine Lösungsformel. Aus historischen (und musikalischen) Gründen werden anstelle der Variablen $b$ und $c$ die Variablen $p$ und $q$ verwendet.

Merke

Die kleine Lösungsformel Gegeben ist eine quadratische Gleichung der Form $0=x^2+p\cdot x+q$. Dann lassen sich die beiden Lösungen mit der folgenden Formel berechnen: $$x_{1,2}= - \frac{p}{2} \ \pm \ \sqrt{ {\left(\frac{p}{2} \right)}^2 -q }$$ wobei $x_1= - \frac{p}{2} \ + \ \sqrt{ {\left(\frac{p}{2} \right)}^2 -q } \ $ die erste Lösung und $x_2= - \frac{p}{2} \ - \ \sqrt{ {\left(\frac{p}{2} \right)}^2 -q } \ $ die zweite Lösung der Gleichung ist.

Musterbeispiel: Löse die Gleichung $12=-2x^2+12x+2$ nun mithilfe der kleinen Lösungsformel.

Lösung: Zuerst formen wir die Gleichung um, dass auf einer Seite $0$ steht:

$$0=-2x^2 + 12 \cdot x - 10$$ Damit wir die kleine Lösungsformel anwenden dürfen, müssen wir die Gleichung noch durch $(-2)$ dividieren und erhalten $$0=x^2 - 6 \cdot x + 5$$ Hier können wir nun die kleine Lösungsformel mit $p=-6$ und $q=5$ anwenden. \begin{align} x_{1,2}&= - \frac{p}{2} \ \pm \ \sqrt{ {\left(\frac{p}{2} \right)}^2 -q } \\ x_{1,2}&= - \frac{-6}{2} \ \pm \ \sqrt{ {\left(\frac{-6}{2} \right)}^2 -5 } \\ x_{1,2}&=3 \pm \sqrt{9-5} \\ x_1&=3+2=5 \\ x_2&=3-2=1 \end{align}

Antwort: Die Lösungsmenge lautet wiederum $\mathbb{L}= \left\{1, 5 \right\}$.

Sonderfall: $0=a\cdot x^2+b\cdot x$

In diesem Fall kann die erste Lösung sofort abgelesen werden: $x_1=0$ ist eine Lösung, da $a \cdot 0^2+b \cdot 0=0$ unabhängig von $a$ und $b$. Die fehlende Lösung erhält man durch elementare Umformungen:

\begin{align} 0 &=a \cdot x^2+b \cdot x \ \ \ \ \text{Division durch} \ x \ \text{für} \ x \neq 0 \\ 0 &=a \cdot x +b \\ -b &=a \cdot x \\ \frac{-b}{a}& =x \end{align}

Musterbeispiel: Löse die Gleichung $0=4x^2+6x$ durch elementare Umformungen.

Lösung: Zuerst heben wir $x$ heraus: $$0=x \cdot (4x+6)$$ Hier sieht man sofort, dass $x_1=0$ eine Lösung ist, da $0 \cdot (0+6)=0$ ist. Eine Division der Gleichung durch $x$ ergibt für alle $x \neq 0$

\begin{align} 0 &=4x+6 \\ -6 &=4x \\ -\frac{3}{2}&=x \end{align}

Antwort: Die Lösungsmenge lautet somit $\mathbb{L}= \left\{-\frac{3}{2}, 0 \right\}$.

Anmerkung: Die Gleichung kann natürlich auch mit der kleinen bzw. der großen Lösungsformel gelöst werden. Dabei ist ein Parameter ($q$ bzw. $c$) null. Probiere die Lösungsformeln aus und überprüfe deine Resultate!

Anmerkung: Quadratische Gleichungen dieses Typs ($b \neq 0, \ c=0$) haben stets zwei reelle Lösungen: $\ \mathbb{L}=\left\{0, \frac{-b}{a} \right\}$

Sonderfall: $0=a\cdot x^2+c$

Für diesen Fall erfolgt die Lösung direkt durch einfache Umformungsschritte:

\begin{align} 0 &=a \cdot x^2+c \\ -c &=a \cdot x^2 \\ \frac{-c}{a} &= x^2 \\ \pm \sqrt[2]{\frac{-c}{a} }&=x_{1,2}\\ x_1=\sqrt[2]{\frac{-c}{a} } \textrm{ und }& x_2=-\sqrt[2]{\frac{-c}{a} } \end{align}

Musterbeispiel: Löse die Gleichungen $0=4x^2-6$ und $0=4x^2+6$ durch elementare Umformungen.

Lösung: Gleichung 1:

\begin{align} 6 &=4x^2 \\ \frac{6}{4} &=x^2 \\ x &= \pm \sqrt{\frac{3}{2} } \end{align}

Antwort: Die Lösungsmenge lautet somit $\mathbb{L}= \left\{-\sqrt{\frac{3}{2} }, \sqrt{\frac{3}{2} }\right\}$.

Lösung: Gleichung 2:

\begin{align} -6 &=4x^2 \\ \frac{-6}{4} &=x^2 \\ x &= \pm \sqrt{\frac{-3}{2} } \ \ \end{align} Die Wurzel einer negativen Zahl ist nicht definiert. Es gibt somit keine reelle Lösung.

Antwort: Die Lösungsmenge ist somit $\mathbb{L}= \left\{ \right\}$.

Anmerkung: Die Gleichung kann natürlich auch mit der kleinen bzw. der großen Lösungsformel gelöst werden. Dabei ist ein Parameter ($q$ bzw. $c$) null. Probiere die Lösungsformeln aus und überprüfe deine Resultate!

Anmerkung: Quadratische Gleichungen dieses Typs ($b = 0, \ c \neq 0$) haben entweder genau zwei reelle Lösungen oder keine reelle Lösung (siehe hierzu komplexe Zahlen). Genau zwei reelle Lösungen existieren, wenn der Wert unter der Wurzel $\frac{-c}{a}$ größer als Null ist. Dann ist $\ \mathbb{L}=\left\{-\sqrt[2]{\frac{-c}{a} };\sqrt[2]{\frac{-c}{a} }\right\}$. Ist der Wert unter der Wurzel kleiner als Null, so gibt es keine reelle Lösung (d. h. $\ \mathbb{L}=\left\{\right\}$ über $\mathbb{R}$), sondern nur komplexe Lösungen.

Lösungsmöglichkeiten

Wir wissen nun, dass quadratische Gleichungen die allgemeine Form $a \cdot x^2+b \cdot x +c=0$ besitzen.

Wie kann diese Gleichung geometrisch interpretiert werden?
Das Lösen einer solchen Gleichung entspricht dem Auffinden der Nullstellen der zugehörigen quadratischen Funktionen $f(x)= a \cdot x^2+b \cdot x +c $. (Siehe auch Quadratische Funktionen)

Parabeln mit 0, 1 oder 2 Nullstellen

Die Nullstellen einer quadratischen Funktion sind die Schnittpunkte der Parabel mit der $x$-Achse.

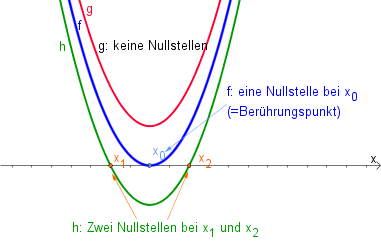
Je nachdem, wie die Parabel im Koordinatensystem liegt, gibt es:

• $2$ Nullstellen
• $1$ Nullstelle (= Scheitelpunkt liegt auf der $x$-Achse)
• $0$ Nullstellen.

Die Nullstellen einer quadratischen Funktion werden berechnet, indem man $f(x)=0$ setzt und dann die zugehörige quadratische Gleichung $$f(x)=0$$ löst.

Wie kann die Anzahl der Lösungen anhand der Lösungsformeln abgeschätzt werden?

Sowohl die große, als auch die kleine Lösungsformeln beinhalten einen Wurzelausdruck ($\sqrt{b^2-4\cdot a\cdot c}$ bei der großen Lösungsformel; $\sqrt{ {\left(\frac{p}{2} \right)}^2 -q }$ bei der kleinen Lösungsformel), der addiert bzw. subtrahiert wird, um die beiden möglichen Lösungen zu berechnen.

Für diesen Wert unter der Wurzel, die sogenannte "Diskriminante", gibt es nun drei Möglichkeiten:

• Der Wert unter der Wurzel ist größer als Null. Die Wurzel existiert somit und wird addiert bzw. subtrahiert. Es gibt also zwei Lösungen.
• Der Wert unter der Wurzel ist gleich Null. Die Wurzel existiert und es wird nichts addiert bzw. subtrahiert. Es gibt also genau eine Lösung.
• Der Wert unter der Wurzel ist kleiner als Null. Die Wurzel einer negativen Zahl hat über $\mathbb{R}$ keine Lösung. Es gibt somit keine reelle Lösung.

Anmerkung zur Theorie: Die Diskriminante

Der Wert unter der Wurzel (Radikand der Wurzel) wird bei den beiden Lösungsformeln auch als Diskriminante (von lat. discriminare = unterscheiden) bezeichnet. Der Name bezieht sich darauf, dass dieser Wert dabei hilft, die verschiedenen Lösungsfälle zu unterscheiden.