Funktionen

Funktionen

• Einleitung
• Definition einer Funktion
• Darstellung einer Funktion
• Zusammenfassendes Video
• Aufstellen einer Funktionsgleichung
• Eigenschaften von Funktionen
• Beispiele

Einleitung

Diese Seite handelt von der Definition und den grundlegenden Eigenschaften von Funktionen. Auf anderen Seiten werden wichtige Funktionstypen genauer behandelt:

• Lineare Funktionen
• Potenz- und Polynomfunktionen

  Quadratische Funktionen

  Kubische Funktionen

• Exponentialfunktionen
• Direkte und indirekte Proportionalität

$\rightarrow$ nächste Seite ...

Definition: Was ist eine Funktion und was ist keine Funktion

Definition

Eine Funktion ist eine eindeutige Zuordnung, die jedem Wert aus einer Definitionsmenge genau einen Wert aus einer Wertemenge (Zielmenge) zuordnet. Die Elemente aus der Definitionmenge $\mathbb{D}$ werden meist mit $x$ bezeichnet. Die Werte aus der Wertemenge $\mathbb{W}$ bezeichnet man mit $y$ oder $f(x)$ („$f$ von $x$“).

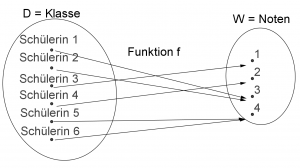
Musterbeispiel einer Funktion: Der Lehrer verteilt die Mathematiknoten

Im obigen Beispiel darf jede Schülerin nur eine Note erhalten, ABER mehrere Schülerinnen können dieselbe Note erhalten. Dies ist eine wichtige Eigenschaft von allen Funktionen. Verallgemeinert heißt dies:

Merke

Jedem Element der Definitionsmenge ($x$) darf NUR EIN Element der Wertemenge ($y$) zugeordnet werden. ABER: Ein Element der Wertemenge ($y$) kann mehreren Elementen der Definitionsmenge ($x$) zugeordnet werden. (vgl. das Musterbeispiel der Schülerinnen ($x$, Definitionsmenge) und der Noten ($y$, Wertemenge).

$\rightarrow$ nächste Seite ...

Mathematische Funktionen und ihre Darstellungen

Eine Möglichkeit eine Funktion darzustellen, ist, den Graphen der Funktion zu zeichnen.

In der Mathematik bestehen die Definitions- und Wertemenge in der Regel aus Zahlen (meist aus den reellen Zahlen.)

Somit weist die Funktion $f$ jeder Zahl $x$ einer Definitionsmenge eine andere Zahl $y$ einer Wertemenge zu.

Ein Beispiel für eine solche Zuweisung von Zahlen auf Zahlen siehst du im unteren Applet. Beachte hierbei auch die verschiedenen Darstellungen der Funktion:

a) Mengendiagramm: Die Elemente der Definitionsmenge werden durch die Funktion mit Elementen der Wertemenge verbunden.

b) Wertetabelle: In einer Tabelle werden die Zuordnungen von $x$- und $y$-Werten angegeben.

c) Graph: Die $x$- und $y$-Werte aus der Wertetabelle können in einem Koordinatensystem als Punkte mit den Koordinaten $(x\vert y)$ angegeben werden. Der Punkt $(1\vert 4)$ würde dann bedeuten, dass der Zahl $1$ aus der Definitionsmenge die Zahl $4$ in der Wertemenge zugeordnet wurde. Das entstehende Gebilde nennt man dann den Graphen der Funktion.

Darstellung: Mengendiagramm - Wertetabelle - Graph
Falls dieses Applet nicht funktioniert, klicke hier

Zuletzt gibt es noch eine weitere wichtige Darstellung einer Funktion, die

d) Funktionsgleichung
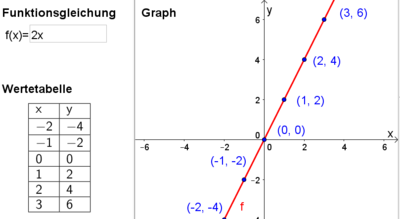
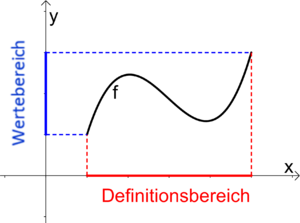
Hat man eine Funktion, die jedem Wert aus der Definitionsmenge seinen doppelten Wert zuordnet, so kann man dies auch folgendermaßen schreiben: $$f: \mathbb{D}\rightarrow \mathbb{W} \textrm{ mit } y=2x$$ wobei $x$ im Definitionsbereich und $y$ im Wertebereich liegt. Eine oft gebräuchlichere Schreibweise für eine Funktionsgleichung ist: $$f: \mathbb{D}\rightarrow \mathbb{W} \textrm{ mit } f(x)=2x$$ $$\textrm{ (gesprochen: $f$ von $x$ ist $2$ mal $x$)}$$

Beispiele für Funktionsgleichungen:

Funktionsgleichung	gesprochen	Bedeutung
$f(x)=x+1$	$f$ von $x$ ist $x$ plus $1$	Die Funktion $f$ ordnet jedem $x$ seine um $1$ höhere Zahl $x+1$ zu.
$f(x)=2x$	$f$ von $x$ ist $2$ mal $x$	Die Funktion $f$ ordnet jedem $x$ ihren doppelten Wert zu.
$f(x)=3x+1$	$f$ von $x$ ist $3$ mal $x$ plus $1$	Die Funktion $f$ ordnet jedem $x$ jene Zahl zu, die man erhält, wenn man zum Dreifachen von $x$ eins addiert.

Nun lernen wir, mithilfe einer Funktionsgleichung eine Wertetabelle und anschließend einen Graphen zu erstellen:

Gegeben ist die Funktion $f$ mit der Funktionsgleichung $f(x)=x+2$.
a) Erstelle mithilfe der Funktionsgleichung eine Wertetabelle im Definitionsbereich $[0;3]$.
b) Skizziere den Graphen der Funktion.

a) Erstelle mithilfe der Funktionsgleichung eine Wertetabelle im Definitionsbereich $[0;3]$.

Gegeben ist die Funktionsgleichung $f(\color{red}{x})=\color{red}{x}+2$ (wir könnten auch $y=x+2$ schreiben, da $f(x)=y$ ist).

Wertetabelle der Funktion $f(x)=x+2$

Um die Wertetabelle zu erstellen, setzen wir nun Zahlen aus dem Definitionsbereich $[0;3]$ für $x$ ein und berechnen damit $y$ (oder $f(x)$).

• Wenn $x=0$ dann ist: $f(\color{red}{0})=\color{red}{0}+2=2$ d. h. für $x=0$ ist $y=2$ (oder $f(\color{red}{0})=2$)
• Wenn $x=1$ dann ist: $f(\color{red}{1})=\color{red}{1}+2=3$ d. h. für $x=1$ ist $y=2$ (oder $f(1)=3$)
• Wenn $x=2$ dann ist: $f(\color{red}{2})=\color{red}{2}+2=4$ d. h. für $x=2$ ist $y=4$ (oder $f(2)=4$)
• Wenn $x=3$ dann ist: $f(\color{red}{3})=\color{red}{3}+2=5$ d. h. für $x=3$ ist $y=5$ (oder $f(3)=5$)

Natürlich können wir auch Dezimalzahlen einsetzen:

• Wenn $x=0.5$ dann ist: $f(0.5)=0.5+2=2.5$ d. h. für $x=2.5$ ist $y=2.5$ (oder $f(1.5)=2.5$)

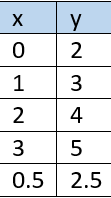
Fassen wir $x$-Werte und $y$-Werte in einer Tabelle zusammen, so erhalten wir die rechts abgebildete Wertetabelle.

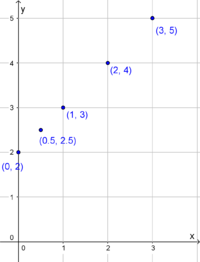
b) Skizziere den Graphen der Funktion $f$. Um den Graphen zu zeichnen, verwenden wir die Werte aus der Wertetabelle. Jede Spalte entspricht dabei einem Punkt mit $x$-Koordinate und $y$-Koordinate. Nehmen wir beispielsweise den Punkt aus der untersten Zeile $(0.5\vert 2.5)$, so müssen wir $0.5$ entlang der $x$-Achse nach rechts und $2.5$ entlang der $y$-Achse hinauf (bei Schwierigkeiten mit dem Einzeichnen der Punkte, siehe Koordinatensystem).

Zeichnest du alle Punkte ein, so erhältst du:

Einzeichnen der Punkte aus der Wertetabelle

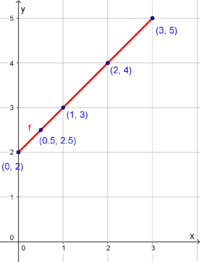
Was wir zum jetzigen Zeitpunkt noch nicht wissen ist, dass $f(x)=x+2$ eine lineare Funktion ist, dessen Graph immer eine Gerade ist. Somit können wir die Punkte verbinden und erhalten den Graphen der Funktion im Definitionsbereich $[0;3]$:

Graph der Funktion $f(x)=x+2$ im Definitionsbereich $[0;3]$

Merke

$\ $ Eine Wertetabelle erstellt man, indem man für $x$ einen Wert aus dem Definitionsbereich einsetzt und den $y$-Wert ausrechnet. Einen Graphen erstellt man, indem man zuerst die Punkte $(x\vert y)$ aus der Wertetabelle einzeichnet und anschließend passend verbindet. Den $x$-Wert nach rechts/links und den $y$-Wert hinauf/hinunter. (Beachte: Was es heißt, die Punkte „passend zu verbinden“ kommt immer auf die Art der Funktion an - dies lernst du in den weiteren Kapiteln)

Übung zur Darstellung von Funktionen: Funktionsgleichung - Wertetabelle - Graph
Löse die Aufgaben, indem du die passende Funktionsgleichung eintippst die Wertetabelle richtig stellst (rote Werte) die Punkte im Graphen an die richtige Stelle schiebst. Klicke am Ende jeder Aufgabe auf „Überprüfung“ um zu sehen, ob du die Aufgabe richtig gelöst hast.
Falls dieses Applet nicht funktioniert, klicke hier

Hinweis!

$\ $

1. Anstelle von $f$ können auch andere Buchstaben für eine Funktion verwendet werden, z. B. $g(x)=x+1$.
2. Auch muss nicht immer $x$ als Variable verwendet werden. So wird für die Zeit als Definitionsbereich meist der Buchstabe $t$ verwendet, z. B. $g(t)=t+1$.

Merke

Folgende Darstellungsformen sind in der Mathematik von großer Bedeutung: Funktionsgleichung Wertetabelle Graph einer Funktion Viele Aufgaben werden darin bestehen, zwischen diesen Darstellungsformen zu wechseln.

$\rightarrow$ nächste Seite ...

Zusammenfassendes Video

$\rightarrow$ nächste Seite ...

Aufstellen einer Funktionsgleichung - Abhängige und unabhängige Variable

Oft besteht die Aufgabe darin, aus einem Text eine passende Funktionsgleichung aufzustellen. Dabei muss zuerst überlegt werden, was die $x$- und was die $y$-Variable (oder $f(x)$) sein soll. Dabei gilt folgende Grundregel:

Merke

$\\ $ $x$ ist die unabhängige Variable $y$ oder $f(x)$ ist die von $x$ abhängige Variable

Sandra hat doppelt so viel auf ihrem Konto wie Peter. Bestimme jene Funktionsgleichung, die das Gehalt von Peter in Abhängigkeit vom Gehalt von Sandra angibt.

Peters Kontostand ist hier abhängig von Sandras. Somit ist Sandras Kontotand die unabhängige Variable $x$ und Peters Kontostand die abhängige Variable $y$:

$x$ ... Kontostand von Sandra

$y$ ... Kontostand von Peter

Da Sandra doppelt so viel wie Peter auf dem Konto hat, muss Peters Gehalt verdoppelt werden, damit beide gleich viel haben. Das bedeutet: $$2\cdot y=x$$ Formt man nun so um, sodass $y$ frei steht, erhält man: $$y=\frac{x}{2} $$ oder $$f(x) =\frac{x}{2} $$

Eine rechnerische Bestimmung der Funktionsgleichung lernst du in diesem Kapitel.

$\rightarrow$ nächste Seite ...

Eigenschaften von Funktionen

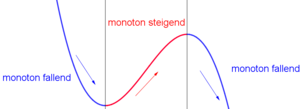
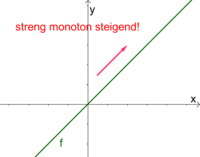
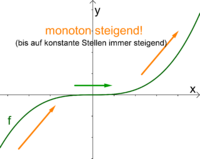
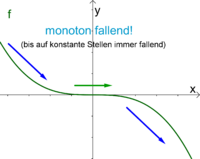
Monotonieverhalten

Das Monotonieverhalten gibt an, in welchem Bereich der Graph von links nach rechts steigt oder fällt.

Das Monotonieverhalten eines Funktion gibt an, ob der Graph steigt oder fällt, wobei immer von links nach rechts geschaut wird.

Eigenschaft	Erklärung	formale Definition	Graphik
streng monoton steigend	der Graph geht immer bergauf	Ist $x_1<x_2$, dann gilt $f(x_1)<f(x_2)$
monoton steigend	der Graph geht bis auf einzelne konstante Stellen immer bergauf	Ist $x_1<x_2$, dann gilt $f(x_1)\leq f(x_2)$
konstant	der Graph ist parallel zur x-Achse	Ist $x_1<x_2$, dann gilt $f(x_1)=f(x_2)$
monoton fallend	der Graph geht bis auf einzelne konstante Stellen immer bergab	Ist $x_1<x_2$, dann gilt $f(x_1)\geq f(x_2)$
streng monoton fallend	der Graph geht immer bergab	Ist $x_1<x_2$, dann gilt $f(x_1)>f(x_2)$

Nullstellen

Im Graphen sind die drei Nullstellen $x_1, \ x_2$ und $x_3$ abgebildet.

Definition

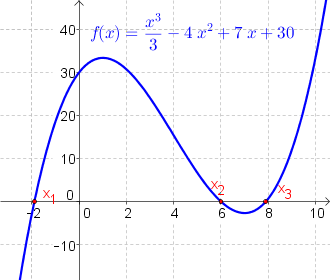
Nullstellen sind jene Stellen ($=x$-Werte), an denen der Graph der Funktion die $x$-Achse schneidet (hier ist $f(x)=0$). Formale Definition: Die Funktion $f(x)$ hat bei $x_1$ eine Nullstelle, wenn gilt: $f(x_1)=0$

Video

Wichtig: Das folgende Video ist für das jetzige Stoffgebiet nur bis zur Minute 2:00 relevant. Die anschließenden Rechenschritte lernst du erst später.

$\rightarrow$ nächste Seite ...

Interaktive Übungen

Quiz: Zusammenhänge als Funktionen erkennen (FA 1.1)

Quiz: Formeln als Funktionen (FA 1.2 + 1.8)

Quiz: Funktionen - Wechsel zwischen Darstellungsformen (FA 1.3)

Quiz: Funktionen - Ermitteln und deuten von Werten (FA 1.4)

Quiz: Funktionen - Eigenschaften (FA 1.5)

Quiz: Funktionstypen und deren Eigenschaften (FA 1.9)

Matura-Aufgaben

$Bifie$ Regenrinne (mittel-schwer-leicht)

Welche Inhalte werden hier noch gefragt: Rechnen mit Termen.

$Bifie$ Elektrischer Widerstand (leicht)

Welche Inhalte werden hier noch gefragt: Rechnen mit Termen.

$Bifie$ Torten (mittel-leicht-leicht-leicht)

Welche Inhalte werden hier noch gefragt: Gleichungssysteme sowie Formeln und für d) Binomialverteilung (erst in der 5. Klasse)

$Bifie$ Beleuchtungsstärke

Weitere Übungen und Ausblick

• $Aha!$ Überblicksblatt samt Beispielen - was du zur Matura alles über Funktionen wissen musst

• ? : Übung, in der du lernst, Funktionsgleichungen anhand gegebener Punkte zu berechnen

Hierfür musst du Gleichungssysteme lösen.

$\rightarrow$ nächste Seite ...