Zahlenmengen
Inhaltsverzeichnis
Was unterscheidet $2, -8, 3.5$ oder $\sqrt{7}$?
Es sind alles Zahlen, allerdings sind sie unterschiedlich:
- Einerseits ist ihr Wert unterschiedlich ($2 ≠ -8 ≠ 3.5 ≠ \sqrt{7}$).
- Andererseits gehören die Zahlen unterschiedlichen Zahlenmengen an.
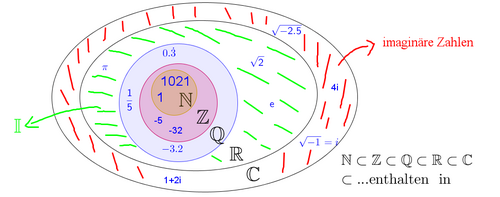
Folgenden Zahlenmengen wirst du in der Schule und im Studium begegnen:
Die natürlichen Zahlen $\mathbb{N}$
|
Die natürlichen Zahlen $\mathbb{N}$ sind die Zahlenmenge $\mathbb{N}=\{0,1,2,3,...\}$. |
Sie sind "abgeschlossen" bezüglich Addition und Multiplikation. Das heißt, wenn man zwei natürliche Zahlen addiert bzw. multipliziert, so landet man wieder bei einer natürlichen Zahl.
Beispiele
- $ 7+15=22 $
- $ 7\cdot 15=105 $
Sowohl die beiden Summanden bzw. Faktoren auf der linken Seite als auch die Summe bzw. das Produkt auf der rechten Seite sind natürliche Zahlen. Es ist nicht möglich, zwei natürliche Zahlen zu addieren oder zu multiplizieren und dabei eine "nicht-natürliche" Zahl zu erhalten.
Die ganzen Zahlen $\mathbb{Z}$
|
Die ganzen Zahlen $\mathbb{Z}$ sind die Zahlenmenge $\mathbb{Z}=\{...,-3,-2,-1,0,1,2,3,...\}$. |
Beachte, dass jede natürliche Zahl auch eine ganze Zahl ist! Um auf die ganzen Zahlen zu kommen, fügt man den natürlichen Zahlen einfach alle negativen ganzen Zahlen hinzu.
$\mathbb{Z}$ ist "abgeschlossen" bezüglich der Addition, der Multiplikation und der Subtraktion.
Beispiele
- $-3+7=4$
- $(-2) \cdot 3=-6$
- $ -8-17=-25$
Was ist nun aber, wenn man zwei ganze Zahlen dividiert?
Beispiel: $$-2:4= \frac{-2}{4}=-\frac{1}{2}$$
Die Zahl$ -\frac{1}{2}$ ist ein Bruch und sicherlich keine ganze Zahl mehr. Hier sind wir in der nächsten Zahlenmenge gelandet.
Deshalb fügt man nun zu den ganzen Zahlen alle Brüche hinzu und erhält:
Die rationalen Zahlen $\mathbb{Q} $
|
Zu den rationalen Zahlen gehören alle Brüche mit Zähler und Nenner aus den ganzen Zahlen, wobei im Nenner natürlich keine $0$ stehen darf. Formal kann man das folgendermaßen schreiben:
$$ \mathbb{Q} = \left\{ \frac{a}{b} \vert\ a,b \in \mathbb{Z}, b \neq 0\right\} $$ |
Da man jeden Bruch in eine endliche oder unendlich periodische Dezimalzahl verwandeln kann, indem man Zähler durch Nenner dividiert, gehören zu $\mathbb{Q} $ auch alle endlichen ODER unendlich periodischen Dezimalzahlen.
Beispiel: $$ \frac{1}{3}=0.333333...$$ oder $$ \frac{1}{5}=1:5=0.2 $$
Nun gibt es aber noch Dezimalzahlen, die unendlich lang, aber niemals periodisch sind. Diese liegen außerhalb von $\mathbb{Q} $ und heißen irrationalen Zahlen $\mathbb{I}$.
Die irrationalen Zahlen $\mathbb{I}$
|
Zu den irrationalen Zahlen $\mathbb{I}$ gehören alle Dezimalzahlen, die unendlich lang UND niemals periodisch sind. |
Beispiele:
- $0,1001000100001...$ (immer eine $0$ mehr)
- $\pi =3.14159... $
- $e =2.718...$ (die eulersche Zahl)
- $\sqrt{2}=1.414...$ (und alle weiteren Wurzeln von Primzahlen).
Die reellen Zahlen $\mathbb{R}$
Fasst man nun alle Dezimalzahlen zusammen, die
- endlichen oder unendlich periodischen ($=$ rationale Zahlen) und die
- unendlichen aber niemals periodischen (irrationale Zahlen)
so erhält man die reellen Zahlen $\mathbb{R}$.
|
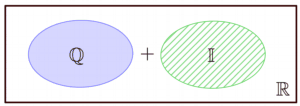
$$ \mathbb{R} = \mathbb{Q} \cup \mathbb{I} $$
Vereinfacht gesagt: $ \mathbb{R}= $ Menge aller Dezimalzahlen |
In den reellen Zahlen $\mathbb{R}$ kann addiert, subtrahiert, multipliziert, dividiert und die Wurzeln positiver Zahlen berechnet werden.
Die imaginären Zahlen
Während in den reellen Zahlen $\mathbb{R}$ addiert, subtrahiert, multipliziert und dividiert werden kann, kann man aber die Wurzel aus negativen Zahlen NICHT berechnen.
Beispiel:
$ \sqrt{-1} \notin \mathbb{R} $
Aus diesem Grund erweitert man die reellen Zahlen mit allen negativen Wurzeln und nennt sie
|
die imaginären Zahlen $=$ die Menge der negativen Wurzeln $= \left\{ \sqrt{-b}\ \vert\ b\in \mathbb{R}^+\right\}$. |
Weitere Beispiele:
- $ \sqrt{-1}=i$
- $ \sqrt{-4}=2i\ \ $ (weil $\sqrt{4\cdot (-1)}= \sqrt{4}\cdot \sqrt{-1}=2\cdot i $)
Imaginäre Zahlen treten u. a. bei den quadratischen Gleichungen auf, wenn die entsprechende Parabel keine Nullstelle hat.
Die komplexen Zahlen $\mathbb{C}$
Die komplexen Zahlen $\mathbb{C}$ erhält man, wenn man die reellen Zahlen $\mathbb{R}$ und die imaginären Zahlen zusammenfügt.
|
$$ \mathbb{C} = \mathbb{R} \cup \textrm{imaginäre Zahlen}$$ |
Setzt man also eine reelle Zahl (z. B. $5$) und eine imaginäre Zahl (z. B. $7i$) zusammen, so erhält man die komplexe Zahl $$5+7i$$
Beispiele
- $2$ + $3$ $i$
(Jede komplexe Zahl besteht aus einer reellen Zahl, dem sogenannten Realteil (hier: $2$) und einer imaginären Zahl (hier $3i$), wobei $3$ der sogenannte Imaginärteil ist.
- $-9+18i$ (Realteil $=-9$ und Imaginärteil $=18$)
- $4$ $\ \ $ (hier ist der Imaginärteil $0$)
- $8i$ $\ \ $(hier ist der Realteil $0$)
Quiz: Zahlenmengen (AG 1.1)