Lineare Funktionen
Inhaltsverzeichnis
| Infobox: Lineare Funktionen | |
|---|---|
| Inhaltsbereich: Funktionale Abhängigkeiten (FA) | |
|
Semester:
| |
| Vorwissen: Funktionen | |
| Folgethemen: Gleichungssysteme; Quadratische Funktionen | |
Unterrichtsideen:
| |
|
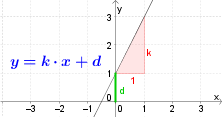
Die Funktionsgleichung einer linearen Funktion lautet $$ y=k\cdot x+d$$
mit $k,d\in$ $\mathbb{R} $. |
|
Der Graph einer linearen Funktion ist IMMER eine Gerade. |
Graph einer linearen Funktion
Der Graph einer linearen Funktion ist immer eine Gerade. Verändere im folgenden Applet die Werte von $k$ und $d$ und beobachte, was passiert.
Sollte die folgende Animation nicht funktionieren, klicke auf diesen Link .
Steigung $k$
Der Parameter $k$ gibt die (prozentuelle) Steigung der Geraden an. Die Steigung $k$ kann graphisch aus einer Zeichnung oder rechnerisch bestimmt werden.
Steigungsdreieck
Wenn man von einem beliebigen Punkt auf der Geraden $1$ nach rechts und anschließend hinauf bzw. hinab zeichnet, um wieder auf der Geraden zu landen, erhält man ein rechtwinkliges Dreieck. Man nennt es Steigungsdreieck. Der Höhenunterschied des Dreiecks entspricht dann der Steigung $k$.
|
„Fällt“ der Graph einer linearen Funktion, so ist $k$ negativ. „Steigt“ der Graph einer linearen Funktion, so ist $k$ positiv. |
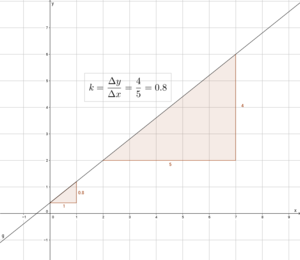
Oft wäre diese Vorgehensweise zu ungenau. Man kann deshalb auch größere Steigungsdreiecke einzeichnen. Dann muss man jedoch die Länge der senkrechten Kathete durch die Länge der waagrechten Kathete dividieren und es gilt:
$$k=\frac{Höhenunterschied}{Längenunterschied}=\frac{\Delta y}{\Delta x}$$
$\Delta y$ ... Länge der senkrechten Kathete (inkl. Vorzeichen!)
$\Delta x$ ... Länge der waagrechten Kathete
Steigung aus Zahlenpaaren
Wenn man von einer linearen Funktion zwei Zahlenpaare $(x|f(x))=(x|y)$ kennt oder aus einem Graph abgelesen oder berechnet hat, kann man ihre Steigung $k$ einfach bestimmen:
Aus den Punkten $P(x_1|y_1)$ und $Q(x_2|y_2)$ erhält man die Steigung $k$ durch $$k=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1} $$ (siehe Differenzenquotient)
|
Die Reihenfolge der Punkte ist egal. Die Koordinaten der Punkte müssen aber zusammenpassen. Also „erster Punkt minus zweiter Punkt“ oder „zweiter Punkt minus erster Punkt“. |
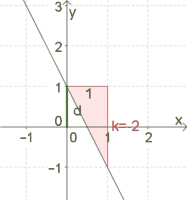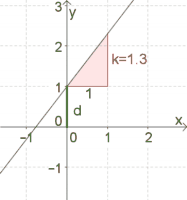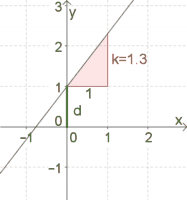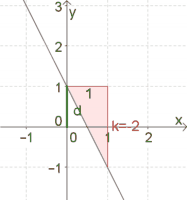
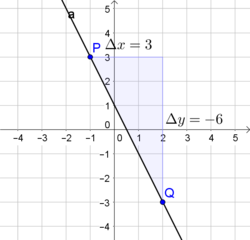
Ermittle die Steigung der Geraden, auf der die Punkte $P(-1\vert 3)$ und $Q(2\vert -3)$ liegen.
Möglichkeit 1: Zeichne die zwei Punkte $P$ und $Q$ in ein Koordinatensystem und zeichne die verbindende Gerade ein.
Durch Einzeichnen des Steigungsdreiecks zwischen $P$ und $Q$ können auch $\Delta x$ und $\Delta y$ leicht abgelesen werden (siehe Abb.).
Es folgt daraus $k=\frac{\Delta y}{\Delta x}=\frac{-6}{3}=-2$
Möglichkeit 2: Nachdem die Gerade eingezeichnet wurde, kann ein Steigungsdreieck der Breite $1$ eingezeichnet werden, aus dem $k=-2$ sofort abgelesen werden kann.
Möglichkeit 3: Direkte rechnerische Bestimmung mittels Differenzenquotient:
$k=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}=\frac{-3-3}{2-(-1) }=\frac{-6}{3}=-2$
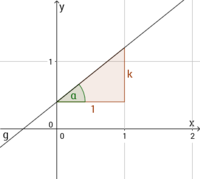
Steigungswinkel
Manchmal ist der Steigungswinkel einer linearen Funktion gegeben oder gesucht. Das Steigungsdreieck führt zum Zusammenhang zwischen der Steigung $k$ und Steigungswinkel $\alpha$. Aus $\tan(\alpha)=\frac{GK}{AK}$ folgt $$k=\tan(\alpha)$$ (siehe Trigonometrie)
Abstand $d$ auf der $y$-Achse („Ordinatenabschnitt“)
$d$ gibt den $y$-Wert des Schnittpunkts der Geraden mit der $y$-Achse an.
$d$ kann aus dem Graph abgelesen werden (manchmal nur ungenau) oder berechnet werden, indem man $x=0$ setzt.
Eigenschaften:
- ist $d=0$, so geht die Gerade durch den Ursprung. Solche Funktionen nennt man homogene lineare Funktionen. Ist $d\neq 0$, so nennt man die Funktion inhomogen.
- bei Kostenfunktionen gibt $d$ die Fixkosten an.
Berechnung von $d$
Wenn $d$ noch nicht bekannt ist, kann es aus zwei Punkten, die auf der Geraden liegen, berechnet werden. Diese Punkte sind entweder bekannt oder können aus dem Graph abgelesen werden.
1. Schritt: Berechnung von $k$ (siehe oben)
2. Schritt: $k$ und einen der beiden Punkte in \(y=k\cdot x+d\) einsetzen. $d$ sollte dann die einzige Unbekannte in einer linearen Gleichung sein. Durch Lösen der Gleichung erhält man $d$.
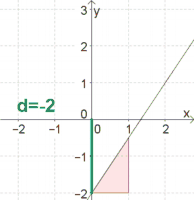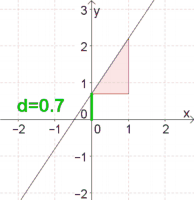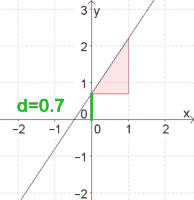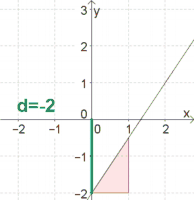
Ermittle $d$ jener Geraden, auf der die Punkte $P(-1\vert 3)$ und $Q(2 \vert -3)$ liegen.
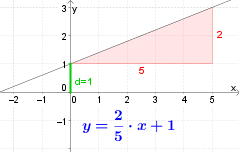
Möglichkeit 1: Zeichne die zwei Punkte $P$ und $Q$ in ein Koordinatensystem und zeichne die verbindende Gerade ein.
Man sieht, dass die Gerade die $y$-Achse bei $1$ schneidet. $d$ ist also $1$.
Möglichkeit 2: Direkte rechnerische Bestimmung mittels Gleichung:
$3=-2 \cdot (-1)+d \Leftrightarrow 3=2+d \Leftrightarrow 1=d$
Graph zeichnen (Gerade)
Der Graph einer linearen Funktion ist eine Gerade. Man kann sie entweder mithilfe zweier Zahlenpaare (Wertetabelle) oder $k$ und $d$ zeichnen.
Zahlenpaare
Zeichne zwei Zahlenpaare als Punkte in ein Koordinatensystem und lege eine Gerade durch sie. Wenn du noch keine Zahlenpaare hast, kannst du sie aus der Wertetabelle der Funktion nehmen bzw. $x$-Werte in die Funktionsgleichung einsetzen. Achte darauf, dass die Punkte weit voneinander entfernt liegen, dann wird die Zeichnung genauer!
$k$ und $d$
- $d$ hinauf/hinab
- eins nach rechts
- $k$ hinauf/hinab
Ist $k$ ein Bruch, d. h. $k=\frac{Zähler}{Nenner}$, dann kannst du
- $d$ hinauf/hinab
- Nenner nach rechts
- Zähler hinauf/hinab
Gerade mit gegebener Funktionsgleichung zeichnen
| Falls das Applet nicht funktioniert, klicke hier |
Besondere Eigenschaften (inkl. direkter Proportionalität)
Lineare Funktionen erfüllen die Eigenschaft $f(x+1)=f(x)+k$
Beweis: $f(x+1)=k\dot (x+1)+d=kx+k+d=kx+d+k=f(x)+k$
Außerdem ist die Ableitung der linearen Funktion gleich $k$: $\frac {f(x_2)-f(x_1)} {x_2-x_1}=k=f´(x)$
Lineare Funktionen der Form $f(x)=k \cdot x$ werden auch als direkte Proportionalitätsfunktionen bezeichnet. Diese gehen stets durch den Ursprung. Direkte Proportionalitätsfunktionen haben die besondere Eigenschaft, dass wenn x mit einem bestimmten Faktor multipliziert wird, sich auch f(x)um denselben Faktor verändert. Z.B. x wird verdoppelt, so verdoppelt sich auch f(x). Weitere Informationen findest du im Abschnitt Direkte Proportionalität
Video
Was nicht fehlen darf - ein Lied von DorFuchs: (Anmerkung: In Deutschland werden anstatt $k$ und $d$ die Variablen $m$ und $n$ verwendet.)
Lernpfad: Bedeutung von k und d
Anwendungen
In folgenden Kapiteln kommen lineare Funktionen wieder vor:
- Lineare Kosten (siehe Beispiele)
- Wachstums- und Zerfallsprozesse
- Kurvendiskussionen
Inhaltsverzeichnis
Quiz: Lineare Funktionen (FA 2.1-2.6)
Bestimmen der Funktionsgleichung
Im folgenden Applet kannst du dein Wissen testen. Gib dazu die Gleichung der Funktionsgleichung in das Eingabefeld ein. Beachte, dass Kommazeichen durch Punkte angegeben werden (z. B. $0.75$).
| Falls das Applet nicht funktioniert, klicke hier |
Bifie-Aufgaben
- $Bifie$: Kleintransporter
- Siehe auch: Gleichungssysteme
- $Bifie$: Planetenbahnen (leicht-mittel-leicht)
- Siehe auch: Gleitkommazahlen
- $Bifie$: Kleidungs- und Schuhproduktion (Bifie-Aufgabe: mittel-mittel-leicht-mittel)
- Welche Inhalte werden hier noch gefragt: Für c) und d) Prozentrechnung (1.5.)
- $Bifie$: Hochbeet (Bifie-Aufgabe: leicht-mittel-mittel)
- Welche Inhalte werden hier noch gefragt: Formeln
- $Bifie$: Impfstoff
- Welche Inhalte werden hier noch gefragt: Gleichungssysteme
Schularbeiten- und Testaufgaben
1. Aufgabe: Gib zwei Geradengleichungen in der Form $y=kx+d$ an, bei denen die entsprechenden Geraden parallel zueinander sind. Wie erkennt man bei den Gleichungen auf einen Blick, dass die Geraden parallel sind?
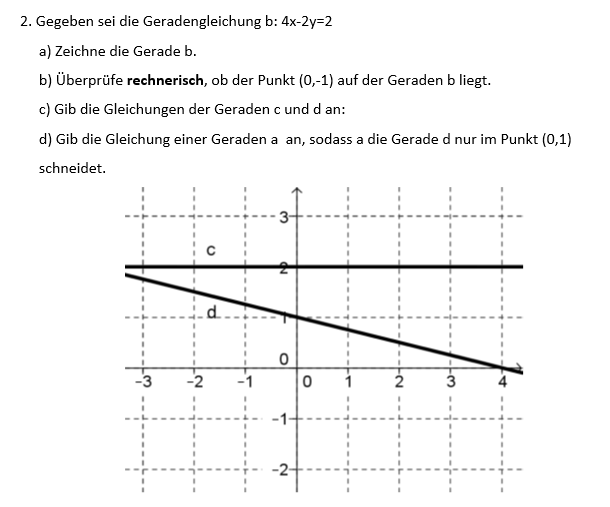
2. Aufgabe:
3. Aufgabe:
4. Aufgabe: Die Gerade der Form $y=kx+d$ geht durch die Punkte $(1,1)$ und $(4,3)$. Ermittle $k$ und $d$.
5. Aufgabe: Die Kommunikationsfirma P-Mobile plant einen Handytarif mit $5 €$ Grundgebühren. Aus wirtschaftlichen Gründen will sie, dass ein Kunde bei $500$ verbrauchten Gesprächsminuten eine Rechnung von insgesamt $20 €$ zahlen muss.
Ermittle die Kosten für eine Gesprächsminute. Bestimme die lineare Kostenfunktion des Tarifs.
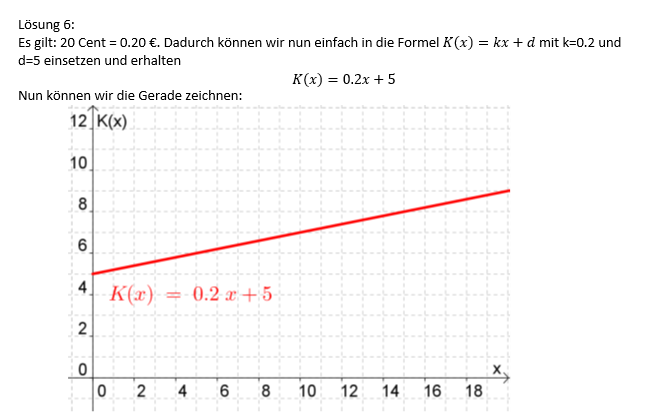
6. Aufgabe: Die Grundgebühr eines Handytarifs beträgt $5 €$. Für jede Gesprächsminute werden zusätzlich $20$ Cent verrechnet. Stelle die Gesamtkosten in Abhängigkeit von den Gesprächsminuten in einem passenden Koordinatensystem graphisch dar.
Online-Materialien
- $Schau!$ : Hier findest du eine Prezi-Überblickpräsentation (erstellt von Raimund Porod)
- $Step\ by\ Step!$ : Hier findest du einen Online-Lehrpfad zu den linearen Funktionen
Online-Übungen
- ? : Selbsttest zum Thema Geradengleichung bestimmen
- ? : Übung zur Bestimmung der Funktionsgleichung
- ? : Weitere Aufgaben zum Bestimmen der Funktionsgleichung