Gleichungssysteme

Gleichungssysteme

Definition

Ein lineares Gleichungssystem besteht aus mehreren linearen Gleichungen mit mehreren Variablen. Beispiel für ein Gleichungssystem mit $2$ Gleichungen und $2$ Variablen: $$ I: x+y=35 $$ $$ II: 2x+4y=94 $$

Gleichungssysteme mit $2$ Variablen

Beispiel: $$ I: x+y=35 $$ $$ II: 2x+4y=94 $$ Hierbei sind $x$ und $y$ die Variablen. Um die Lösungsmenge eines Gleichungssystems mit $2$ Variablen zu berechnen, braucht es in der Regel genau $2$ linear unabhängige Gleichungen.

Lösungsmenge $\mathbb{L}$

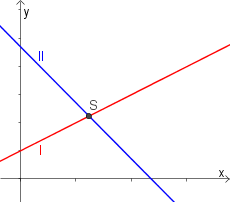
Die Lösung eines solchen Gleichungssystems ist jener Punkt $(x|y)$, der sowohl die erste Gleichung als auch die zweite Gleichung löst.

Zeige, dass der Punkt $(12\vert 23)$ das folgende Gleichungssystem löst: $ \begin{align} \ I:&\quad x&+\quad &y&=\quad &35& \textrm{ } \\ \ II:&\quad 4x&+\quad &2y&= \quad &94& \end{align}$

Begründung: Setze den Punkt $(12\vert 23)$ in die beiden Gleichungen ein, wobei $x=12$ und $y=23$ ist:

$$ I: \underbrace{12+23}_{35}=35\ \ \textrm{ wahre Aussage}$$ $$ II: \underbrace{4\cdot 12+2\cdot 23}_{\underbrace{48+46}_{94} }=94 \textrm{ wahre Aussage} $$

Somit ist $(12\vert 23)$ eine Lösung des Gleichungssystems.

Um ein Gleichungssystem zu lösen, gibt es mehrere Verfahren:

Lösungsverfahren

Additionsverfahren (Eliminationsverfahren)

Merke

Methode des Additionsverfahrens Forme beide Gleichungen auf die Form $ax+by=c$ (Variablen links, Konstante rechts). Multipliziere eine oder beide Gleichungen mit einer Zahl, sodass in beiden Gleichungen die Koeffizienten vor der Unbekannten $x$ oder vor der Unbekannten $y$ gleich sind. Addiere (oder subtrahiere) die beiden Gleichungen. Du erhältst eine Gleichung mit einer Unbekannten. Löse die Gleichung mit einer Unbekannten durch Umformen der Gleichung.

Bestimme mithilfe des Additionsverfahrens die Lösungsmenge des Gleichungssystems: $ \begin{align} \ I:&\quad x&+\quad &y &=\quad & 35& \textrm{ } \\ \ II:&\quad 4x&+\quad &2y&=\quad &94& \end{align}$

1. Schritt: Umformen auf $ax+by+c$ (hier nicht nötig):

$ \begin{align} x&+&y &=& 35& \textrm{ } \\ 4x&+&2y&=&94& \end{align}$

2. Schritt: Multipliziere eine der beiden Gleichungen:

$ \begin{align} x&+&y &=& 35& \textrm{ } \vert \cdot (-2) \\ 4x&+&2y&=&94& \end{align}$

3. Schritt: Addiere oder subtrahiere die beiden Gleichungen:

$ \begin{align} -2x&-&2y &=& -70& \textrm{ } \vert +\ \ \\ 4x&+&2y&=&94& \\ \end{align}$

4. Schritt: Lösen der Gleichung mit einer Unbekannten:

$ \begin{align} 2x&+&0&=24 & \vert :2 \end{align}$

$ \begin{align} x&=&12 \end{align}$

Nun setzen wir $x=12$ in eine der Gleichungen (z. B. in die erste) ein und erhalten: $$ \begin{align} 12+y=35 \Rightarrow y=23 \end{align}$$ Damit ist die Lösungsmenge $\mathbb{L}$ $= \{ (12\vert 23) \} $

Wichtig:

Das Additionsverfahren eignet sich nur für lineare Gleichungssysteme. Kommen nichtlineare Terme wie $x^2$, $x^3$ oder $x\cdot y$ in Gleichungen vor, so funktioniert das Additionsverfahren nicht. Um nichtlineare Gleichungssysteme zu lösen, verwendet man das Einsetzungs-, Gleichsetzungs- oder das graphische Verfahren:

Einsetzungsverfahren (Substitutionsverfahren)

Merke

Methode des Einsetzungsverfahrens 1. Stelle in einer der Gleichungen eine der Variablen frei (siehe Gleichungen umformen). 2. Setze nun das Ergebnis aus der Umformung in die andere Gleichung ein. Du erhältst eine Gleichung mit einer Variablen. 3. Löse nun diese Gleichung und setze die Lösung anschließend in die andere Gleichung ein, um die Lösung für die andere Variable zu erhalten.

Bestimme mithilfe des Einsetzungsverfahrens die Lösungsmenge des Gleichungssystems: $ \begin{align} \ I:&\quad x&+\quad &y &=\quad & 35& \textrm{ } \\ \ II:&\quad 4x&+\quad &2y&=\quad &94& \end{align}$

1. Schritt: Umformen der Gleichung I $\rightarrow$ $x$ freistellen:

$ \begin{align} I:\ \ &x+y &= &35 \ \ \ \ \ \ \ \ \vert \ -y \\ I:\ \ &x &= &35-y \end{align}$

2. Schritt: Setze das Ergebnis in die Gleichung II ein:

$ \begin{align} II:\ \ 4\color{red}{x}&+ &2y&= &94& \textrm{ }\ \ \ \ \vert I:\ \color{red}{x=(35-y)} \\ II:\ \ 4\cdot \color{red}{(35-y)}&+ &2y&= &94& \end{align}$

3. Schritt: Lösen der Gleichung II (hier befindet sich nun nur noch die Variable $y$)

$ \begin{align} II:\ 4\cdot (35-y)+2y&=94& \\ II:\ 140-4y+2y&=94 & \\ 140-2y&=94&\ \vert -140\\ -2y&=-46&\ \vert : (-2)\\ y&=23 \end{align}$

Nun setzen wir $y=23$ in die umgeformte Gleichung I (siehe Schritt 1) ein und erhalten: $$ x=35-y \Rightarrow x=35-23 \rightarrow x=12$$ Damit ist die Lösungsmenge $\mathbb{L}$ $= \{ (12\vert 23) \} $

Graphisches Verfahren

Der Schnittpunkt $S$ ist die Lösung des Gleichungssystems.

Merke

Methode: 1. Beide Gleichungen auf „$y=...$“ umformen. 2. Einzeichnen der Geraden aus I. und II. in dasselbe Koordinatensystem (siehe Lineare Funktionen $y=kx+d$). 3. Ermitteln des Schnittpunktes $\rightarrow$ dieser gibt die Lösungsmenge des Gleichungssystems an.

Bestimme mithilfe des graphischen Verfahrens die Lösungsmenge des Gleichungssystems: $ \begin{align} \ I:&\quad x&+\quad &y &=\quad &35& \\ \ II:&\quad 4x&+\quad &2y&=\quad &94& \end{align}$

1. Schritt: Beide Gleichungen auf „$y=...$“ umformen.

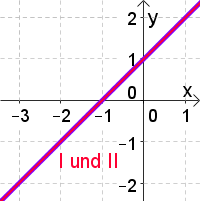
$\begin{align} I: x+y=35 &\ \ \vert -x &\rightarrow & & \rightarrow &\underline{I:y=-x+35} \\ \\ II:4x+2y=94 &\ \ \vert -4x &\rightarrow &2y=-4x+94 \ \ \vert :2 & \rightarrow &\underline{II:y=-2x+47} \end{align}$

2. Schritt: Einzeichnen der Geraden $y=kx+d$ (siehe Geraden zeichnen)

Der Schnittpunkt der Geraden $I:y=-x+35$ (rot) und $II:y=-2x+47$ (blau) ist $S(12\vert 23)$

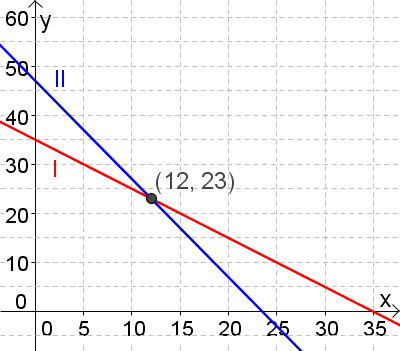
3. Schritt: Ermitteln des Schnittpunktes.

Wie man aus der obigen Graphik erkennt, hat der Schnittpunkt die Koordinaten $S(12\vert 23)$. Somit lautet die Lösungsmenge $\mathbb{L}$$={(12\vert 23)}$.

Achtung: Oft ist es schwer, den Schnittpunkt durch eine händische Zeichnung exakt zu ermitteln. Hier ist es dann oft sinnvoll, Technologie einzusetzen. Entweder mithilfe

• von GeoGebra oder
• des Intersect-Befehls des TI.

Matrixverfahren (nur mit dem TR Ti-82)

siehe Matrixverfahren mit dem TR

Verfahren mit GeoGebra-CAS

folgt in Kürze ...

Lösungsmöglichkeiten eines linearen Gleichungssystems

Betrachtet man ein lineares Gleichungssystem mit $2$ Variablen graphisch, indem man die Geraden zeichnet (siehe Graphisches Verfahren), so gibt es insgesamt drei Lösungsmöglichkeiten:

1. Die Geraden schneiden sich im Schnittpunkt $S(x|y)\ \rightarrow$ es gibt eine Lösung: $\mathbb{L}={(x|y)}$
2. Die Geraden sind parallel und es gibt keinen Schnittpunkt $\rightarrow$ es gibt keine Lösung: $\mathbb{L}=\{\ \}$
3. Die Geraden überlappen sich und es gibt unendlich viele Schnittpunkte $\rightarrow$ es gibt unendlich viele Lösungen, die alle auf der Geraden liegen: $\mathbb{L}=\{ (x\vert y)\vert (x|y)\textrm{ erfüllt die Geradengleichung} \}$

Wie erkennen wir nun diese drei Fälle, wenn wir ein Lösungsverfahren verwenden? Die folgende Grafik zeigt dies genauer:

$\ $	1. Fall: genau eine Lösung	2. Fall: keine Lösung	3. Fall: unendlich viele Lösungen
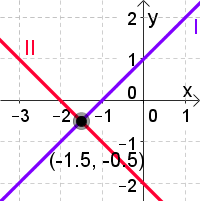
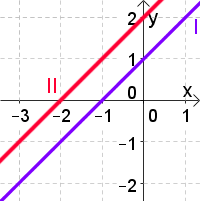
Beispiel: Die Gleichungen sind	linear unabhängig und widerspruchsfrei: $$I:-x+y=1$$ $$II:-x-y=2$$	widersprüchlich $$I:-x+y=1$$ $$II:-x+y=2$$	linear abhängig (II ist ein Vielfaches von I): $$I:-x+y=1$$ $$II:-2x+2y=2$$
Anzahl der Lösungen:	genau eine $x=-1.5$ und $y=-0.5$	keine	unendlich viele z. B. $(0|1);(1|2);(3|4)...$
Lösungsmenge	$$\mathbb{L}={(-1.5|-0.5)}$$	$$\mathbb{L}=\{\ \}$$	$$\mathbb{L}=\{ (x|y)|-x+y=1\}$$ D. h. alle Punkte $(x|y)$, die die Gleichung $-x+y=1$ erfüllen.
Graphisches Lösungsverfahren
Additions- und Einsetzungsverfahren	$x=-1.5$ und $y=-0.5$	eine falsche Aussage wie $0=1$ oder $4=18$... Somit gibt es keine Werte als Lösung.	eine wahre Aussage wie $0=0$ oder $2=2$ Somit ist jede Zahl (die eine der beiden Gleichungen erfüllt) eine Lösung.
Matrixverfahren	$1$ $0$ $-1.5$ $0$ $1$ $-0.5$	Die unterste Zeile besteht aus: $0$ $0$ $1$ Somit gilt: $0x+0y=1$ und damit $0=1$ f. A. $\rightarrow$ Es gibt keine Lösung.	Die unterste Zeile besteht aus: $0$ $0$ $0$ Somit gilt: $0x+0y=0$ und damit $0=0$ w. A. $\rightarrow$ Es gibt unendlich viele Lösungen.
Lösung mit GeoGebra-CAS	$$x = -1.5,\ y = -0.5$$	$$\textrm{ ? }$$	$$x = y - 1, y = y$$

Lineare Gleichungssysteme mit $3$ oder mehreren Variablen

Musterbeispiel: Das folgende lineare Gleichungssystem zeigt ein Gleichungssystem mit $3$ Variablen ($x, y$ und $z$) und $3$ Gleichungen:

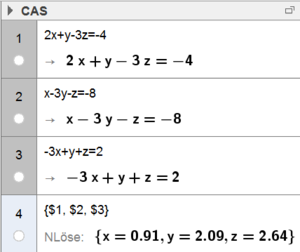
$\begin{align} I: &2x&+&y&-&3z&=&-4\\ II: &x&-&3y&-&z&=&-8\\ III: &-3x&+&y&+&z&=&\ \ 2 \end{align}$

Es gilt: Um ein lineares Gleichungssystem mit $n$ Variablen eindeutig zu lösen, muss das Gleichungssystem aus $n$ linear unabhängigen Gleichungen bestehen.

Bestimme die Lösungsmenge des folgenden Gleichungssystems: $\begin{align} I: &2x&+&y&-&3z&=&-4\\ II: &x&-&3y&-&z&=&-8\\ III: &-3x&+&y&+&z&=&\ \ 2 \end{align}$

Mithilfe von Technologie-Einsatz kann dieses Gleichungssystem einfach gelöst werden:

GeoGebra-CAS	Matrixverfahren
Durch Markieren der $3$ Gleichungen und Klicken auf $[x=]$ ($x$-Löse) erhält man die Lösung des Gleichungssystems.	Zuerst tippt man bei [Matrix]->Edit die Koeffizienten ein: $2$ $1$ $-3$ $-4$ $1$ $-3$ $-1$ $-8$ $-3$ $1$ $1$ $2$ Dann wendet man den Befehl $rref(A)$ und erhält: $1$ $0$ $0$ $0.91$ $0$ $1$ $0$ $2.09$ $0$ $0$ $1$ $2.64$ Somit gilt: $x=0.91,\ y=2.09\ z=2.64$

Matura-Aufgaben

• $Bifie$ Wanderweg

  Siehe auch: Bewegungsaufgaben - Weg/Geschwindigkeit/Beschleunigung und Lineare Funktionen

• $Bifie$ Kleintransporter

  Siehe auch: Lineare Funktionen

• $Bifie$ Impfstoff

  Welche Inhalte werden hier noch gefragt: Lineare Funktionen

• $Bifie$ Torten (Bifie-Aufgabe: mittel-leicht-leicht-leicht)

  Welche Inhalte werden hier noch gefragt: Formeln sowie Funktionen und für d) Binomialverteilung