Wahrscheinlichkeit: Diskrete Zufallsvariablen und die Binomialverteilung

Zufallsvariablen
Diskrete Zufallsvariablen
Bernoulli-Experimente und die Binomialverteilung
Übungs- und Maturaaufgaben

Zufallsvariablen

Definition

Das Ergebnis eines Zufallsexperimentes kann mithilfe einer „Zufallsvariable“ $X$ beschrieben werden.

Die Zufallsvariable ordnet dabei jedem Einzelereignis eine reelle Zahl zu.

Beispiel: Beim Würfeln mit einem Würfel kann die Zufallsvariable die Werte $1, 2, 3, 4, 5$ oder $6$ zufällig annehmen (d. h. $X\in \{1;2;3;4;5;6\}=$ Wertebereich von $X$). Die Wahrscheinlichkeit, dass $X$ die Zahl $6$ annimmt ist: $$P(X=6)=P(6er\ \text{würfeln})=\frac{1}{6}$$

Man unterscheidet $2$ Typen von Zufallsvariablen:

Die diskrete Zufallsvariable hat einen abzählbaren Wertebereich (z. B. Anzahl von Personen).
Die stetige Zufallsvariable hat als Wertebereich ein Intervall in den reellen Zahlen und damit einen nicht abzählbaren Wertebereich.

Mithilfe der Zufallsvariable wird uns nun das Berechnen der folgenden Aufgaben erleichtert.

Inhaltsverzeichnis

1 Diskrete Zufallsvariablen

Diskrete Zufallsvariablen

Diskrete Zufallsvariablen haben einen abzählbaren Wertebereich (z. B. Anzahl von Personen).

Wahrscheinlichkeits- und Verteilungsfunktion

Definition

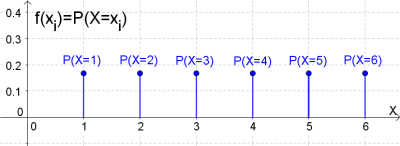
Die Wahrscheinlichkeitsfunktion $f$ ordnet jedem Einzelereignis seine Wahrscheinlichkeit zu:

$$f: f(x_i)=P(X=x_i)$$ wobei $x_i$ ein Einzelereignis (z. B.: $x_1...1er\ \text{würfeln},\ x_2...2er \text{würfeln}$ usw.) und $P(X=x_i)$ die dazugehörige Wahrscheinlichkeit ist: $P(X=x_1)=P(X=1er)=\frac{1}{6}...$)

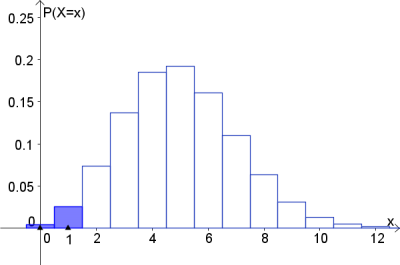
Die folgende Abbildung zeigt die Wahrscheinlichkeitsfunktion für die Zufallsvariable $X$, die die Augenzahl beim zufälligen Wurf eines Würfels zählt:

Jedes Ereignis $x_i$ hat als Wahrscheinlichkeit $\frac{1}{6}\approx 0.17$.

Wollen wir nun wissen, wie groß die Wahrscheinlichkeit ist, dass man beim Würfelwurf eine Zahl $\leq 3$ würfelt, so müssen wir $P(X\leq 3)$ berechnen: $$P(X\leq 3)=P(X=1)+P(X=2)+P(X=3)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{3}{6}$$

Definition

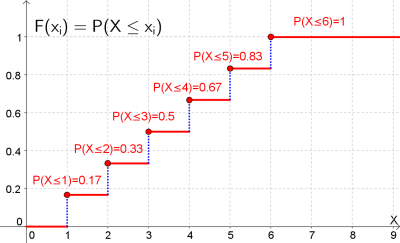
Die Verteilungsfunktion $F$ ist definiert als $F(x_i)=P(X\leq x_i)$. Sie gibt also immer die Wahrscheinlichkeit an, dass die Zufallsvariable $X$ einen Wert kleiner oder gleich dem Wert von $x_i$ annimmt.

Die folgende Graphik zeigt die Verteilungsfunktion für die Zufallsvariable $X$, die die Augenzahl beim zufälligen Wurf eines Würfels zählt:

Verteilungsfunktion $F$ für das Würfeln eines Würfels, wobei $X$ die Augenzahl angibt.

Hinweise zur Verteilungsfunktion:

Die Funktion $F$ macht aus folgenden Gründen immer Sprünge:

- die Wahrscheinlichkeit, dass eine Zahl kleiner als $1$ gewürfelt wird ($=P(X<1)$) ist $0$, somit sind alle Funktionswerte von $F$ links der $1$ gleich $0$.

- Bei $X=1$ macht die Verteilungsfunktion $F$ einen Sprung. Anschließend ist für alle $X<2$ die Wahrscheinlichkeit $P(X<2)=\frac{1}{6}\approx 0.17$ (die Wahrscheinlichkeit, dass eine Zahl kleiner als $2$ gewürfelt wird ist $\frac{1}{6}$).

- Bei $X=2$ macht die Funktion wieder einen Sprung um den Wert $\frac{1}{6}\approx 0.17$, da hier die Wahrscheinlichkeit für eine $2$ ($=P(X=2)=\frac{1}{6}$) hinzukommt.

- Ab $X=6$ hat die Verteilungsfunktion durchgängig den Wert $1$, da gilt $P(X<=6)=1$ (die Wahrscheinlichkeit, dass ein Wert kleiner oder gleich $6$ gewürfelt wird, ist $1$).

- Die Höhe der Sprünge entspricht gerade der Höhe der Funktionswerte bei der Wahrscheinlichkeitsfunktion (siehe oben).

Erwartungswert und Standardabweichung

Im Kapitel Beschreibende Statistik haben wir bereits Begriffe wie die relative Häufigkeit, das arithmetische Mittel und die Standardabweichung kennen gelernt. Auch in der Wahrscheinlichkeitsrechnung gibt es ähnliche Konzepte: Wahrscheinlichkeit, Erwartungswert und Standardabweichung:

Idee ...	In der Wahrscheinlichkeitsrechnung	in der Statistik
Prozent	Wahrscheinlichkeit $$P(X=x_i)$$	relative Häufigkeit $$h_i=\frac{H_i}{n}$$
Mittel/Durchschnitt	Erwartungswert $E(X)$ oder $\mu$ $$\mu=\sum_{i=1}^{n}x_i\cdot P(X=x_i)$$	Arithmetisches Mittel $$\bar{x}=\sum_{i=1}^{n}x_i\cdot h_i$$
Streuung/Abweichung vom Mittel	Standardabweichung $$\sigma=\sqrt{\sum_{i=1}^{n}(x_i-\mu)^2\cdot P(X=x_i)}$$	Standardabweichung $$\sigma=\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2\cdot h_i}$$

Berechnen Sie a) den Erwartungswert b) die Standardabweichung beim Wurf eines sechsseitigen Würfels, wobei die Zufallsvariable $X$ die Augensumme angibt (d. h. $X\in \{1;2;3;4;5;6\}$).

a) Zuerst machen wir uns eine Wertetabelle der Wahrscheinlichkeitsfunktion $f: f(x_i)=P(X=x_i)$:

Der Erwartungswert $E(X)=\mu=\sum_{i=1}^{n}x_i\cdot P(X=x_i)$. Setzen wir die Werte aus der Tabelle in die Formel ein, so erhalten wir: $$ \sum_{i=1}^{n}x_i\cdot P(X=x_i)=\underbrace{1}_{x_1}\cdot \underbrace{\frac{1}{6} }_{P(X=x_1) }+2\cdot \frac{1}{6} +3\cdot \frac{1}{6} +4 \cdot \frac{1}{6}+5\cdot \frac{1}{6}+6\cdot \frac{1}{6}=\underline{\underline{3.5} }$$

Der Erwartungswert $\mu$ beträgt also $3.5$. Natürlich kann man aber beim einmaligen Würfeln nicht $3.5$ würfeln. Man kann den Erwartungswert aber so interpretieren, dass, wenn man lange genug würfelt, der Durchschnitt bei $3.5$ liegen wird.

b) Die Standardabweichung $\sigma=\sqrt{\sum_{i=1}^{n}(x_i-\mu)^2\cdot P(X=x_i)}$

Setzen wir wieder alles in die Formel ein (siehe obige Wertetabelle und $\mu=3.5$): $$\sigma=\sqrt{\sum_{i=1}^{n}(x_i-\mu)^2\cdot P(X=x_i)}=\\ \sqrt{(1-3.5)^2\cdot \frac{1}{6}+(2-3.5)^2\cdot \frac{1}{6}+(3-3.5)^2\cdot \frac{1}{6}+(4-3.5)^2\cdot \frac{1}{6}+(5-3.5)^2\cdot \frac{1}{6}+(6-3.5)^2\cdot \frac{1}{6} }\\ =\underline{\underline{1.71} }$$

Exkurs: Kombinatorik - Die Kunst des Abzählens

siehe Binomialkoeffizient

Exkurs 2: Lotto

Mit dieser Überlegung können wir uns nun ganz einfach die Wahrscheinlichkeit für einen Lottogewinn berechnen. Beim Lotto werden insgesamt $6$ von $45$ Kugeln gezogen. Dabei ist die Reihenfolge egal.

Die Anzahl der möglichen Ziehungen ist somit $\binom{45}{6}=8.145.060$ (aus $45$ Kugeln werden $6$ gezogen).
Die Anzahl der günstigen Möglichkeiten $\binom{6}{6}=1$

Somit ist die Wahrscheinlichkeit für einen Lotto-$6$er: $$P(\text{Lotto-}6er)=\frac{günstige}{mögliche}=\frac{\binom{6}{6}}{\binom{45}{6}}=\frac{1}{8.145.060}$$

Berechnen Sie die Wahrscheinlichkeit, beim Lotto $5$ der $6$ richtigen Kugeln auszuwählen.

Die Anzahl der möglichen Ziehungen ist wieder $\binom{45}{6}=8.145.060$ (aus $45$ Kugeln werden $6$ gezogen).
Die Anzahl der günstigen Möglichkeiten $\binom{6}{5}=6$ (aus $6$ Kugeln werden $5$ gezogen) Mal $\binom{39}{1}$ (= aus $39$ Kugeln wird eine gezogen).

$$P(5er)=\frac{günstige}{mögliche}=\frac{\binom{6}{5}\cdot \binom{39}{1} }{\binom{45}{6} }=\frac{6\cdot 39}{8.145.060}\approx 0.00002873 \ \ (= 0.002873 \%)$$

Inhaltsverzeichnis

1 Bernoulli-Experimente und die Binomialverteilung
- 1.1 Definition und Formel
- 1.2 Typischer Graph der Wahrscheinlichkeitsfunktion
  - 1.2.1 Eigenschaften des Graphen
2 Zusammenfassende Videos
3 Berechnung mithilfe von Technologie
4 Musterbeispiel

Bernoulli-Experimente und die Binomialverteilung

Definition und Formel

Im Folgenden betrachten wir ein sogenanntes

Definition

Bernoulli-Experiment (benannt nach dem schweizer Mathematiker Jakob Bernoulli).

Dies sind Experimente, bei denen es

genau zwei mögliche Ergebnisse $E$ und $\bar{E}$ ($=$ nicht $E$) gibt und
sich die Wahrscheinlichkeit für die einzelnen Ereignisse nicht ändert, d. h. für alle Versuchsausgänge gilt $P(E)=p$ und $P(\bar{E})=1-p$.

Typische Beispiele hierfür wären:

Ziehen von roten und blauen Kugeln aus einer Urne mit Zurücklegen: Die Zufallsvariable $X$ zählt das Auftreten von roten Kugeln.
Mehrmaliges Würfeln mit einem Würfel: Die Zufallsvariable $X$ zählt das Auftreten eines $6er$.
Multiple-Choice-Tests: Die Zufallsvariable $X$ zählt die richtigen Antworten.

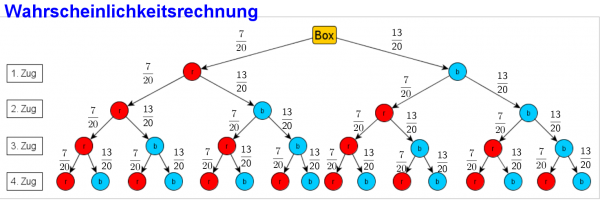
Sie stehen vor einer Urne mit $7$ roten und $13$ blauen Kugeln. Wie groß ist die Wahrscheinlichkeit, bei $4$-maligem Ziehen mit Zurücklegen, $3$-mal eine rote Kugel zu erhalten?

Die Zufallsvariable $X$ zählt die Anzahl der roten Kugeln. Gefragt ist also

$$P(X=3)=?$$

Baumdiagramm für das dreimalige Ziehen mit Zurücklegen aus einer Box mit $7$ roten und $13$ blauen Kugeln

Anzahl der Pfade zu unserem Ergebnis: Um von $4$ Ziehungen $3$-mal eine rote Kugel zu ziehen gibt es $\binom{4}{3}=4$ Möglichkeiten, nämlich:

$(r,r,r,b)$; $(r,r,b,r)$; $(r,b,r,r,)$; $(b,r,r,r)$.

Hinweis: $\binom{4}{3}$ (gesprochen „$4$ über $3$“) ist der sogenannte Binomialkoeffizient.

Die Wahrscheinlichkeit für dreimal rot und einmal blau ist bei jedem Pfad $p^3\cdot (1-p)^1$ mit $p=\frac{7}{20}$.

Begründung: Nehmen wir zum Beispiel $(r,r,r,b)$.

Die Wahrscheinlichkeit, eine rote Kugel zu ziehen ist $p=\frac{7}{20}$. Die Wahrscheinlichkeit eine blaue Kugel zu ziehen ist $(1-p)=\frac{13}{20}$. Somit ist die Wahrscheinlichkeit für das Ergebnis $(r,r,r,b)$ aufgrund der 1. Pfadregel/Multiplikationsregel $$p\cdot p\cdot p\cdot (1-p)=p^3\cdot (1-p)^1$$ Für die anderen Möglichkeiten $(r,r,b,r)$; $(r,b,r,r,)$ und $(b,r,r,r)$ kommt man auf dasselbe Resultat. Somit erhalten wir: $$P(X=3)=\underbrace{\binom{4}{3} }_{\textrm{Anzahl der Pfade} }\cdot \underbrace{p^3\cdot (1-p)^1}_{\textrm{Wahrscheinlichkeit für einen dieser Pfade} }=4\cdot (\frac{7}{20})^3\cdot \frac{13}{20}= 0.1115=11.15\%$$

Definition

Binomialverteilung und Formel

Es wird ein Bernoulli-Experiment ($2$ mögliche Ausgänge: Erfolg oder Misserfolg) $n$-mal durchgeführt, wobei die Erfolgswahrscheinlichkeit $p$ konstant bleibt.

Die Zufallsvariable $X$ zählt die Anzahl der Erfolge.

Dann ist $X$ binomialverteilt (kurz: $B(n;p)$) mit der Wahrscheinlichkeitsfunktion $$P(X=k)=\binom{n}{k}\cdot p^k\cdot (1-p)^{n-k}$$

Merke

Die Formel für die Wahrscheinlichkeitsfunktion der Binomialverteilung:

$$P(X=k)=\binom{n}{k}\cdot p^k\cdot (1-p)^{n-k}$$

setzt sich folgendermaßen zusammen:

$\binom{n}{k}...$ Anzahl der Möglichkeiten, dass von $n$ Versuchen der Erfolg insgesamt $k$-mal eintritt.
$p^k...$ Wahrscheinlichkeit, dass der Erfolg insgesamt $k$-mal eintritt.
$(1-p)^{n-k}...$ Wahrscheinlichkeit, dass der Erfolg insgesamt $n-k$-mal NICHT eintritt.

Merke

Für eine Zufallsvariable $X$, die $B(n;p)-$verteilt ist, gilt:

Erwartungswert: $E(X)=\mu=n\cdot p$

Der Erwartungswert ist jener Wert, den die Zufallsvariable $X$ im Mittel annimmt.

Standardabweichung: $\sqrt{n\cdot p\cdot (1-p) }$

Die Standardabweichung ist ein Maß für die im Mittel zu erwartende Abweichung der Zufallsvariable $X$ vom Erwartungswert $\mu$.

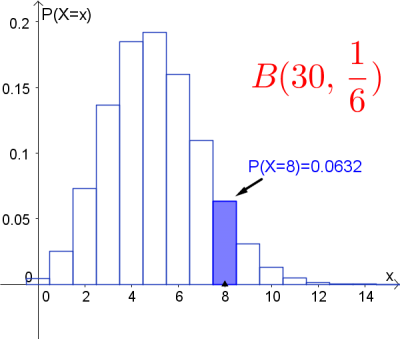
Ein Würfel wird $30$-mal geworfen.

a) Wie groß ist die Wahrscheinlichkeit $8$-mal eine $6$ zu würfeln?

b) Wie groß ist die Wahrscheinlichkeit niemals eine $6$ zu würfeln?

c) Wie groß ist die Wahrscheinlichkeit maximal einmal eine $6$ zu würfeln?

d) Wie groß ist die Wahrscheinlichkeit mindestens zweimal eine $6$ zu würfeln?

e) Bestimmen Sie den Erwartungswert und die Standardabweichung.

Die Zufallsvariable $X$ zähle das Vorkommen einer $6$. Da es sich um ein Bernoulli-Experiment handelt (zwei mögliche Ausgänge: $6$er oder kein $6$er und die Wahrscheinlichkeit für eine $6$ bleibt konstant mit $p=\frac{1}{6}$), ist $X$ binomialverteilt mit $n=30$ und $p=\frac{1}{6}$ und es gilt:

$$P(X=k)=\binom{30}{k}\cdot (\frac{1}{6})^k\cdot (\frac{5}{6})^{30-k}$$

a) Gesucht ist $P(X=8)$. Setzen wir das in die Formel ein, so erhalten wir: $$P(X=8)=\binom{30}{8}\cdot (\frac{1}{6})^8\cdot (\frac{5}{6})^{30-8}=0.0632=6.32\% $$ Hinweis: Zur Berechnung des Binomialkoeffizienten $\binom{30}{8}$ klicke hier.

Die Höhe des blauen Balkens gibt die Wahrscheinlichkeit für $8$ Sechser an.

b) Gesucht ist $P(X=0)$, dies kann entweder einfach über die 1. Pfadregel (Multiplikationsregel) mit $P(X=0)=(\frac{5}{6})^{30}=0.0042=0.42\%$ berechnet werden, oder mit der Formel für die Binomialverteilung: $$P(X=k)=\binom{30}{0}\cdot (\frac{1}{6})^0\cdot (\frac{5}{6})^{30-0}=0.0042=0.42\% $$

c) Gesucht ist $P(X\leq 1)$: $$P(X\leq 1)=P(X=0)+P(X=1)=\underbrace{0.0042}_{P(X=0)}+\underbrace{\binom{30}{1}\cdot (\frac{1}{6})^1\cdot (\frac{5}{6})^{30-1} }_{P(X=1)}=0.0042+0.0253=0.0295=2.95\% $$

Eingefärbt sind $P(X=0)$ und $P(X=1)$. Zusammen ergeben Sie die gesuchte Wahrscheinlichkeit $P(X\leq 1)$.

d) Betrachten wir die obige Abbildung von Aufgabe c). Dann ist die Wahrscheinlichkeit mindestens zweimal eine $6$ zu ziehen $(P(X\geq 2))$ gerade die weiß eingefärbte Fläche. Mithilfe der Gegenwahrscheinlichkeit erhalten wir: $$P(X\geq 2)=1-P(X\leq 1)=1-0.0295=0.9705=97.05\% $$

e)

$E(X)=n\cdot p=30\cdot \frac{1}{6}=5$ (Dies kann man auch aus den obigen Graphen herauslesen!)
$\sigma=\sqrt{n\cdot p\cdot (1-p)}=\sqrt{30\cdot \frac{1}{6}\cdot \frac{5}{6} }=\sqrt{\frac{25}{6} }\approx 2.04$.

Typischer Graph der Wahrscheinlichkeitsfunktion

Die Wahrscheinlichkeitsfunktion der Binomialverteilung wird in der Regel als Histogramm dargestellt.

$Aha!$ $\ $ Im folgenden Arbeitsblatt lernst du den Graphen einer binomialverteilten Zufallsvariable besser kennen.

Eigenschaften des Graphen

Rechtsschiefe Binomialverteilung mit $n=10$ und $p=0.2$. Damit ist $E(X)=2$ und $\sigma=1.26$
Symmetrische Binomialverteilung mit $n=10$ und $p=0.5$. Damit ist $E(X)=5$ und $\sigma=1.58$
Linksschiefe Binomialverteilung mit $n=10$ und $p=0.7$. Damit ist $E(X)=7$ und $\sigma=1.45$

Merke

Eigenschaften:

Die Höhe und Fläche eines Balkens geben die Wahrscheinlichkeit $P(X=k)$ an.
Die gesamte Fläche aller Balken beträgt $1$ ($=100 \%$). Rechnerisch: $\sum_{k=0}^{n} P(X=k)=1$
Der höchste Balken befindet sich immer beim Erwartungswert.
Je größer die Standardabweichung ist, desto flacher ist der Graph.
Ist $p\leq 0.5$, so ist der Graph rechtsschief.
Ist $p\geq 0.5$, so ist der Graph linksschief.

Zusammenfassende Videos

Berechnung mithilfe von Technologie

Wähle deine Technologie

Musterbeispiel

Eine Lehrerin erstellt für ihre Schülerinnen und Schüler einen Multiple-Choice-Test, der aus insgesamt $15$ Fragen besteht. Jede Frage beinhaltet $5$ Antwortmöglichkeiten, wobei nur eine davon korrekt ist. Nun fragt sie sich, welche Chancen ein Schüler hat, wenn er die Aufgaben nur zufällig ankreuzt:

a) Wie groß ist die Wahrscheinlichkeit genau $3$ Fragen zu beantworten?

b) Wie groß ist die Wahrscheinlichkeit maximal $2$ Fragen richtig zu beantworten?

c) Um den Test zu bestehen, benötigt ein Schüler mindestens $8$ Punkte. Wie groß ist die Wahrscheinlichkeit, den Test (bei zufälligem Ankreuzen) zu bestehen?

d) Wie groß ist die Wahrscheinlichkeit, dass ein Schüler zwischen $4$ und $7$ Punkte erhält?

e) Wie groß ist der Erwartungswert ($E(x)$ bzw. $\mu$) und die Standardabweichung $\sigma$? Interpretiere diese Werte.

$$ \ $$

$n=15$
$p=\frac{1}{5}=0.2$
Die Zufallsvariable $X$ zählt die Anzahl der richtigen Antworten.

a) Wie groß ist die Wahrscheinlichkeit genau $3$ Fragen zu beantworten?

Gesucht sind $k=3$ Erfolge: $$P(X=3)=\binom{15}{3}\cdot 0.2^3\cdot 0.8^{12}=0.2501=25.01\%$$ Mit dem TI-8x: $P(X=3)=binompdf(15,0.2,3)=0.2501$

Lösung von a) mithilfe von GeoGebra

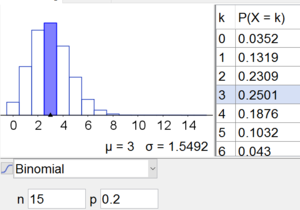
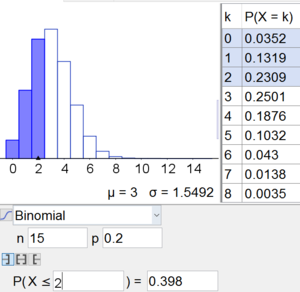
b) Wie groß ist die Wahrscheinlichkeit maximal $2$ Fragen richtig zu beantworten?

Gesucht ist $k\leq 2$: $$P(X\leq 2)=\text{Technologieeinsatz}=0.398=39.8\% $$ Mit dem TI-8x: $P(X\leq 2)=binomcdf(15,0.2,2)=0.398$

Lösung von b) mithilfe von GeoGebra

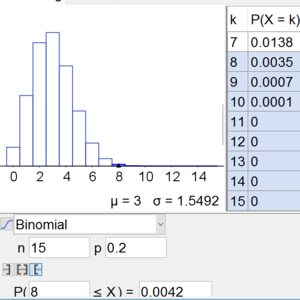
c) Um den Test zu bestehen, benötigt ein Schüler mindestens $8$ Punkte. Wie groß ist die Wahrscheinlichkeit, den Test (bei zufälligem Ankreuzen) zu bestehen?

Gesucht ist $k\geq 8$: $$P(X\geq 8)=\text{Technologieeinsatz}=0.0042=0.42\%$$ Mit dem TI-8x: $P(X\geq 8) = 1-P(X\leq 7)=1-binomcdf(15,0.2,7)=0.0042$

Lösung von c) mithilfe von GeoGebra

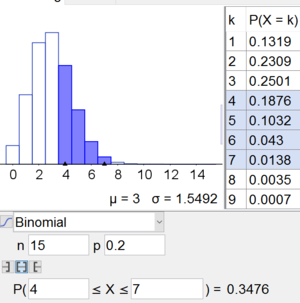
d) Wie groß ist die Wahrscheinlichkeit, dass ein Schüler zwischen $4$ und $7$ Punkte erhält?

$$P(4\leq X\leq 7)=\text{Technologieeinsatz}=0.3476=34.76\% $$ Mit dem TI-8x: $$P(4\leq X\leq 7)=P(X\leq 7)-P(X\leq 3)=$$ $$binomcdf(15,0.2,7)-binomcdf(15,0.2,4)=0.3476$$