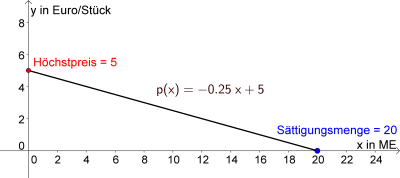Kosten- und Preistheorie

Die folgenden zwei Videos zeigen geben dir eine Zusammenfassung aller wichtigen Punkte der Kosten- und Preistheorie. Details zu den einzelnen Begriffen findest du unterhalb der Videos.

Auflistung aller wichtigen Begriffe	Beispiel

Inhaltsverzeichnis

[Verbergen]

1 Preisfunktion der Nachfrage
2 Erlösfunktion
- 2.1 Allgemein
- 2.2 Grenzerlös
3 Kostenfunktion
4 Gewinnfunktion
- 4.1 Allgemein
- 4.2 Der Cournot'sche Punkt
5 Übungs- und Überblicksdokumente
6 Maturaaufgaben

Preisfunktion der Nachfrage

Definition

Die Preisfunktion der Nachfrage, auch „Nachfragefunktion“ oder „Preis-Absatz-Funktion“ genannt, gibt den Preis

$p$ in Abhängigkeit der produzierten Menge

$x$ an.

Graph einer linearen Preisfunktion

Merke

Der Höchstpreis $p_h$ ist jener Preis, zu dem gerade kein Stück mehr verkauft werden kann. Es gilt:

$p_h=p(0)$

Die Sättigungsmenge $x_S$ ist jene Menge, bei dem der Markt gesättigt ist und damit nicht mehr verkauft werden kann. Hier gilt:

$p(x_S)=0$

Höchstpreis und Sättigungsmenge können mithilfe der Schnittpunkte der Preisfunktion $p$ mit den Achsen bestimmt werden.

[Ausklappen]

Eine Firma kann von ihrem Produkt $5$ Mengeneinheiten verkaufen, wenn sie den Preis auf $3.75€$ pro Stück festlegt. Senkt sie den Preis auf $2.50€$ pro Stück, so kann sie $10$ Mengeneinheiten des Produktes verkaufen.

Modellieren Sie die lineare Preisfunktion.
Ermitteln Sie daraus den Höchstpreis und die Sättigungsmenge.

$\$

Zuerst stellen wir die lineare Preisfunktion der Form $p(x)=k\cdot x+d$ auf, wobei $x$ die Mengeneinheiten und $p(x)$ den Preis pro Stück angibt.

Die Funktion kann mithilfe der beiden Punkte bestimmt werden.

1. Variante: Wir setzen die Punkte $(5\vert 3.75)$ und $(10\vert 2.50)$ in die Funktionsgleichung ein und berechnen $k$ und $d$ , indem wir das Gleichungssystem lösen (hierbei eignet sich z. B. das Additionsverfahren): $p(x)=k\cdot x+d$

1. Punkt:

$I:\ \ 3.75= k\cdot 5+d$

2. Punkt:

$\underline{II:2.50=k\cdot 10+d\ \ "-"}$

$\ \ \ \ 1.25=-5\cdot k\ \ \ \rightarrow k=-0.25 \rightarrow d=5$ Somit erhalten wir die Preisfunktion $p$ mit $p(x)=-0.25x+5$

Bestimmung der Funktionsgleichung mithilfe des Steigungsdreiecks.

2. Variante: Da es sich um eine lineare Funktion handelt, kann $k$ auch mithilfe des Steigungsdreiecks bei den Punkten $(5\vert 3.75)$ und $(10\vert 2.50)$ ermittelt werden: $k=\frac{\Delta y}{\Delta x}=\frac{Höhenunterschied}{Längenunterschied}=\frac{2.50-3.75}{10-5}=-0.25$ Somit ist $k=-0.25$ . Um $d$ zu berechnen, setzt man einen der beiden Punkte und $k$ in die Funktionsgleichung ein: Punkt $(5\vert 3.75)$ und $k=-0.25$ in $p(x)=k\cdot x+d$ eingesetzt ergeben: $3.75=-0.25\cdot 5+d$ $\rightarrow 3.75+1.25=d \rightarrow d=5$ Somit erhalten wir: $p(x)=-0.25\cdot x+5$

Nun bestimmen wir mit der Preisfunktion den Höchstpreis und die Sättigungsmenge:

Höchstpreis:

$p(0)=d=5$ .

Der Höchstpreis beträgt

$5€$ pro Mengeneinheit.

Sättigungsmenge:

$p(x)=0$

$0=-0.25x+5$ $-5=-0.25x$ $x=20$

Die Sättigungsmenge beträgt somit

$20$ Mengeneinheiten.

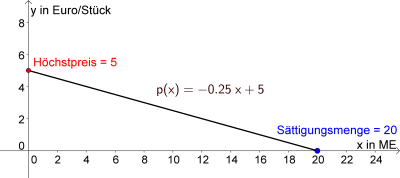
Preisfunktion mit Höchstpreis und Sättigungsmenge

Erlösfunktion

Allgemein

Definition

Der Gesamterlös

$E$ (auch Umsatz genannt) ergibt sich aus dem Produkt der verkauften Menge und dem dazugehörigen Preis:

$E(x)=x\cdot p(x)$

[Ausklappen]

Gegeben ist die Preisfunktion $p$ mit $p(x)=-0.25x+5$ .

Stellen Sie die dazugehörige Erlösfunktion auf.
Bestimmen Sie die sogenannten Erlösgrenzen, dies sind die Nullstellen der Erlösfunktion.
Berechnen Sie den maximalen Erlös.

$\$

Die Erlösfunktion erhalten wir mit:

$E(x)=x\cdot p(x)$ $E(x)=x\cdot (-0.25x+5$ $E(x)=-0.25x^2+5x$

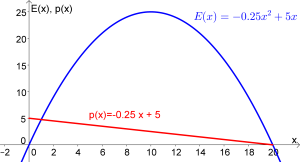
Graphen der Preis- und Erlösfunktion

Die Nullstellen ermitteln wir, indem wir die Erlösfunktion gleich null setzen:

$0=E(x)$ $0=-0.25x^2+5x$ Durch herausheben von $x$ , Quadkom oder den Löse-Befehl erhalten wir $x_1=0$ und $x_2=20$ .

Nun bestimmen wir den maximalen Erlös:

1. Variante: Mithilfe der Eigenschaften einer quadratischen Funktion.

Die Erlösfunktion $E$ mit $E(x)=-0.25x^2+5x$ ist eine quadratische Funktion mit $2$ Nullstellen. Wie jede quadratische Funktion hat sie aufgrund ihrer Symmetrie ihren Scheitelpunkt (Extremstelle) genau zwischen den beiden Nullstellen. $x_{max}=\frac{0+20}{2}=10$ Das Erlösmaximum befindet sich somit bei $x=10$ Mengeneinheiten. Der Erlös beträgt $E(10)=25$ Geldeinheiten.

2. Variante: Mithilfe des Maximum-Befehls (siehe Ti-Taschenrechner bzw. GeoGebra). Das Ergebnis siehst du in der rechten Abbildung

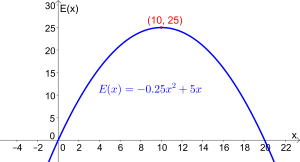
Erlösfunktion mit Erlösmaximum

3. Variante: Mithilfe der Differentialrechnung. Für ein Maximum muss gelten, dass $f'(x)=0$ und $f''(x)<0$ ist: $E'(x)=-0.5x+5$ $0=-0.5x+5\ \ \ \rightarrow x=10$ Und nun zur 2. Ableitung: $E''(x)=-0.5$ $E''(10)=-0.5<0 \ \ \ \rightarrow HP$ Somit befindet sich bei $x=10$ ein Hochpunkt und der Erlös an dieser Stelle beträgt $E(10)=25$ .

Grenzerlös

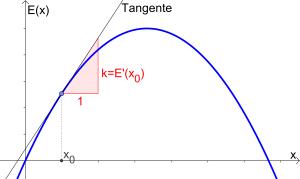
Graph der Erlösfunktion mit graphischer Bestimmung des Grenzerlöses

Definition

Der Grenzerlös

$E'(x)$ gibt die (ungefähre) Zunahme/Abnahme des Erlöses an, wenn eine weitere Mengeneinheit produziert wird.

[Ausklappen]

Bestimmen Sie den Grenzerlös der Erlösfunktion $E$ mit $E(x)=-0.25x^2+5x$ bei einer Menge von $x=5$ ME und interpretieren Sie das Ergebnis.

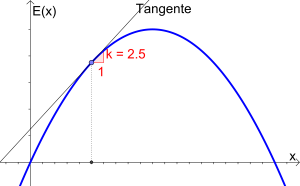
Bestimmen des Grenzerlöses

$E'(x)=-0.5x+5$

$E'(5)=-0.5\cdot 5+5$ $E'(5)=2.5 \textrm{ GE pro Mengeneinheit}$

Interpretation: Produziert man statt fünf Mengeneinheiten noch eine zusätzliche sechste, so steigt der Erlös (ungefähr) um $2.5$ Geldeinheiten.

[Ausklappen]

Hinweis!

Das „ungefähr“ wird deshalb verwendet, da die Tangente die Erlösfunktion nur bei

$x=5$ berührt und somit bei

$x=6$ ein leicht zu großer Wert herauskommt.

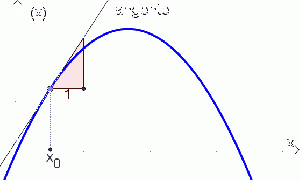
Der Grenzerlös ist nur eine Näherung an die tatsächliche Steigung der Erlösfunktion.

Kostenfunktion

Definition und Aufbau der Kostenfunktion

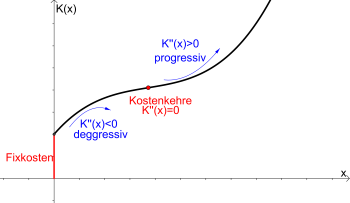
Graph einer „ertragsgesetzlichen“ Kostenfunktion

Definition

Die Gesamtkosten für die Produktion werden durch die Kostenfunktion

$K$ angegeben. Die Kostenfunktion besteht dabei aus

$2$ Termen:

$K(x)=K_v (x)+F$ $K_v (x)...$ variable Kosten (jene Kosten, die von der produzierten Menge $x$ abhängig sind)

$F...$ Fixkosten, die auch bei einer Produktion von $0$ ME anfallen.

Merke

Typische Eigenschaften einer "ertragsgesetzlichen Kostenfunktion"

Eine Kostenfunktion heißt ertragsgesetzlich, wenn sie
- streng monoton steigend ist (d. h. $K'(x)>0$ für alle $x$ im Definitionsbereich),
- zuerst einen degressiven Verlauf hat (d. h. rechtsgekrümmt ist, sprich $K''(x)<0$ ) und
- nach der Kostenkehre (Wendepunkt der Kostenfunktion, sprich $K''(x)=0$ )
- einen progressiven Verlauf hat (d. h. linksgekrümmt ist, sprich $K''(x)>0$ ).

[Ausklappen]

Gegeben ist die Kostenfunktion $K$ mit $K(x)=0.017x^3−0.38x^2+3.3x+10$ a) Bestimmen Sie die Fixkosten und die variablen Kosten der Funktion.
b) Berechnen Sie die Kosten bei einer Produktion von $12$ ME. Geben Sie auch an, wie hoch die variablen Kosten sind.
c) Ermitteln Sie die Produktionsmenge, wenn Kosten von $60$ GE anfallen.

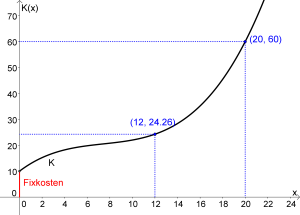
Graph der Kostenfunktion

$K$

a) Die Kostenfunktion lautet $K(x)=0.017x^3−0.38x^2+3.3x+10$ . Der konstante Term gibt die Fixkosten an, der Term mit den $x$ gibt die variablen Kosten an:

Fixkosten: $10$
Variable Kosten: $0.017x^3−0.38x^2+3.3x$

b) Gefragt sind die Kosten bei $x=12$ ME und gesucht ist $K(12)$ : $K(12)=0.017\cdot 12 ^3−0.38 \cdot 12^2+3.3\cdot 12+10=24.256 \textrm{ GE}$

c) Die Kosten betragen $K(x)=60$ und gesucht ist $x$ : $60=0.017x^3−0.38x^2+3.3x+10$ Mithilfe von Technologie (siehe TI-Befehle bzw. GeoGebra) erhalten wir: $x=20$ A: Bei einer Produktion von $20$ ME fallen Kosten von $60$ GE an.

Grenzkosten

Definition

Die Grenzkosten

$K'(x)$ geben die (ungefähre) Zunahme/Abnahme der Kosten an, wenn eine weitere Mengeneinheit produziert wird.

$K'(x)$ bezeichnet dabei die 1. Ableitung von

$K(x)$ .

Bild mit Tangente und Steigungsdreieck

[Ausklappen]

Gegeben ist die Kostenfunktion $K(x)=0.017x^3−0.38x^2+3.3x+10$

Bestimmen Sie die Grenzkosten bei einer Produktionsmenge von $20$ ME.
Interpretieren Sie das Ergebnis.

Die Grenzkosten ermitteln wir mithilfe der ersten Ableitung:

$K(x)=0.017x^3−0.38x^2+3.3x+10$ $K'(x)=0.051x^2-0.76x+3.3$ $K'(x)$ gibt uns die Grenzkostenfunktion an. Nun müssen wir nur noch die Grenzkosten bei $20$ ME, d. h. $K'(20)$ bestimmen: $K'(20)=0.051\cdot 20^2-0.76\cdot 20+3.3$ $K'(20)=8.5\textrm{ GE/ME}$ Die Grenzkosten bei einer Produktionsmenge von $x=20$ ME betragen $8.5$ GE/ME.

Interpretation: Bei einer Produktion von $20$ Mengeneinheiten fallen für eine zusätzlich produzierte $21$ . Mengeneinheit Kosten von ca. $8.5$ GE/ME an.

Stückkostenfunktion, Betriebsoptimum und langfristige Preisuntergrenze

Definition

Die Stückkosten

$\bar{K}(x)$ geben die durchschnittlichen Kosten pro Stück (oder Mengeneinheit) an und berechnen sich, indem die Gesamtkosten durch die Stückzahlen dividiert werden, d. h. mit

$\bar{K}(x)=\frac{K(x)}{x}$ $x...$ Anzahl der produzierten Stückzahlen (oder Mengeneinheiten).

$K(x)...$ Gesamtkosten

$\bar{K}(x)...$ durchschnittliche Kosten pro Stück/Mengeneinheit

Interessant bei den durchschnittlichen Kosten ist jene Stelle, bei der die Kosten pro Stück minimal sind. Diese Stelle nennt man das

Graph der Stückkostenfunktion mit Betriebsoptimum und langfristiger Preisuntergrenze

Merke

Betriebsoptimum $x_{opt}$

... ist jene Stelle, bei der die Stückkosten $\bar{K}(x)$ ein Minimum (Tiefpunkt) haben.

Die dazugehörigen Stückkosten $\bar{K}(x_{opt})$ nennt man langfristige Preisuntergrenze (oder auch kostendeckender Preis).

[Ausklappen]

Gegeben ist die Kostenfunktion $K$ mit $K(x)=0.017x^3 - 0.38x^2 + 3.3x + 10$

Berechnen Sie das Betriebsoptimum und die langfristige Preisuntergrenze.

Zuerst bestimmen wir die Stückkostenfunktion:

$K(x)=0.017x^3 - 0.38x^2 + 3.3x + 10$ $\bar{K}(x)=\frac{0.017x^3 - 0.38x2 + 3.3x + 10}{x}$ $\bar{K}(x)=0.017x^2 - 0.38x + 3.3 +\frac{10}{x}$ $\bar{K}(x)=0.017x^2 - 0.38x + 3.3+10x^{-1}$

Nun berechnen wir das Minimum der Stückkostenfunktion. Entweder mit dem Minimumbefehl (TI-Befehle,GeoGebra) oder (wie hier) mithilfe der Differentialrechnung (siehe Ableitung bestimmen bzw. Kurvendiskussionen):

Graph der Stückkostenfunktion

Um das Minimum zu berechnen, ermitteln wir zuerst $\bar{K}'(x)$ und setzen dies dann gleich $0$ : $\bar{K}'(x)=0.034x - 0.38 -10x^{-2}$ $0=0.034x - 0.38 -10x^{-2}\ \ \ \ \vert \cdot x^2$ $0=0.034x^3-0.38x^2-10$ Diese Gleichung löst man am besten graphisch (siehe TI-Befehle bzw. GeoGebra) oder mit dem Löse-Befehl (siehe TI-Befehle bzw. GeoGebra) und erhält: $x_{opt}=12.93$

Antwort: Das Betriebsoptimum liegt bei $12.93$ Mengeneinheiten.

Die dazugehörenden Stückkosten, die sogenannte langfristige Preisuntergrenze, liegen bei: $\bar{K}(x_{opt})=\bar{K}(12.93)= 2 \textrm{ GE pro ME}$

Variable Stückkostenfunktion, Betriebsminimum und kurzfristige Preisuntergrenze

Definition

Die variablen Stückkosten

$\bar{K_v}(x)$ geben die durchschnittlichen variablen Kosten pro Stück an.

$\bar{K_v}(x)=\frac{K_v(x)}{x}$

(Hinweis: $\bar{K_v}$ ist jener Term von $K(x)$ ohne die Fixkosten $F$ ).

Auch hier interessieren wir uns für jene Stelle, an der die variablen Stückkosten minimal sind:

Merke

Das Betriebsminimum $x_{min}$ ist jene Stelle, bei der die variablen Stückkosten minimal sind.

Die dazugehörenden variablen Stückkosten $\bar{K_v}(x_{min})$ werden kurzfristige Preisuntergrenze genannt.

[Ausklappen]

Gegeben ist die Kostenfunktion $K$ mit $K(x)=0.017x^3−0.38x^2+3.3x+10$ Bestimmen Sie

die variablen Kosten $K_v (x)$ ,
die variable Stückkostenfunktion $\bar{K_v}(x)$ sowie
das Betriebsminimum zusammen mit der kurzfristigen Preisuntergrenze.

* Die variable Kostenfunktion lautet

$K_v (x)=0.017x^3−0.38x^2+3.3x$

daraus erhalten wir die variable Stückkostenfunktion

$\bar{K_v}(x)=\frac{0.017x^3−0.38x^2+3.3x}{x}=0.017x^2−0.38x+3.3$

Nun müssen wir für das Betriebsminimum nur noch das Minimum der Stückkostenfunktion bestimmen:

$\bar{K_v}(x)=0.017x^2−0.38x+3.3$ $\bar{K_v}'(x)=0.034x-0.38$ $0=0.034x-0.38\ \rightarrow \underline{\underline{x_{min}= 11.18} }$ Das Betriebsminimum liegt somit bei $11.18$ Mengeneinheiten.

Zuletzt berechnen wir noch die kurzfristige Preisuntergrenze $\bar{K_v}(x_{min})$ : $\bar{K_v}(x)=0.017x^2−0.38x+3.3$ $\bar{K_v}(11.18)=0.017\cdot 11.18^2−0.38\cdot 11.18+3.3$ $\underline{\underline{\bar{K_v}(x)=1.18} }$ Die kurzfristige Preisuntergrenze beträgt somit $1.18$ GE und wird erreicht, wenn $x_{min}=11.18$ ME produziert werden.

Gewinnfunktion

Allgemein

Mithilfe des Erlöses (Umsatz) und der Kosten können wir nun den Gewinn berechnen:

Gewinnanalyse

Definition

Sei

$x$ die Menge der produzierten und zugleich verkauften Mengeneinheiten, dann erhält man den Gewinn

$G$ aus

$G(x)=E(x)-K(x)$ Der Gewinn ergibt sich, wenn man vom Erlös die Kosten abzieht.

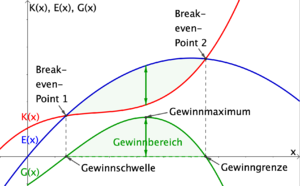
Folgende Punkte sind bei der Analyse der Gewinnfunktion relevant:

Merke

Der Break-even-Point ist jener Punkt, bei dem der Gewinn das erste Mal nicht mehr negativ ist (= 1. Nullstelle der Gewinnfunktion).
Der Gewinnbereich (auch Gewinnzone genannt) ist jenes Intervall, bei dem der Gewinn $G(x)>0$ ist.
Das Gewinnmaximum $G_{max}$ wird mithilfe des Hochpunktes der Gewinnfunktion bestimmt.
Der Grenzgewinn $G'(x)$ gibt die momentane Änderung des Gewinns an.

[Ausklappen]

Gegeben sind die Kosten- und die Preisfunktion eines Betriebes: $K(x)=0.017x^3−0.38x^2+3.3x+10$ $p(x)=−0.25x+5$ a) Ermitteln Sie die Gewinnfunktion.
b) Bestimmen Sie den Gewinnbereich.
c) Berechnen Sie das Gewinnmaximum.
d) Fertigen Sie eine Skizze der Gewinnfunktion an und markieren Sie den Gewinnbereich, den Break-even-Point und das Gewinnmaximum.
e) Ermitteln Sie graphisch die Steigung der Gewinnfunktion bei $x=7$ ME. Überprüfen Sie Ihr Ergebnis rechnerisch.

a) Die Gewinnfunktion wird aus der Differenz der Erlösfunktion (

$E(x)=x\cdot p(x)$ ) und der Kostenfunktion bestimmt:

$G(x)=E(x)-K(x)$ $G(x)=x\cdot (-0.25x+5)-(0.017x^3−0.38x^2+3.3x+10)$ $G(x)=-0.25x^2+5x-0.017x^3+0.38x^2-3.3x-10$ $\underline{G(x)=-0.017x^3+0.13x^2+1.7x-10}$

b) Der Gewinnbereich ist jener Bereich, wo $G(x)\geq 0$ gilt. Somit bestimmen wir zuerst die Nullstellen mit $G(x)=0$ . $G(x)=-0.017x^3+0.13x^2+1.7x-10$ $0=-0.017x^3+0.13x^2+1.7x-10$ Mithilfe von Technologie (für den TI-Taschenrechner eignet sich hier der zero-Befehl) erhalten wir: $\underline{x_1=5.22 \textrm{ und } x_2=11.90}$ Somit ist der Gewinnbereich das Intervall $[5.22;11.90]$ .

c) Das Gewinnmaximum erhalten wir, indem wir den Hochpunkt der Gewinnfunktion bestimmen. Somit müssen wir zuerst die erste Ableitung bestimmen und dann die Gleichung $G'(x)=0$ lösen: $G(x)=-0.017x^3+0.13x^2+1.7x-10$ $G'(x)=-0.051 x² + 0.26x + 1.7$ $0=-0.051 x² + 0.26x + 1.7$ Lösen wir die quadratische Gleichung (z. B. mit der großen Lösungsformel oder mit Quadkom), so erhalten wir: $x_1=-3.76 \textrm{ und } x_2=8.86$ Da eine negative Menge für den maximalen Gewinn nicht infrage kommt, bleibt nur noch $x_2=8.86$ als mögliche Stelle für das Gewinnmaximum übrig. Ob sich hier wirklich ein Hochpunkt befindet, können wir z. B. mithilfe der 2. Ableitung herausfinden: $G''(x)=-0.102 x + 0.26$ $G''(8.86)=-0.102 8.86 + 0.26 <0 \rightarrow \textrm{ Hochpunkt}$ Somit befindet sich der maximale Gewinn bei $x_{max}=8.86$ ME. Der maximale Gewinn beträgt: $G(x_{max})=G(8.86)=-0.017\cdot 8.86^3+0.13\cdot 8.86^2+1.7\cdot 8.86-10=3.44\textrm{ GE}$

d) Mithilfe des Gewinnbereichs und des Gewinnmaximums bei $(8.86\vert 3.44)$ und ein paar weiterer berechneter Punkte (siehe Wertetabelle) erhalten wir den Graphen der Gewinnfunktion:

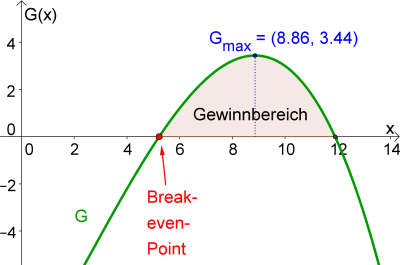
Graph der Gewinnfunktion mit Gewinnbereich, dem Break-even-Point und dem Gewinnmaximum

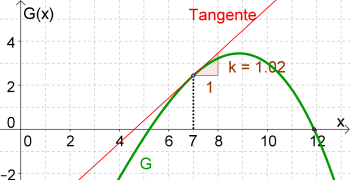
Tangente an die Gewinnfunktion bei x=7

e) Zeichnet man die Tangente an die Gewinnfunktion bei $x=7$ und anschließend das Steigungsdreieck ein, so erhält man eine Steigung von ca. $1$ .

Rechnerisch erhalten wir die Steigung mithilfe der 1. Ableitung an der Stelle $x=7$ : $G'(x)=-0.051 x² + 0.26x + 1.7$ $G'(7)=1.02$ Erhöht man die Produktionsmenge bei $x=7$ um eine weitere Einheit, so beträgt der zusätzliche Gewinn ca. $1.02$ GE (= Grenzgewinn bei $x=7$ ).

Der Cournot'sche Punkt

Graph der Preisfunktion mit dem Cournot'schen Punkt

$(x_{max}\vert p(x_{max}))$

Merke

Der Cournot'sche Punkt

Sei $x_{max}$ jene Menge, bei der der Gewinn maximal ist und $p(x_{max})$ der Preis bei dieser Menge. Dann bezeichnet der Punkt $(x_{max} \vert p(x_{max}))$ den Cournot‘schen Punkt. Dieser liegt auf dem Graphen der Preisfunktion $p$ .

Der Cournot'sche Punkt gibt somit an, bei welcher Menge der maximale Gewinn liegt und wie groß der Preis sein muss.

[Ausklappen]

Der Preis ist gegeben durch die Preisfunktion $p$ mit $p(x)=−0.25x+5$ Durch Analyse der Gewinnfunktion weiß das Unternehmen, dass der maximale Gewinn bei einer Menge von $x_{max}=8.86$ erzielt wird.

a) Berechnen Sie den dazugehörigen Preis pro Mengeneinheit, bei dem der maximale Gewinn erreicht wird.
b) Bestimmen Sie die Koordinaten des Cournot'schen Punktes.

In den Graphen der Preisfunktion

$p$ wurde der Cournot'sche Punkt eingezeichnet.

a) Indem wir für $x_{max}=8.86$ in die Preisfunktion einsetzen, erhalten wir den passenden Preis: $p(8.86)=−0.25\cdot 8.86+5$ $p(8.86)=2.785$ Der maximale Gewinn wird bei einem Preis von $2.785$ GE/ME erreicht.

b) Die Koordinaten des Cournot'schen Punktes lauten $P(x_{max}\vert p(x_{max})=(8.86\vert 2.785))$ Dieser kann im Graphen der Preisfunktion markiert werden (siehe Abbildung rechts).