Ableitung bestimmen

[+/-]

Widgets

Widgets

Letzte Änderungen
Gewünschte Seiten
  • Keine Informationen verfügbar
Wer ist online?
  • Es ist niemand angemeldet.
Aus Matura Wiki
Wechseln zu: Navigation, Suche

In den folgenden Abschnitten geht es darum, die erste Ableitung $f'(x)$ einer Funktion $f(x)$ zu bestimmen. Doch zuerst wiederholen wir noch einmal die Definition von f':

Vorausgesetzt sei im Folgenden, dass die Funktion $f(x)$ auf ihrem Definitionsbereich immer differenzierbar ist (d.h. $f'(x)$ existiert). Dies muss, streng mathematisch genommen, vorausgesestzt werden.

Definition
Grün rufezeichen.png
 Die Ableitungsfunktion $f'(x)$ ist der sogenannte Differentialquotient von $f(x)$

$$ f'(x)={k}=\lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{(x+\Delta x)- x} $$

und gibt die momentane Steigung der Funktion $f$ an der Stelle $x$ an.


$f'(x)$ wird auch als 1. Ableitung von $f(x)$ bezeichnet.


Der Differentialquotient $f'(x)$ berechnet die Steigung der Tangente $t$ und damit die Steigung von $f$ an der Stelle $x$.



Die Ableitungsfunktion $f'(x)$ kann allein durch Betrachtung der ursprünglichen Funktion $f(x)$ graphisch bestimmt werden.

Das folgende Applet zeigt dir den Zusammenhang zwischen einer Funktion und ihrer Ableitungsfunktion. Verschiebe dazu den Punkt $P$ in der linken Graphik:



Aufgaben zu diesem Applet

Betrachte die linke Graphik: Der Wert $k$ zeigt die Steigung der Tangente im Punkt $P$ an.

1. Verschieben Sie den Punkt $P$. Auf der rechten Graphik wird laufend die Steigung $k$ beim jeweiligen $x$-Wert von $P$ abgetragen. Verschieben Sie $P$ solange, bis in der rechten Graphik ein schöner Funktionsgraph zu sehen ist. Dieser Graph ist der Graph von $f'(x)$ (=1. Ableitung von $x$).

2. Geben Sie eine andere Funktion im Eingabefeld ein. Versuchen Sie den Graphen von $f'(x)$ zuerst zu erraten und zeichnen Sie ihn erst dann durch Verschieben des Punktes $P$.

Funktionen zum Eintippen:
a) $f(x)=1.5x^3-4x^2$
b) $f(x)=0.05x^4-0.225x^3-0.325x^2+0.9x+0.5$
c) $f(x)=3x$



Merke
Rotes rufezeichen.png
 $f'(x)$ gibt die Steigung von $f(x)$ an. Somit muss gelten:


$f(x)$ $f'(x)$
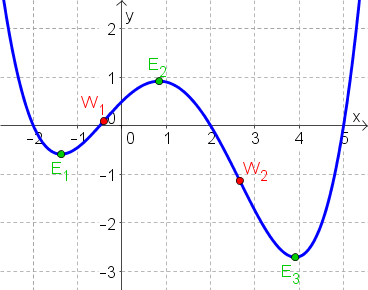
1. $f(x)$ hat bei $a$ eine Extremstelle $\rightarrow$ Hier ist die Steigung $f'(a)=0$
2. $f(x)$ hat bei $b$ einen Wendepunkt $\rightarrow$ Hier ist der Graph lokal am steilsten oder am flachsten $\rightarrow$ die Steigung $f'$ hat hier einen Hoch- oder Tiefpunkt $\rightarrow$ $f''(b)=0$
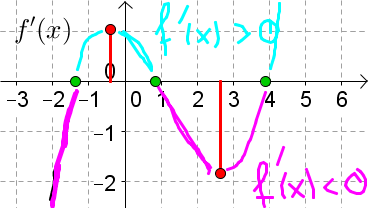
3. $f(x)$ ist monoton wachsend $\rightarrow$ $f'(x)$ ist positiv, d. h. oberhalb der $x$-Achse.
4. $f(x)$ ist monoton fallend $\rightarrow$ $f'(x)$ ist negativ, d. h. unterhalb der $x$-Achse.


Bsp.png

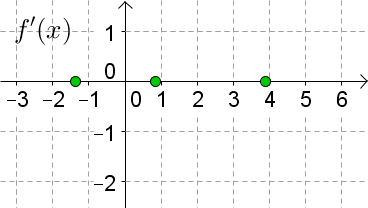
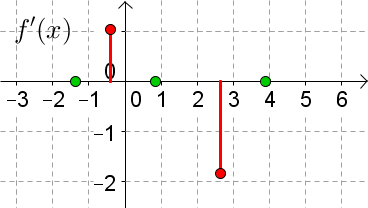
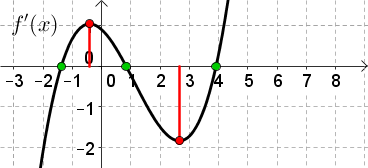
Skizzieren Sie zum gegebenen Graphen von $f(x)$ den Graphen von $f'(x)$.

Graph von f(x)

1. Schritt: Zeichne die Nullstellen von $f'(x)$ (= Extremwerte von $f(x)$) ein.
2. Schritt: Zeichne die Extremwerte von $f'(x)$ (= Wendepunkte von $f(x)$ ein. Die Höhen entsprechen den Steigungen von $f(x)$ bei den Wendepunkten.
3. und 4. Schritt: Aufgrund des Monotonieverhaltens von $f(x)$ wissen wir, wann $f'(x)$ positiv oder negativ ist.
$f'(x)$ schön eingezeichnet




Überprüfe dein Wissen

Im Folgenden sind Regeln aufgelistet, mit der $f'(x)$ berechnet werden kann.

Allgemeine Regeln



Regel $f(x)$ $f'(x)$ Bemerkung
Potenzregel $x^n$ $n\cdot x^{n-1}$ Der Exponent kommt herunter, dann wird die Hochzahl um $1$ vermindert.
Konstantenregel

$c\in \mathbb{R}$

$c$ $0$ Konstante Funktionen haben die Steigung $= 0$.
Faktorregel

$a\in \mathbb{R}$

$a\cdot f(x)$ $a\cdot f'(x)$ Ein konstanter Faktor ist von der Ableitung nicht betroffen.
Summenregel $f(x)+g(x)$ $f'(x)+g'(x)$ Eine Summe wird abgeleitet, indem jeder einzelne Summand einzeln abgeleitet wird.
$e$-Funktion $e^x$ $e^x$ Die besondere Eigenschaft von $e^x$ ist, dass es durch Ableiten nicht verändert wird.

(d. h. Funktionswert bei $x$ = Steigung bei $x$)

Logarithmus $ln|x|$ $\frac{1}{x}$
Trigonometrische Funktionen $\sin(x)$

$\cos(x)$ 		$\cos(x)$

$-\sin(x)$
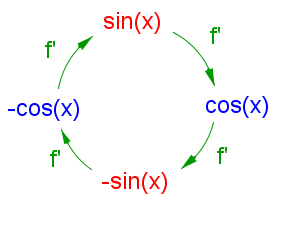Durch mehrmaliges Ableiten der Sinus- oder Cosinusfunktion kommt man immer wieder zur Ausgangsfunktion zurück. In diesem Arbeitsblatt findest du eine Begründung dafür.


Bsp.png

Bestimme zu den folgenden Funktionen die Ableitungsfunktion:

  1. $f(x)=x^3$
  2. $f(x)=4x$
  3. $f(x)=3$
  4. $f(x)=5\cdot x^2$
  5. $x^3+5x^2-4x+3$
  6. $x+\frac{1}{x}-\frac{1}{x^3}+\sqrt[5]{x^2}$
  7. $f(x)=\frac{x^4}{5}+2\cdot e^x-ln\vert x\vert $


Wir wenden die einzelnen Regeln Schritt für Schritt an:
  1. $f(x)=x^3 \rightarrow f'(x)\underbrace{=}_{Potenzregel} 3\cdot x^{3-1}=3\cdot x^2$

  2. $f(x)=4\cdot x=4\cdot x^1 \rightarrow f'(x)\underbrace{=}_{Potenzregel} 4\cdot 1\cdot x^{1-1}=4\cdot x^0=4\cdot 1=4$

  3. $f(x)=3 \rightarrow f'(x)\underbrace{=}_{Konstantenregel} 0$

  4. $f(x)=5\cdot x^2\rightarrow f'(x)\underbrace{=}_{Faktorregel}5\cdot (x^2)' \underbrace{=}_{Potenzregel}=5\cdot 2\cdot x^{2-1}=10\cdot x$

  5. $x^3+5x^2-4x+3\rightarrow f'(x)\underbrace{=}_{Summenregel}(x^3)'+(5x^2)'-(4x)'+(3)' \underbrace{=}_{Potenzregel}3x^2+10x-4+0$

  6. $x+\frac{1}{x}-\frac{1}{x^3}+\sqrt[5]{x^2}\underbrace{=}_{umformen} x+x^{-1}-x^{-3}+x^{\frac{2}{5} }$

    $$\rightarrow f'(x)\underbrace{=}_{Potenzregel}1\cdot x^0+(-1)\cdot x^{-2}-(-3)\cdot x^{-4}+\frac{2}{5}\cdot x^{(\frac{2}{5}-1)}=$$ $$=1-x^{-2}+3\cdot x^{-4}+\frac{2}{5}\cdot x^{-\frac{3}{5} }$$ $$=1-\frac{1}{x^2}+\frac{3}{x^4}+\frac{2}{5\sqrt[5]{x^3} }$$

  7. $f(x)=\frac{x^4}{5}+2\cdot e^x-ln \vert x \vert \rightarrow f'(x)\underbrace{=}_{Potenzregel/Faktorregel,\ e-\ und\ ln-Regel}\frac{4x^3}{5}+2\cdot e^x-\frac{1}{x}$


Weitere Übungen

Ordne im folgenden Applet Funktionen und ihre Ableitungen zu.

? $\ $ Online-Übung (mathe-online)

Produktregel

Im Gegensatz zur Summe zweier Funktionen $( f(x)+g(x))'=f'(x)+g'(x)$, siehe oben 'Summenregel'$)$ kann man das Produkt zweier Funktionen $f(x)\cdot g(x)$ nicht mehr so einfach ableiten. Hierfür braucht es die sogenannte ...


Merke
Rotes rufezeichen.png
 Produktregel

$$(f(x)\cdot g(x))'=f'(x)\cdot g(x)+f(x)\cdot g'(x)$$ „Zuerst den ersten Faktor ableiten, den zweiten stehen lassen, $$\textrm{Plus}$$ den ersten Faktor stehen lassen, den anderen ableiten.“



Bsp.png

Gegeben ist die Funktion $h(x)=(x^2-1)\cdot (3x^2-4x+1)$. Bestimmen Sie $h'(x)$.

Da es sich hierbei um ein Produkt handelt, müssen wir die Produktregel anwenden:

$$h(x)=\underbrace{(x^2-1)}_{f(x)} \cdot \underbrace{(3x^2-4x+1)}_{g(x)}$$ Zuerst berechnen wir in einer Nebenrechnung die Ableitungen der Faktoren: $$f(x)=x^2-1\rightarrow f'(x)=2x$$ $$g(x)=3x^2-4x-+1\rightarrow g'(x)=6x-4$$

Nun setzen wir die Formel zusammen: $$h'(x)=\underbrace{2x}_{f'(x)}\cdot \underbrace{(3x^2-4x+1)}_{g(x)}+\underbrace{(x^2-1)}_{f(x)}\cdot \underbrace{(6x-4)}_{g'(x)}$$

Zuletzt vereinfachen wir noch das Ergebnis: $$h'(x)=6x^3-8x^2+2x+6x^3-4x^2-6x+4$$ $$\underline{\underline{h'(x)=12x^3-12x^2-4x+4} }$$


Quotientenregel

Um die Ableitung einer Division von $2$ Funktionen (= Quotienten) zu berechnen, verwendet man die ...


Merke
Rotes rufezeichen.png
 Quotientenregel

$$h(x)=\frac{f(x)}{g(x)}\ \rightarrow \ h'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{(g(x))^2 }$$

Im Zähler steht bis auf das $Minus$ die Produktregel. Im Nenner wird die Nenner-Funktion quadriert.



Bsp.png

Bestimmen Sie die Ableitung von $h(x)=\frac{x^2-x}{x+1}$.

Da es sich um einen Quotienten handelt, wenden wir die Quotientenregel an. Zuerst berechnen wir die Ableitung des Zählers ($f(x)$) und des Nenners ($g(x)$):
  • Zähler: $f(x)=x^2-x\ \rightarrow f'(x)=2x-1$
  • Nenner: $g(x)=x+1\ \rightarrow g'(x)=1$

Nun setzen wir die Quotientenregel zusammen: $$h'(x)=\frac{(2x-1)\cdot (x+1)-(x^2-x)\cdot 1 }{(x+1)^2}$$ $$h'(x)=\frac{2x^2+x-1-x^2+x}{x^2+2x+1}$$ $$h'(x)=\frac{x^2+2x-1}{x^2+2x+1}$$


Kettenregel

Um Klammerausdrücke oder verkettete Funktionen wie zum Beispiel $f(x)=\sqrt[3]{x^2-1}$ oder $e^{2x-1}$ abzuleiten, verwenden wir die ...


Merke
Rotes rufezeichen.png
 Kettenregel

$$h(x)=f[g(x)]\ \ \rightarrow \ \ h'(x)=\underbrace{f'(g(x))}_{\textrm{äußere Ableitung} } \cdot \underbrace{g'(x)}_{\textrm{innere Ableitung} }$$

$f(x)$ wird als äußere Funktion, $g(x)$ als innere Funktion bezeichnet.


Bsp.png

Gegeben ist $h(x)=\sqrt[3]{x^2-1}$. Bestimmen Sie $h'(x)$.

Zuerst schreiben wir die Wurzel in der Exponentenschreibweise:

$$h(x)=(x^2-1)^{\frac{1}{3} }$$

  • Die äußere Funktion ist nun $f(x)=(\ \ )^{\frac{1}{3} }$. Damit ist $f'(x)=\frac{1}{3}\cdot (\ \ )^{\frac{1}{3}-1}=\frac{1}{3}\cdot (\ \ )^{-\frac{2}{3} }$
  • Die innere Funktion ist $g(x)=x^2-1$. Damit ist $g'(x)=2x$.

Nun setzen wir die Kettenregel zusammen: $$ h'(x)=\underbrace{\frac{1}{3}\cdot (x^2-1)^{-\frac{2}{3} } }_{\textrm{äußere Ableitung} } \cdot \underbrace{2x}_{\textrm{innere Ableitung} }$$

$$ h'(x)=\frac{2x}{3\cdot \sqrt[3]{(x^2-1)^2} }$$



Bsp.png

Bestimmen Sie die Ableitungsfunktion von $f(x)=e^{2x-1}$.

Zuerst kümmern wir uns um die äußere und innere Funktion getrennt:
  • Die äußere Funktion ist die Exponentialfunktion $f(x)=e\textrm{^}\ \rightarrow\ f'(x)=e\textrm{^}$.
  • Die innere Funktion ist $g(x)=2x-1 \ \rightarrow g'(x)=2$.

Nun setzen wir die Kettenregel wieder zusammen:

$$ h'(x)=\underbrace{e^{2x-1} }_{\textrm{äußere Ableitung} } \cdot \underbrace{2}_{\textrm{innere Ableitung} }$$ $$h'(x)=2\cdot e^{2x-1} $$


Produkt-, Quotienten- und Kettenregel Ableitung der Exponentialfunktion


Quiz: Einfache Regeln des Differenzierens (AN 2.1)


Quiz: Begriff Ableitungsfunktion/Stammfunktion (AN 3.1)


Quiz: Grafischer Zusammenhang zwischen Funktion und Ableitungsfunktion (AN 3.2)


Von „https://3.vobs.at/maturawiki/index.php?title=Ableitung_bestimmen&oldid=8481“