Wendepunkt und Wendetangente

Wendepunkt und Wendetangente

Funktion mit Wendepunkt W und Wendetangente

Definition

$ $ Ein Wendepunkt ist ein Punkt, in dem die Funktion f ihr Krümmungsverhalten ändert. Das heißt: Die Funktion geht von einer Rechtskrümmung in eine Linkskrümmung über (oder umgekehrt). Die Tangente durch den Wendepunkt heißt Wendetangente.

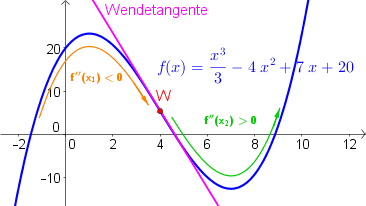
Wie erkennt man einen Wendepunkt?

Stell dir vor, der Graph ist eine Straße und du würdest die Straße mit einem Auto von links nach rechts entlangfahren. Zuerst kommt eine Rechtskurve, in der du das Lenkrad nach rechts drehst. Anschließend kommt eine Linkskurve, in der du das Lenkrad nach links drehen musst. Genau zwischen der Rechts- und der Linkskurve gibt es einen Moment, in dem das Lenkrad gerade ist - das ist der Wendepunkt.

Hinreichende Bedingung für einen Wendepunkt

Merke

Die Funktion $f(x)$ hat bei $x_0$ einen Wendepunkt, wenn gilt: $f''(x_0)=0 \quad$ UND $f'''(x)\ne 0$

Musterbeispiel

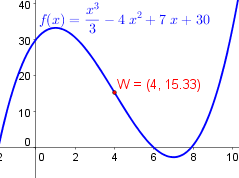
Bestimme den Wendepunkt und die Wendetangente der Funktion $\ f(x)=\frac{x^3}{3}-4x^2+7x+30$.

1. Wendepunkt

Zuerst bestimmen wir die zweite Ableitung $f''(x)$ und die dritte Ableitung $f'''(x)$: $$f(x)=\frac{x^3}{3}-4x^2+7x+30$$ $$f'(x)=x^2-8x+7$$ $$f''(x)=2x-8$$ $$f'''(x)=2$$

Nun setzen wir die zweite Ableitung $= 0$:

$$f''(x)=2x-8$$ $$0=2x-8$$ $$x=4$$

Somit ist die Stelle $x=4$ ein möglicher Wendepunkt. Um zu überprüfen, ob es sich wirklich um einen handelt, müssen wir den $x$-Wert in die dritte Ableitung einsetzen:

Graph mit Wendepunkt

$$f'''(x)=2$$ Da die dritte Ableitung konstant $=2$ ist (d. h. für alle $x$ den Wert $2$ hat), gilt insbesondere $$f'''(4)=2\ne 0$$ Somit ist an der Stelle $x=4$ ein Wendepunkt.

Um die $y$-Koordinate des Wendepunktes zu bestimmen, setzen wir in die ursprüngliche Funktion $f(x)$ ein, und erhalten: $$f(4)=\frac{4^3}{3}-4\cdot4^2+7\cdot 4+30=15.33$$

Somit hat der Wendepunkt die Koordinaten $W(4|15.33)$.

2. Wendetangente

$\rightarrow$ Siehe hier auch: Bestimmen der Tangente

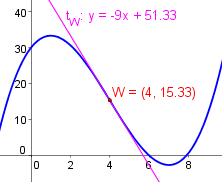
Um die Wendetangente $t_W: y=k\cdot x+d$ zu berechnen, brauchen wir zwei Sachen:

1. den Wendepunkt (diesen haben wir schon zuvor berechnet: $W(4|15.33)$)
2. die Steigung der Wendetangente - diese berechnen wir jetzt:

Die Steigung $k$ der Wendetangente ist ident mit der Steigung der Funktion am Wendepunkt. Somit müssen wir die Steigung von $f(x)$ beim Wendepunkt $W(4|15.33)$ berechnen und dies macht man immer mit der 1. Ableitung $f'(x)$:

$$f'(x)=x^2-8x+7$$ $$f'(4)=4^2-8\cdot 4+79$$ $$f'(4)=-9$$

Somit ist $k=-9$

Graph mit Wendepunkt und Wendetangente

Um das $d$ zu berechnen, setzen wir nun $k=-9$ und die Koordinaten des Wendepunktes $W(\underbrace{4}_{x}|\underbrace{15.33}_{y})$ in die $y=kx+d$-Darstellung und erhalten: $$y=kx+d$$ $$15.33=-9\cdot 4+d$$ $$d=51.33$$

Somit lautet die Gleichung der Wendetangente: $$\underline{\underline{t_W: \ y=-9\cdot x+51.33}}$$

Merke

Maximale oder minimale Steigung Am Wendepunkt befindet sich ein lokales Extremum der Steigung $f'(x)$. Das bedeutet, dass am Wendepunkt sich entweder a) ein lokales Maximum der Steigung (der Graph ist hier (in einem Bereich) am steilsten) oder b) ein lokales Minimum der Steigung (der Graph ist hier (in einem Bereich) am flachsten) befindet. Begründung: Am Wendepunkt gilt für die erste Ableitung von $f'$: $$(f'(x))'=f''(x)=0)$$ und für die zweite Ableitung von $f'$: $$(f'(x))''=f'''(x)\neq 0$$ Somit hat $f'$ hier einen Hoch- oder Tiefpunkt.