Regression
Die Regression ist eine Methode in der Statistik, den Zusammenhang (= Korrelation) zwischen zwei Merkmalen zu überprüfen.
Inhaltsverzeichnis
Einleitung
Sind zwei metrische Merkmale gegeben (z. B. Alter und Verdienst in einer Firma), so kann mithilfe der Regression der Zusammenhang dieser Merkmale überprüft und beschrieben werden.
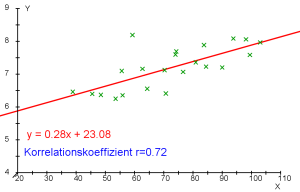
Zuerst werden die Merkmale in einer Punktwolke dargestellt.
Die Regression versucht nun, den Graphen einer Funktion „möglichst gut“ durch diese Punkte zu legen.
„Möglichst gut“ bedeutet dabei, dass die Summe der Quadrate der $y$-Abstände zwischen Funktion und Punkten so gering wie möglich sein soll.
$Aha!$ $\ $ Dieses Arbeitsblatt zeigt dir die grundlegende Idee am Beispiel einer linearen Regression, bei der die „bestmögliche“ Gerade gesucht ist:
Was bei diesem Applet zu tun ist:
1. Hake das Kästchen „Gerade“ an.
2. Nun kannst du dir die vertikalen Abstände der Punkte zur Geraden und die Abstandsquadrate anzeigen lassen.
3. Verschiebe die blauen Punkte auf der Geraden so, dass die Summe der Abstandsquadrate minimal wird.
4. Wenn du glaubst, du hast nun die beste Gerade entdeckt, klicke auf das Kästchen bei „Trendlinie”. Die Trendlinie ist das Ergebnis der linearen Regression und gibt jene Gerade an, deren Abstandsquadrate minimal sind.
| Idee der Regression |
|---|
|
|
| Falls das Applet nicht angezeigt wird, klicke hier. |
Da wir im Unterricht die Regressionsgleichung immer mithilfe des Technologieeinsatzes lösen, überspringen wir die Herleitung der Regressionsgleichungen.
Regressionsgleichung mithilfe von Technologie berechnen und darstellen
| GeoGebra | Ti-8x |
|---|---|
| Wichtig beim ersten Mal: $\ $ Damit bei der Regression auch der Korrelationskoeffizient angezeigt wird, muss „Diagnostic“ auf „ON“ sein. Dies machst du, indem du auf Folgendes klickst:
$[2nd]+[0]$, dann gehe hinunter zu $DiagnosticOn$ und drücke $2$-mal $[Enter]$. Das Video zeigt dir, wie die Regression mit einer linearen Funktion funktioniert.
|
Lineare Regression
Bei der linearen Regression werden die Daten mithilfe einer linearen Funktion („Gerade“) verbunden.
Musterbeispiel
| Alter (X) | Gehalt (Y) |
|---|---|
| 25 | 1800 |
| 27 | 2500 |
| 28 | 2400 |
| 35 | 3000 |
| 40 | 3000 |
| 40 | 2000 |
| 50 | 3600 |
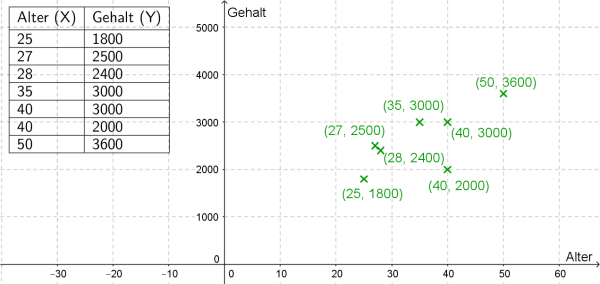
Gegeben ist die folgende Tabelle, die das Alter und Gehalt der Bediensteten in einer Firma angibt.
a) Stellen Sie die Daten in einer Punktwolke dar, wobei das Alter die $x$- und das Gehalt die $y$-Koordinate eines jeden Punktes angeben soll.
b) Ermitteln Sie die Gleichung der Regressionsgeraden und zeichnen Sie diese in die Graphik ein.
c) Berechnen Sie mithilfe der Gleichung der Regressionsgeraden jenes Gehalt, über das eine 45-jährige Person verfügen sollte.
d) Bestimmen Sie mithilfe der Gleichung der Regressionsgeraden jenes Alter, bei dem ein Gehalt von $€4 200$ erreicht werden sollte.
b) Ermitteln Sie die Gleichung der Regressionsgeraden und zeichnen Sie diese in die Graphik ein.
Durch Einsatz von Technologie erhalten wir die Gleichung $$f(x)=49.59x+878.63$$
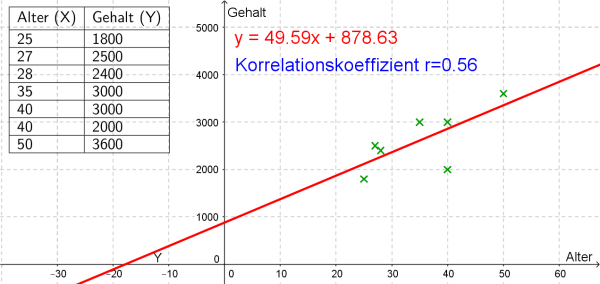
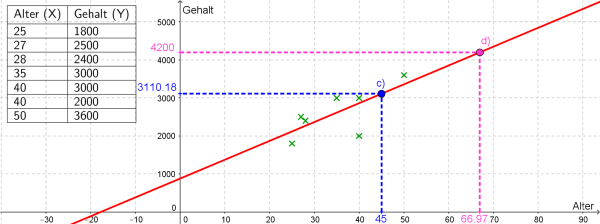
c) Berechnen Sie mithilfe der Gleichung der Regressionsgeraden jenes Gehalt, über das eine 45-jährige Person verfügen sollte.
Aus der Angabe wissen wir, dass $x=45$. Gesucht ist nun der passende $y$-Wert $y=f(45)$.
$$f(x)=49.59x+878.63$$
$$f(45)=49.59\cdot 45+878.63$$
$$f(45)=3110.18 $$
Bei einem Alter von 45 Jahren ist ein Gehalt von $€3 110.18$ zu erwarten.
d) Bestimmen Sie mithilfe der Gleichung der Regressionsgeraden jenes Alter, bei dem ein Gehalt von $€4 200$.
Gegeben ist die $y$-Korrdinate $y=f(x)=4200$. Gesucht ist nun der $x$-Wert:
$$f(x)=49.59x+878.63$$
$$4200=49.59x+878.63$$
Durch Freistellen von $x$ (siehe Äquivalenzumformungen) erhalten wir
$$x=66.97$$
Bei einem Alter von ca. $67$ Jahren wäre ein Gehalt von $€4 200$ zu erwarten (vorausgesetzt, die Person ist noch nicht in Pension).
Korrelationskoeffizient $r$
Durch Berechnung der Regressionsgeraden kann noch keine Aussage über die Stärke des Zusammenhangs zweier Merkmale ($X$ und $Y$) ausgesagt werden. Dazu benötigt man den
|
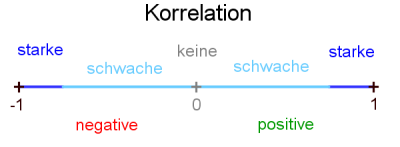
Korrelationskoeffizient $r$
Der Korrelationskoeffizient $r$ gibt an, wie stark zwei Merkmale $X$ und $Y$ zusammenhängen.
|
$Aha!$ $\ $ In folgendem GeoGebra-Applet lernst du, wie die Korrelation durch die Lage der Punkte verändert wird.
Wie dieses Applet funktioniert:
Verschiebe die grünen Punkte (Datenpunkte), so dass
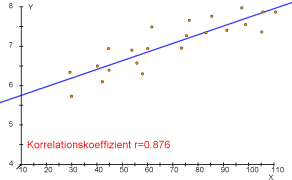
a) ein starker positiver Zusammenhang (d. h. $r\approx 1$),
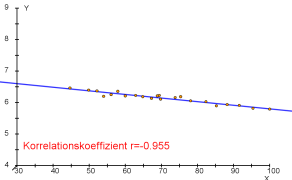
b) ein starker negativer Zusammenhang (d. h. $r\approx -1$),
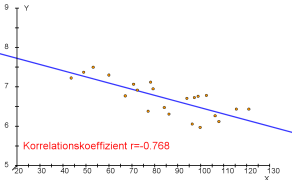
c) ein schwacher negativer Zusammenhang (d. h. $0.3\leq r\leq 0$) oder
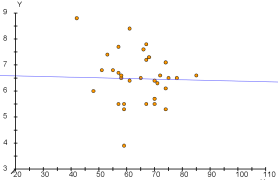
d) kein Zusammenhang (d. h. $r=0$)
herrscht.
| Übung zum Korrelationskoeffizient |
|---|
|
|
| Falls das Applet nicht angezeigt wird, klicke hier. |
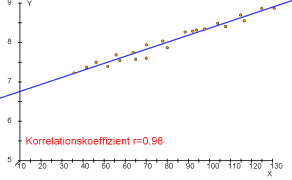
- Beispiele für Punktwolken und dazugehörende Korrelationskoeffizienten.
$r=-1$ (starke negative Korrelation)
$r=-0.77$ (starke negative Korrelation)
$r=-0.2$ (schwache negative Korrelation)
$r=0$ (keine Korrelation)
$r=0.8$ (starke positive Korrelation)
$r=0.98$ (starke positive Korrelation)
Liegen alle Punkte auf der Geraden, so ist $r=1$ oder $r=-1$, je nachdem ob der Zusammenhang positiv oder negativ ist.
Korrelation und Kausalität
|
Eine starke Korrelation (d. h. $\vert r\vert$ nahe bei 1) bedeutet noch lange nicht, dass es auch einen ursächlichen Zusammenhang zwischen zwei Merkmalen gibt. Oft spielen z. B. noch viel mehr Einflüsse eine Rolle. |
Beispiele für Korrelation aber (wahrscheinlich) keinen direkten ursächlichen Zusammenhang:
- Die Größe der Bevölkerung ($X$) hat Auswirkungen auf die Geschwindigkeit der Plattentektonik ($Y$).
- Je mehr Menschen auf einer Kontinentalplatte leben, desto schneller bewegt sich diese. Beispiele: Indien, Japan.
- Ein Rückgang an Störchen führt zu einer Abnahme an Neugeburten (Quelle).
- Tatsächlich spielt hier eine dritte Variable, nämlich die Verstädterung einer Region eine Rolle.
Matura-Aufgaben
|
Schrittfolge zur Berechnung von Regressionsaufgaben
|
$Bifie$: Schotterwerk (leicht-mittel-mittel)
siehe auch
$Bifie$: Reisekosten (leicht-leicht-schwer-leicht)
siehe auch
$Bifie$: Preis und Absatz (mittel)
siehe auch
$Bifie$: Hustensaft (mittel-mittel-leicht)
siehe auch
$Bifie$: Intelligenzquotient (leicht-leicht-leicht)
siehe auch
$Bifie$: Kängurusprünge (leicht-mittel-leicht)
siehe auch
$Bifie$: Elektronikhersteller (mittel-schwer-leicht)
siehe auch
$Bifie$: Sektkellerei (mittel-leicht-schwer)
siehe auch
$Bifie$: Fahrzeugtests (2) (mittel)
siehe auch
$Bifie$: CeBit (2) ((leicht-mittel-mittel)
siehe auch
$Bifie$: Jahresumsatz ((leicht-leicht-mittel)
siehe auch
$Bifie$: Kostenanalyse (leicht-mittel-leicht)
siehe auch
$Bifie$: Urlaubsreisen (mittel-leicht-leicht)
siehe auch
