Lineare Optimierung

Dieser Bereich ist nur für die HLW (Cluster 6) relevant.

Die lineare Optimierung eignet sich besonders für wirtschaftliche Anwendungen, um u. a. die optimale Produktionsmenge und den maximalen Gewinn zu bestimmen.

Inhaltsverzeichnis

1 Einleitung - Was ist lineare Optimierung?
2 Methode (zusammengefasst)
3 Video
4 Musterbeispiel
5 Übungs- und Maturaaufgaben

Einleitung - Was ist lineare Optimierung?

Im Jahre 1948 wurden beim Wiederaufbau der Stadt Moskau Mathematiker damit beauftragt, den Transport von Kies aus $20$ Kiesgruben zu $230$ Baustellen kostensparend zu optimieren. Mit Hilfe der linearen Optimierung konnte eine Kostensenkung von $10 %$ gegenüber dem ursprünglichen Preis erreicht werden. W. Knödl von der TU Wien errechnete 1960 mit Hilfe der linearen Optimierung einen optimalen Kostenplan für den Transport von Zucker aus fünf österreichischen Zuckerfabriken an alle $300$ österreichischen Großhändler. Auch hier konnten die Transportkosten um $10 %$ gesenkt werden. Heute wird die lineare Optimierung im Transportwesen angewendet, um Transportkosten zu senken, in der Landwirtschaft, um Nutzflächen optimal auszunützen, in der Organisationsplanung, um die günstigsten Stunden- und Schichtpläne zu ermitteln usw. Wir beschränken uns hier auf die Grundidee der linearen Optimierung und auf $2$ Variablen.

Methode (zusammengefasst)

Merke

$\ $

Lies zuerst den Text ganz genau durch und überlege dir, was gefragt ist. Was soll $x$ sein, was soll $y$ sein?
Dann werden aus der Angabe alle Nebenbedingungen in Form von Ungleichungen herausgelesen. Dazu gehören in der Regel auch immer die Nichtnegativitätsbedingungen.
Das Planungsfeld wird erstellt, indem die Lösungsmengen der Ungleichungen gezeichnet werden.
Die Zielfunktion wird aufgestellt: $Z$ gibt an, was maximiert/minimiert werden soll.
Der Graph der Zielfunktion wird in das Planungsfeld gezeichnet (mit $Z=0$) und anschließend bis zum optimalen Punkt parallel hinauf (für das Maximum) oder hinunter (für das Minimum) verschoben.
Die Koordinaten des optimalen Punktes werden bestimmt, indem man
a) die Koordinaten abliest

b) den Schnittpunkt der beiden Geraden, die sich in diesem Punkt schneiden, berechnet.

Bemerkungen:

Meistens gibt es nur einen Lösungspunkt. Es kann aber auch vorkommen, dass die Zielfunktion zu einer Begrenzungsgeraden parallel ist und hier auch optimal ist. Jeder Punkt der Geraden, der auch im Planungsfeld liegt, ist dann Lösungspunkt.
Die hier beschriebene graphische Lösungsmethode ist nur für zwei (höchstens drei) Variablen anwendbar. In der Praxis treten viel mehr Variablen auf; solche Verfahren sind nur noch mit rechnerischen Methoden (z. B. Simplex-Algorithmus) zu bewältigen.
Hauptsatz der linearen Optimierung: Die Zielfunktion erreicht ihr Maximum oder Minimum stets am Rand des zulässigen Bereichs. In den meisten Aufgabenstellungen ist die Lösung eindeutig und liegt in einem Eckpunkt des zulässigen Bereichs.

Video

Aufstellen der Nebenbedingungen und Zielfunktion	Planungsfeld und optimaler Punkt

Musterbeispiel

Eine Kleiderfabrik stellt Hosen und Röcke her. Täglich kann man $70$ Hosen und $100$ Röcke nähen, allerdings insgesamt nicht mehr als $140$ Stück. Die Herstellungskosten betragen $20€$ für eine Hose und $15€$ für einen Rock. Der Verkaufspreis je Hose beträgt $45€$ und je Rock $35€$.

a) Übersetze die Nebenbedingungen aus dem Text in Ungleichungen.
b) Stelle die Zielfunktion auf, wobei maximaler Gewinn angestrebt werden soll.
c) Löse das System und interpretiere die Lösung.

Lösung

a) Übersetze die Nebenbedingungen aus dem Text in Ungleichungen.

Sei $x$ die Anzahl der Hosen, $y$ die Anzahl der Röcke.

„Täglich kann man $70$ Hosen und $100$ Röcke nähen“

$$ I:x\leq 70$$ $$II: y\leq 100 $$

„allerdings insgesamt nicht mehr als $140$ Stück“

$$ III: x+y\leq 140 \rightarrow y\leq -x+140 $$ Nichtnegativitätsbedingungen: $$ IV: x\geq 0 \textrm{ und }V: y\geq 0$$

b) Stelle die Zielfunktion auf, wobei maximaler Gewinn angestrebt werden soll.

„Die Herstellungskosten betragen $20€$ für eine Hose und $15€$ für einen Rock. Der Verkaufspreis je Hose beträgt $45€$ und je Rock $35€$.“

Gewinn für eine Hose: $45€-20€=25€$.
Gewinn für einen Rock: $35€-15€=20€$.
Somit lautet die Zielfunktion, die den Gewinn angibt:

$$\begin{align} Z=25x+20y &\rightarrow -25x+Z=20y \\ &\rightarrow y=-\frac{25}{20}x+\frac{Z}{20} \end{align}$$

c) Löse das System und interpretiere die Lösung.

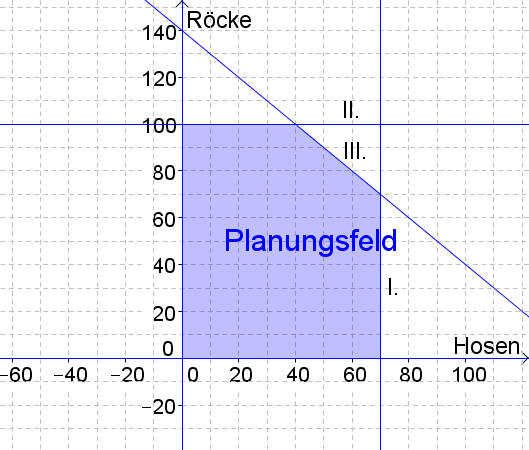
1. Schritt: Zuerst zeichnen wir das Planungsfeld:

$\begin{align} I:&x\leq 70&\\ II:&y\leq 100&\\ III: &x+y\leq 140& \rightarrow y\leq -x+140 \\ IV:& x\geq 0&\\ V: &y\geq 0& \end{align}$

2. Schritt: Dann zeichnen wir die Zielfunktion ein und verschieben sie parallel ganz nach oben, bis sie das Planungsfeld nur noch in einem Punkt berührt.

$$y=-\frac{25}{20}x+\frac{Z}{20}\rightarrow k=\frac{25}{20} \textrm{und $d$ kann frei gewählt werden.}$$

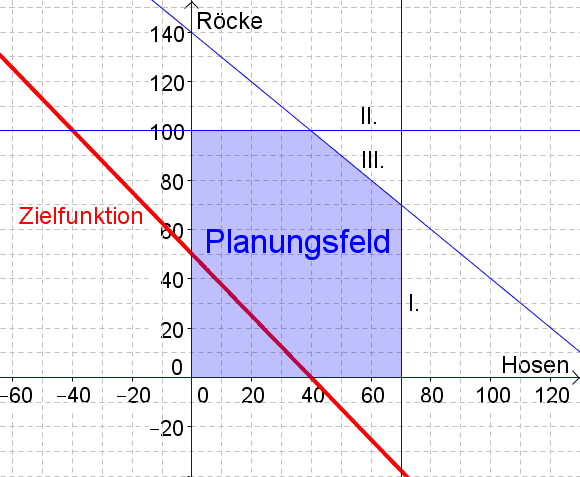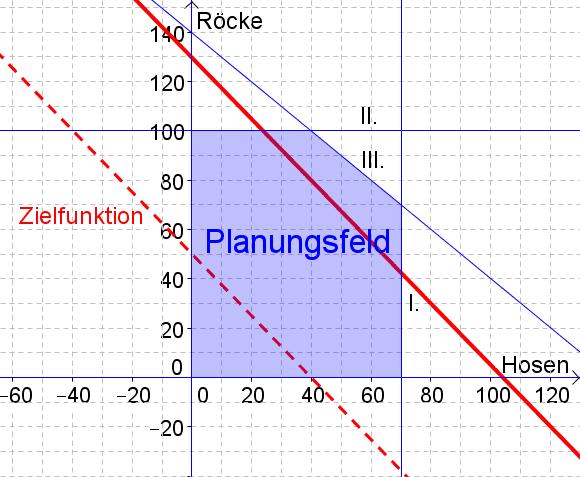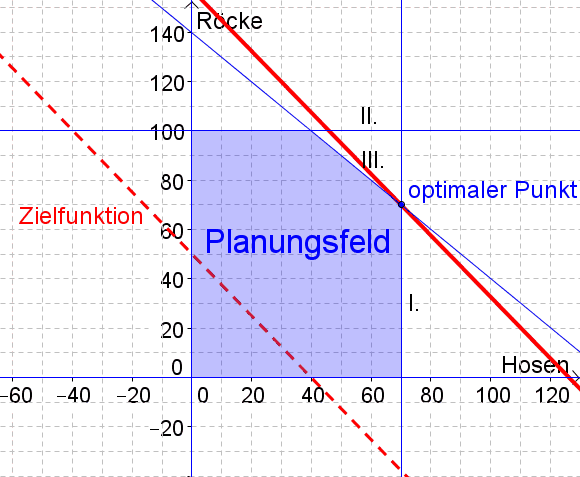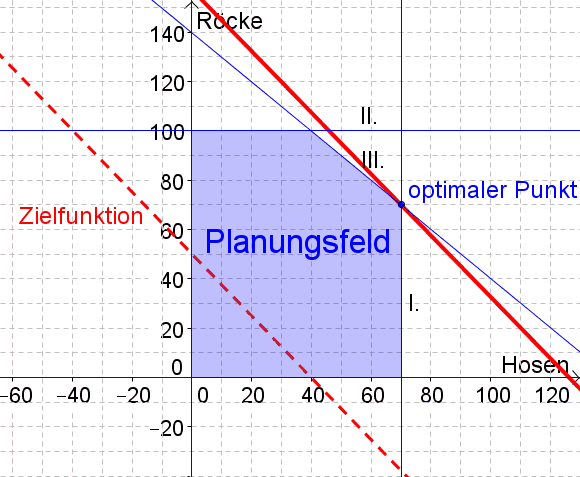
Die Zielfunktion zeichnest du ein, wenn du für k 20 nach rechts und 25 hinunter gehst.

Der optimale Punkt ist der Schnittpunkt von $I: x=70$ und $II: y=-x+140$. (Hinweis: Natürlich können die Koordinaten des optimalen Punktes auch abgelesen werden, wir wollen sie hier aber berechnen).

3. Schritt Nun berechnen wir den optimal Punkt, indem wir die Geraden $I: x=70$ und $III: y=-x+140$ schneiden:

$$I: x=70$$ $$III: y=-x+140$$ Einsetzungsverfahren: I in III einsetzen. $$ y=-70+140 \rightarrow y=70$$ Somit lauten die Koordinaten des optimalen Punktes: $P(70|70)$

4. Schritt: Zuletzt berechnen wir noch den maximalen Gewinn, indem wir den optimalen Punkt $(70|70)$ in die Zielfunktion $Z=25x+20y$ einsetzen: $$Z=25\cdot 70+20\cdot 70=3150$$

5. Schritt: Antwortsatz Der maximale Gewinn von $3150€$ wird bei einer Produktion von $70$ Hosen und $70$ Röcken erzielt.