Wahrscheinlichkeit: Normalverteilung und Stetige Zufallsvariablen

Grundbegriffe für stetige Zufallsvariablen
Normalverteilung
Übungs- und Maturaaufgaben

Nun beschäftigen wir uns mit Zufallsvariablen, die jeden Wert in einem bestimmten reellen Intervall annehmen können, z. B. alle Werte zwischen $2.5$ und $10$. Dies sind sogenannte stetige Zufallsvariablen. Beispiele für stetige Zufallsvariablen sind die Körpergröße oder das Gewicht eines Menschen, die Lebensdauer eines Bauteils, die Wartedauer in einer Schlange usw.

Dichtefunktion

Anstelle der Wahrscheinlichkeitsfunktion $P$ für diskrete Zufallsvariablen, definiert man für stetige Zufallsvariablen die Dichtefunktion $f$.

Definition

Die Dichtefunktion $f$ ist eine Funktion mit den Eigenschaften:

Die Funktionswerte von $f$ sind immer positiv

$$f(x)\geq 0 $$ und

die Fläche unterhalb der Dichtefunktion ist $1$

$$\int_{-\infty}^{+\infty} f(x)\cdot dx=1$$

Der Grund, warum man nicht die Wahrscheinlichkeitsfunktion $P$ verwendet, liegt darin, dass stetige Zufallsvariablen unendlich viele (überabzählbar viele) Werte haben und die Wahrscheinlichkeit, dass ein ganz bestimmter Wert auftritt, gleich $0$ ist (Begründung siehe unten).

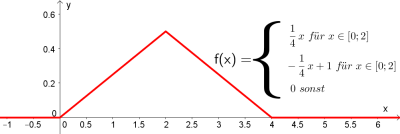
1. Beispiel einer Dichtefunktion	2. Beispiel einer Dichtefunktion

$$f(x)\geq 0$$ und $$\int_{-\infty}^{\infty} f(x)\cdot dx=\int_{0}^{4} \frac{1}{4}=1$$	$$f(x)\geq 0 $$ und $$\int_{-\infty}^{\infty} f(x)\cdot dx=\int_{0}^{2} \frac{1}{4}x\cdot dx + \int_{2}^{4} -\frac{1}{4}x\cdot dx=\frac{1}{2}+\frac{1}{2}=1$$

Verteilungsfunktion

Mithilfe der Dichtefunktion definieren wir nun (ähnlich wie bei den diskreten Zufallsvariablen) die ...

Die Fläche kann als Wahrscheinlichkeit interpretiert werden: $$P(X\leq 2.5)=\int_{-\infty}^{2.5} f(x)\cdot dx=0.72$$

Definition

Verteilungsfunktion $F$

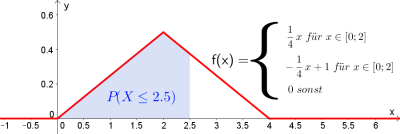
$$F(x)=P(X\leq x)= \int_{-\infty}^{x} f(t)\cdot dt$$ Sie gibt die Wahrscheinlichkeit an, dass $X$ einen Wert $\leq x$ annimmt.

Wichtig: Die Funktionswerte der Dichtefunktion $f(x)$ geben NICHT die Wahrscheinlichkeit $P(X=x)$ an. Bei stetigen Zufallsvariablen können wir nur die Wahrscheinlichkeit dafür angeben, dass die Zufallsvariable $X$ Werte in einem bestimmten Intervall annimmt.

$$P(1\leq X\leq 2.5)=\int_{1}^{2.5} f(x)\cdot dx=0.65$$

Merke

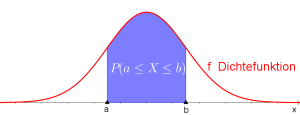
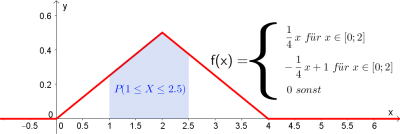
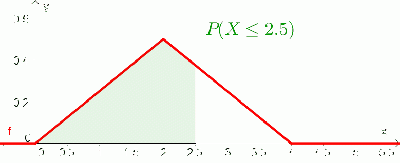
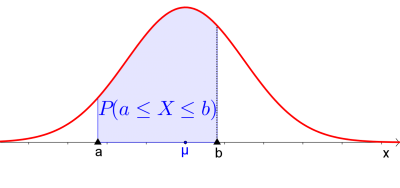
Die Wahrscheinlichkeit, dass die stetige Zufallsvariable $X$ einen Wert im Intervall $[a;b]$ annimmt, entspricht der Fläche unter der Dichtefunktion zwischen den Grenzen $a$ und $b$:

$$P(a\leq X\leq b)= \int_{a}^{b} f(x)\cdot dx = F(b)-F(a)$$

Hinweis:

Die Wahrscheinlichkeit, dass $X$ einen bestimmten Wert $a$ annimmt ist $0$, da:

$$P(a\leq X\leq a)= \int_{a}^{a} f(x)\cdot dx = F(a)-F(a)=0$$

$P(X\leq a)=P(X<a)$

Begründung: $ P(X\leq a)=P(X<a)+P(X=a)$ und da $P(X=a)=0$ ist, folgt die Behauptung.

$P(a\leq X\leq b)=P(X\leq b)-P(X\leq a)$, wie aus der rechten Skizze leicht zu sehen ist.

Erwartungswert und Standardabweichung

Definition

Für stetige Zufallsvariablen sind Erwartungswert $\mu$ und Standardabweichung $\sigma$ wie folgt definiert:

$$E(x)=\mu=\int_{-\infty}^{+\infty} x\cdot f(x)\cdot dx$$ $$\sigma =\sqrt{\int_{-\infty}^{+\infty} (x-\mu)^2 f(x)\cdot dx}$$

Berechnen Sie Erwartungswert und Standardabweichung der folgenden zwei Dichtefunktionen. Erklären Sie die Gemeinsamkeiten bzw. Unterschiede bei $\mu$ und $\sigma$:

1. Dichtefunktion	2. Dichtefunktion

	1. Dichtefunktion	2. Dichtefunktion
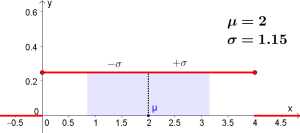
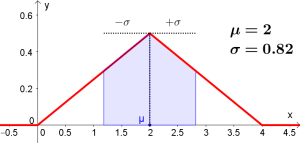
$\mu$	$$\mu=\int_{-\infty}^{\infty} x\cdot f(x)\cdot dx=\int_{0}^{4} \frac{1}{4}x=\frac{1}{4}\cdot \frac{x^2}{2}\vert _{0}^{4}=2$$ $$\mu = 2$$	$$\mu=\int_{-\infty}^{\infty} f(x)\cdot dx=\int_{0}^{2} \underbrace{x \cdot \frac{1}{4}x}_{-\frac{1}{4}x^2}+\int_{2}^{4} \underbrace{x\cdot (-\frac{1}{4}x+1)}_{ -\frac{1}{4}x^2+x}=$$ $$=\frac{1}{4}\cdot\frac{x^3}{3}\vert_{0}^{2} +[-\frac{1}{4}\cdot\frac{x^3}{3}+\frac{x^2}{2}]_{2}^{4}=$$ $$=\frac{1}{4}\cdot\frac{2^3}{3}-0 +\left[-\frac{1}{4}\cdot\frac{4^3}{3}+\frac{4^2}{2}-(-\frac{1}{4}\cdot\frac{2^3}{3}+\frac{2^2}{2})\right]=$$ $$=\frac{2}{3}+\left[-\frac{16}{3}+8-(-\frac{2}{3}+2)\right]=2$$
$\sigma$	$$\sigma=\sqrt{\int_{-\infty}^{\infty} (x-\mu )^2 \cdot f(x)\cdot dx}=$$ $$=\sqrt{\int_{0}^{4} \underbrace{(x-2)^2}_{x^2-4x+4}\cdot \frac{1}{4}\cdot dx }=$$ $$=\sqrt { \frac{1}{4} \left( \frac{x^3}{3} - \frac{4x^2}{2}+4x \right) \vert_{0}^{4} }=$$ $$=\sqrt{\frac{1}{4}\cdot (\frac{4^3}{3}-\frac{4^3}{2}+16)}=\frac{2}{\sqrt{3}}\approx 1.15$$	$$\sigma=\sqrt{\int_{-\infty}^{\infty} (x-\mu )^2 \cdot f(x)\cdot dx}$$ $$=\sqrt{\int_{0}^{2}(x-2)^2\cdot \frac{1}{4}\cdot x + \int_{2}^{4}(x-2)^2\cdot (-\frac{1}{4}\cdot x+1)}=...$$ $$\sigma=\frac{\sqrt{6}}{3}\approx 0.82$$
Graph	1. Dichtefunktion. Eingezeichnet ist der Erwartungswert $\mu$ und die sogenannte $\sigma$-Umgebung.	1. Dichtefunktion. Eingezeichnet ist der Erwartungswert $\mu$ und die sogenannte $\sigma$-Umgebung.

Wichtig: Während beide Zufallsvariablen über denselben Erwartungswert verfügen ($\mu=2$), unterscheiden sie sich in ihrer Standardabweichung. Die Zufallsvariable mit der Dichtefunktion 1 weist eine höhere Streuung auf als jene Zufallsvariable mit der Dichtefunktion 2.

Eine der wichtigsten stetigen Verteilungsfunktionen ist die Normalverteilung (siehe nächste Seite).

$\rightarrow$ nächste Seite ...

Inhaltsverzeichnis

1 Einleitung
2 $\sigma$-Umgebungen
3 Binomial- und Normalverteilung
4 Verteilungsfunktion einer Normalverteilung
5 Übungsbeispiele

Einleitung

Dichtefunktion einer $N(\mu ;\sigma )$-verteilten Zufallsvariable.

Definition

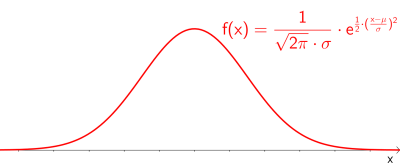
Eine stetige Zufallsvariable ist normalverteilt mit Erwartungswert $\mu$ und Standardabweichung $\sigma$ (kurz: $N(\mu ;\sigma)$-verteilt), wenn für die Dichtefunktion $f$ gilt:

$$ f(x)=\frac{1}{\sqrt{2\pi}\cdot \sigma}\cdot e^{\frac{1}{2}\cdot (\frac{x-\mu}{\sigma})^2}$$

Die Dichtefunktion der Normalverteilung wird aufgrund ihrer Form „Gaußsche Glockenkurve“ genannt.

Eigenschaften des Graphen der Dichtefunktion :

Die Glockenkurve ist symmetrisch zum Erwartungswert $\mu$, bei dem sie auch ihren einzigen Hochpunkt hat.
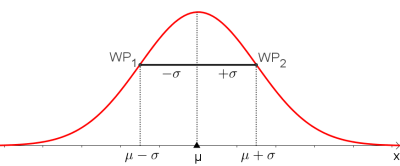
Die beiden Wendepunkte der Glockenkurve befinden sich bei $\mu -\sigma$ und $\mu +\sigma$.
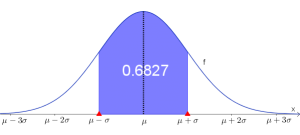
Im Intervall $[\mu -\sigma ; \mu -\sigma]$ befinden sich ca. $68 \%$ aller Werte.
Die Glockenkurve nähert sich asymptotisch der $x$-Achse an und es gilt

$$\lim_{x\rightarrow \pm \infty} f(x) =0$$

Die Dichtefunktion erfüllt alle wichtigen Eigenschaften einer Dichtefunktion:

$f(x)\geq 0$ und

$\int_{-\infty}^{+\infty} f(x)\cdot dx=1$ (d. h. die Fläche unterhalb der Dichtefunktion ist $1$).

Die Normalverteilung ist deshalb so wichtig, da es in der Natur und im Alltag sehr viele Zufallsvariablen gibt, die eine solche Verteilung aufweisen und somit eine Dichtefunktion besitzen, deren Graph glockenförmig ist.

Merke

Die Berechnung von Wahrscheinlichkeiten erfolgt über die Berechnung der Fläche unterhalb der Dichtefunktion.

Für die Verteilungsfunktion $F$ gilt wieder: $$F(x)=P(X\leq x)=\int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}\cdot \sigma}\cdot e^{\frac{1}{2}\cdot (\frac{t-\mu}{\sigma})^2}\cdot dt$$

Die Berechnung dieses Integrals erfolgt in der Regel mithilfe des Taschenrechners bzw. mit GeoGebra.

Das folgende Applet von Lindner zeigt dir die wichtigsten Eigenschaften der Glockenkurve:

Verschiebung der Normalverteilung

Falls dieses Applet nicht funktioniert: Klicke hier

Merke

$\\ $

Ändert sich der Erwartungswert $\mu$, so wandert die Glockenkurve nach links oder rechts.
Ändert sich die Standardabweichung $\sigma$, so ändern sich zwei Sachen:

a) die Glockenkurve wird breiter (bei zunehmender Standardabweichung) bzw. schmaler (bei abnehmender Standardabweichung).

b) die Glockenkurve wird flacher bzw. höher, da die Fläche unter der Kurve $1$ bleiben muss.

Wichtige Überlegungen:

$$P(X\leq \mu)=0.5$$

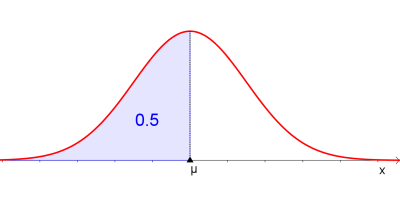
$P(X\leq \mu)=0.5$

$$P(X\leq b)$$

$P(X\leq b)=F(b)$

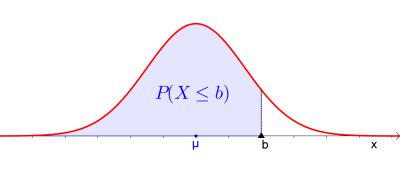
$$ P(X \geq b)=1-P(X \leq b)$$

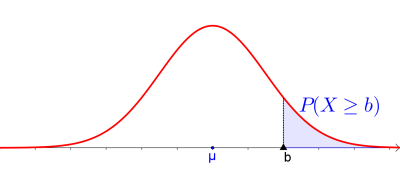
$P(X\geq b)=1-P(X\leq b)$

$$ P(a\leq X\leq b)$$

$P(a\leq X\leq b)=P(X\leq b)-P(X\leq a)$

Zur Wiederholung und Erheiterung ein Video vom berühmten "DorFuchs" zur Normalverteilung und seinem IQ:

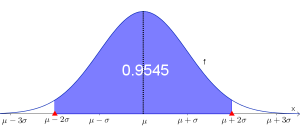
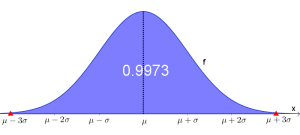
$\sigma$-Umgebungen

Für jede normalverteilte Zufallsvariable $X$ gilt, dass die $\sigma$-Bereiche um den Erwartungswert $\mu$ eine konstante Fläche beinhalten.

$P(\mu-\sigma\leq X\leq \mu +\sigma)\approx 68.3\%$

$P(\mu-2\sigma\leq X\leq \mu +2\sigma)\approx 95.4\%$

$P(\mu-3\sigma\leq X\leq \mu +3\sigma)\approx 99.73\%$

Binomial- und Normalverteilung

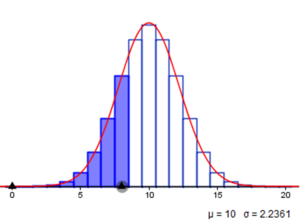
Die Binomialverteilung kann durch die Normalverteilung angenähert werden. Graphisch ist dies gut erkennbar: Je symmetrischer die Wahrscheinlichkeitsfunktion der Binomialverteilung ist und umso größer der Stichprobenumfang $n$ (d. h. die Anzahl der Balken), desto ähnlicher wird die Wahrscheinlichkeitsfunktion der Binomialverteilung der Glockenkurve der Normalverteilung.

Die Graphik zeigt das Histogramm einer binomialverteilten Zufallsvariablen mit $n=20$ und $p =0.5$. Die blauen Balken visualisieren die Wahrscheinlichkeit $P(0≤X≤8)$, die rote Kurve stellt die Normalapproximation dar. Die Fläche unter der Kurve im Intervall $(-\infty, 8]$ entspricht näherungsweise der Gesamtfläche der blauen Balken.

Merke

Die Binomialverteilung darf näherungsweise durch die Normalverteilung ersetzt werden, wenn die Bedingung

$$n\cdot p\cdot (1-p)>9$$ erfüllt ist.

Verteilungsfunktion einer Normalverteilung

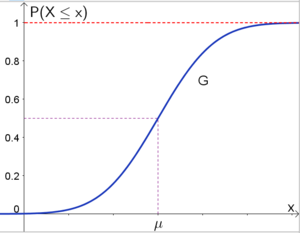
Graph der Verteilungsfunktion einer normalverteilten Zufallsvariable $X$

Wir haben oben schon gelernt, dass die Wahrscheinlichkeit der Fläche unter der Dichtefunktion entspricht. Sei $f$ die Dichtefunktion einer normalverteilten Zufallsvariable $X$. Dann gilt für die Wahrscheinlichkeit $P(X\leq x)$ (d. h. die Wahrscheinlichkeit, dass die Zufallsvariable $X$ einen Wert kleiner oder gleich $x$ annimmt):$$P(X\leq x)=\int_{-\infty}^{x} f(x)\cdot dx$$

Dieses Integral können wir nun als Funktion interpretieren, die uns für jedes $x$ die Fläche unter der Glockenkurve links von $x$ angibt. D. h.: $$G(x)=\int_{-\infty}^{x} f(x)\cdot dx$$

Definition

Die Verteilungsfunktion $G$ mit

$$G(X)=P(X\leq x)=\int_{-\infty}^{x} f(x)\cdot dx$$ gibt die Wahrscheinlichkeit $P(X\leq x)$ für einen beliebigen Wert $x$ an.

Das folgende Applet zeigt dir die Graphen der Dichtefunktion (links) und der Verteilungsfunktion (rechts) an.

Merke

$\\ $

Die Verteilungsfunktion ist streng monoton steigend.
Die Verteilungsfunktion konvergiert gegen den Wert $1$, da auch die Fläche unter der Glockenkurve gegen $1$ konvergiert.
Bei $\mu$ hat die Verteilungsfunktion immer den Wert $0.5$, da $P(x\leq \mu)=0.5$.

Übungsbeispiele

In einer Fabrik wird Senf in Gläser zu $250 g$ verpackt. Vom Hersteller der Füllmaschine wird der Senffabrik nahegelegt, den Sollwert (Mittelwert $\mu$) auf $265 g$ einzustellen. Dabei ergibt sich eine mittlere Abweichung $\sigma=10 g$.

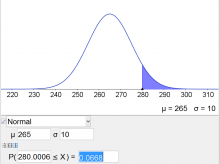
a) Wahrscheinlichkeit rechts von $\mu$ berechnen: Wie viele Gläser enthalten mehr als $280 g$ Senf?

Die Variable $X$ ist $N(265;10)$-verteilt und gibt die Füllmenge in Gramm (g) an.

GeoGebra / Graph	Ti-8X	Per Hand / Tabelle
Gesucht ist $P(X> 280)$	$$P(X>280)=1-P(X\leq 280)=$$ $$=1-normcdf(-\infty,280,265,10)=$$ $$=0.06681$$	$$P(X>280)=1-P(X\leq 280)=$$ $$=\underbrace{P(X\leq 265 + 1.5\cdot 10)}_{P(X\leq \mu + z\cdot \sigma)}=$$ $$=1-\Phi (1.5)=$$ $$=1-0,93319=0.06681$$

Die Wahrscheinlichkeit $P(X> 280g)$ beträgt $6.681\%$.

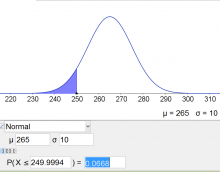
b) Wahrscheinlichkeit links von $\mu$ berechnen: Berechnen Sie die Wahrscheinlichkeit, dass ein Glas weniger als $250 g$ enthält?

GeoGebra / Graph	Ti-8X	Per Hand / Tabelle
Gesucht ist $P(X< 250)$	$$P(X<250)=$$ $$=normcdf(-\infty,250,265,10)=$$ $$=0.06681$$	$$P(X<250)=P(X<265-15)$$ $$=\underbrace{P(X\leq 265 - 1.5\cdot 10)}_{P(X\leq \mu - z\cdot \sigma)}=$$ $$=\Phi (-1.5)=1-\Phi (1.5)$$ $$=1-0,93319=0.06681 $$

Die Wahrscheinlichkeit $P(X<250g)$ beträgt ebenfalls $6.681\%$. Auf dieses Ergebnis hätten wir auch einfacher kommen können, da $280g$ und $250g$ gleich weit von $\mu=265g$ entfernt sind und aufgrund der Symmetrie der Normalverteilung erhalten wir dasselbe Ergebnis.

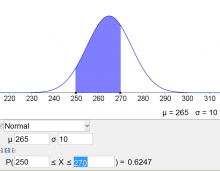
c) Wahrscheinlichkeit in einem bestimmten Bereich: Wie groß ist die Wahrscheinlichkeit, dass ein Glas zwischen $250 g$ und $270 g$ enthält?

GeoGebra / Graph	Ti-8X	Per Hand / Tabelle
Gesucht ist $P(250\leq X\leq 270)$	$$P(250\leq X\leq 270)=P(X\leq 270)-P(X\leq 250)$$ $$=normcdf(-\infty,270,265,10)-normcdf(-\infty,250,265,10)=$$ $$=0.6247$$	$$P(250\leq X\leq 270)=P(X\leq 270)-P(X\leq 250)$$ $$=\underbrace{P(X\leq 265 + 0.5\cdot 10)}_{P(X\leq \mu + z\cdot \sigma)}-\underbrace{P(X\leq 265 - 1.5\cdot 10)}_{P(X\leq \mu + z\cdot \sigma)}=$$ $$=\Phi (0.5)-\Phi(-1.5)=$$ $$=\Phi (0.5)-(1-\Phi(1.5))$$ $$ 0.69146 -0.06681=0.6247$$

Die Wahrscheinlichkeit $P(250g\leq X\leq 270g)$ beträgt $62.47\%$.

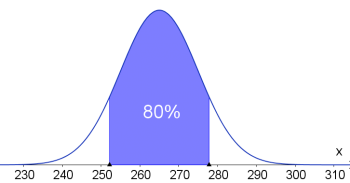
d) Ermitteln eines symmetrischen Intervalls um $\mu$: In welchem symmetrischen Bereich um den Mittelwert liegen $80\%$ der Gläser?

Hier wird jetzt die Umkehrung gebraucht. Die Wahrscheinlichkeit ist bekannt und die $x$-Werte sind gesucht (vorher war es immer umgekehrt).

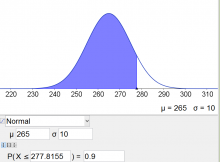
Gesucht ist $P(\mu -k \leq X\leq \mu + k)=0.8$ (siehe Grafik) Somit müssen zwischen $\mu$ und $\mu +k$ insgesamt $40\%$ aller Werte liegen ($40\%$ sind links und $40\%$ sind rechts von $\mu$ ). Insgesamt liegen dann $50+40=90\%$ links von $\mu+k$ (d. h. $P(X\leq \mu+k)=0.9$). Mit dieser Überlegung können wir nun $k$ bestimmen:

GeoGebra / Graph

Ti-8X

Per Hand / Tabelle

$P(X\leq \mu+k)=0.9\rightarrow \mu+k=277.82\rightarrow k=12.82$

Somit ist das gesuchte Intervall: $$[\mu -k ; \mu + k]=[252.18;277.82]$$

Alternativer CAS-Befehl: $$Normal[265, 10, 265+x]-Normal[265, 10, 265-x]=0.8$$ $$\rightarrow x=12.82$$

$$P(X\leq \mu+k)=0.9$$

$$\rightarrow \mu+k=invNorm(0.9,265,10)$$ $$\mu+k=277.82\rightarrow k=12.82$$ Somit ist das gesuchte Intervall: $$[\mu -k ; \mu + k]=[252.18;277.82]$$

$$P(\mu-z\cdot \sigma \leq X\leq \mu+z\cdot \sigma)=0.8$$

$$P(X\leq \mu+z\cdot \sigma)-P(X\leq \mu-z\cdot \sigma)=0.8$$ $$\Phi (z)-\Phi(-z)=0.8$$ $$\Phi (z)-(1-\Phi (z))=0.8$$ $$2\cdot \Phi (z)-1=0.8$$ $$\Phi (z) =\frac{1+0.8}{2}=0.9$$ $$\rightarrow z\approx 1.28$$ $\mu+z\cdot \sigma=265+1.28\dot 10=277.8$ und $\mu-z\cdot \sigma=265-1.28\dot 10=252.2$

Somit ist das gesuchte Intervall: $$[\mu -k ; \mu + k]=[252.18;277.82]$$

Im symmetrischen Intervall $[252.18g;277.82g]$ liegen $80\%$ der Gläser.

e) Ermitteln von $\mu$ bei bekannter Wahrscheinlichkeit: Welchen Mittelwert $\mu$ könnte die Senffirma einstellen, wenn sie $10\%$ untergewichtigen Ausschuss toleriert?

$\mu=$? und $\sigma=10$. Gesucht ist, für welches $\mu$ gilt $P(X\leq 250)=0.10$.

GeoGebra	Ti-8X	Per Hand / Tabelle
Dies berechnet man am besten mithilfe des CAS: $$Normal[\mu, 10, 250]=0.1\rightarrow \mu=262.82$$	Dies berechnet man am besten mithilfe des Solve-Befehls: $$normalcdf(-\infty,250,x, 10)=0.1$$ $$\rightarrow 0=normalcdf(-\infty,250,x, 10)-0.1$$ $$\rightarrow \mu=262.82$$	$$P(X\leq 250)=0.10$$ $$P(X\leq \underbrace{\mu+z\cdot 10}_{=250} )=0.10$$ $$\Phi (z)=0.1\rightarrow z\approx -1.28$$ $$ 250=\mu+(-1.29)\cdot 10 \rightarrow \mu=262.8$$

Der Mittelwert könnte auf $262.8g$ eingestellt werden.