Trigonometrie

Was lernst du hier?
Grundwissen - Das rechtwinklige Dreieck
Vermessungsaufgaben
Vertiefung: Betrachtungen im Einheitskreis
Trigonometrische Funktionen
Das allgemeine Dreieck - Sinussatz und Cosinussatz
Formelsammlung
Beispiele

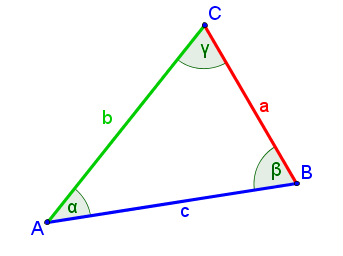
In der Trigonometrie beschäftigen wir uns mit Dreiecken (Tri-gono-metrie = Drei-ecks-messung)

Die folgende Seite ist in $5$ Theorieabschnitte gegliedert, die das Lernen erleichtern sollen:

Grundwissen - Das rechtwinklige Dreieck: Hier lernst du die Grundbegriffe und Grundrechnungen im rechtwinkligen Dreieck kennen.
Vermessungsaufgaben, in denen du das zuvor Gelernte in Anwendungsbeispielen verwenden kannst.
Vertiefung: Betrachtungen im Einheitskreis: In diesem Abschnitt lernst du das Bogenmaß und den Einheitskreis kennen.
Trigonometrische Funktionen: Hier lernst du die typischen Graphen der Sinus-, Cosinus- und Tangensfunktion kennen.
Das allgemeine Dreieck, indem du lernst, in Dreiecken, die keinen rechten Winkel haben, mit dem Sinus- und dem Cosinussatz zu rechnen.

Die letzten beiden Kapitel bestehen aus einer Zusammenfassung der hier verwendeten Formeln und Matura-Aufgaben.

$\rightarrow$ nächste Seite ...

Begriffe

rechtwinkliges Dreieck

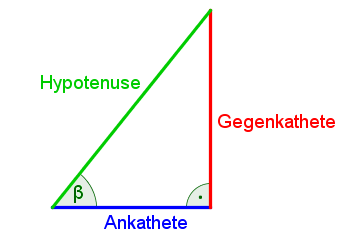
Gegeben ist ein rechtwinkliges Dreieck ($=$ Dreieck mit einem $90°$-Winkel).

Die längste Seite im rechtwinkligen Dreieck heißt Hypotenuse. Sie ist IMMER gegenüber vom rechten Winkel.

Die beiden kürzeren Seiten heißen Katheten. Ausgehend vom Winkel $\beta$ (siehe Skizze) können die beiden Katheten folgendermaßen unterschieden werden:

* Die Gegenkathete GK liegt $\beta$ gegenüber.

* Die Ankathete AK liegt an $\beta$ an.

Wichtig: Beachte, dass es immer vom ausgehenden Winkel abhängt, welche Kathete die Gegenkathete (gegenüber dem Winkel) und welche Kathete die Ankathete (dem Winkel anliegend) ist!

Sinus, Cosinus und Tangens

Definition

Der Sinus eines Winkels $\alpha$ ist definiert als das Verhältnis von GK zu H:	$\ \mathbf{sin\ \alpha = \frac{GK}{H}}$
Der Cosinus eines Winkels $\alpha$ ist definiert als das Verhältnis von AK zu H:	$\ \mathbf{cos\ \alpha = \frac{AK}{H}}$
Der Tangens eines Winkels $\alpha$ ist definiert als das Verhältnis von GK zu AK:	$\ \mathbf{tan\ \alpha = \frac{GK}{AK}}$

$Aha!$ Das folgende Arbeitsblatt zeigt dir, dass diese Verhältnisse (Sinus, Cosinus und Tangens) nur vom Winkel abhängen, nicht aber von der Größe des Dreiecks.

Sollte das Arbeitsblatt nicht funktionieren, klicke hier.

Wichtig: Sinus, Cosinus und Tangens gelten nur im rechtwinkligen Dreieck.

Steigung und Steigungswinkel

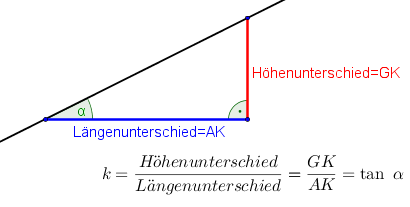
Aus dem Kapitel Lineare Funktionen wissen wir bereits, dass $k=\frac{Höhenunterschied}{Längenunterschied}$ die Steigung angibt. Betrachtet man die folgende Skizze, so kann folgender Zusammenhang festgestellt werden:

$$k=\frac{Höhenunterschied}{Längenunterschied}=\frac{GK}{AK}=\tan \alpha$$ Somit erhalten wir die Formel:

$$k=\tan \alpha$$

Mit dieser Formel kann nun einfach zwischen der (prozentuellen) Steigung und dem Steigungswinkel gewechselt werden:

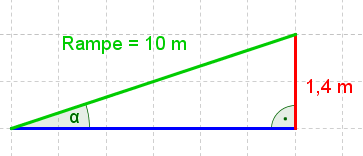
Eine $10 m$ lange Rampe legt einen Höhenunterschied von $1.4 m$ zurück.
- Fertigen Sie eine Skizze und zeichnen Sie die angegebenen Größen ein.
- Bestimmen Sie
$\qquad \qquad \quad$ a) den Steigungswinkel.
$\qquad \qquad \quad$ b) die prozentuelle Steigung.

Skizze der Rampe

a) Berechnung des Steigungswinkels:

$\sin\ \alpha = \frac{GK}{H}=\frac{1.4}{10}\ \ \ \ \vert $ im TR: $sin^{-1}$

$\alpha = 8.05°$

b) Mithilfe der Formel $k=\tan \alpha$ können wir die prozentuelle Steigung auch ohne den Längenunterschied (in der Skizze die blaue Strecke) berechnen: $$k=\ tan\ \alpha$$ $$k=\tan \ 8.05°$$ $$k=0.14=14 \%$$ A: Die Steigung beträgt $14 \%$.

Übungen im rechtwinkligen Dreieck

? : Online-Übungen zur Überprüfung, ob die richtige Formel verwendet wurde

? : Weitere Übungen zur Überprüfung der Formel

? : Und noch eine Übung dazu

Rechenbeispiele von Jutta Gut (mit Lösungen)

Aufgabenblatt mit Textaufgaben (mit Lösungen)

$\rightarrow$ nächste Seite ...

Vermessungsaufgaben

Begriffe

Blick des Auges (links) auf ein Objekt

Höhenwinkel

Der Höhenwinkel ist der Winkel zwischen der Horizontalen ($=$ waagrechte Gerade) und „dem Blick in die Höhe“.

Tiefenwinkel

Der Tiefenwinkel ist der Winkel zwischen der Horizontalen ($=$ waagrechte Gerade) und „dem Blick in die Tiefe“.

Sehwinkel

Der Sehwinkel ist jener Winkel, der das Objekt (in der rechten Abbildung die senkrechte Strecke) „einfängt“.

Beispiele

Beispiele zu den Vermessungsaufgaben von Jutta Gut (mit Lösungen)

$\rightarrow$ nächste Seite ...

Inhaltsverzeichnis

1 Vertiefung: Betrachtungen im Einheitskreis
- 1.1 Gradmaß und Bogenmaß im Einheitskreis
- 1.2 Sinus, Cosinus und Tangens im Einheitskreis
  - 1.2.1 Theorie
  - 1.2.2 Wichtige Werte

Vertiefung: Betrachtungen im Einheitskreis

Gradmaß und Bogenmaß im Einheitskreis

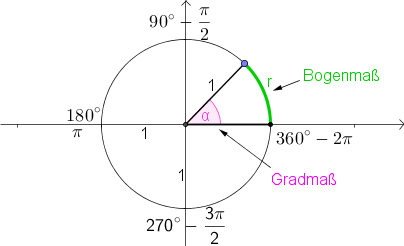
Einheitskreis mit Winkel in Grad- und Bogenmaß

Der Einheitskreis ist ein Kreis mit Radius $r=1$. Sein Umfang beträgt $$U=2\cdot r\cdot \pi=2\cdot 1\cdot \pi=2\pi$$

Legt man durch den Mittelpunkt des Einheitskreises das Koordinatensystem, so kann man den Winkel zwischen der positiven $x$-Achse und einem beliebig eingezeichneten Radius auf zwei Arten bestimmen:

1) Gradmaß (abgekürzt mit °)

So haben wir bis jetzt immer Winkel gemessen.

Eine volle Umdrehung hat $360°$.
Eine halbe Umdrehung hat $180°$.

2) Bogenmaß (abgekürzt $rad$ für engl. radian)

Anstelle der Grad kann auch die Länge des Kreisbogens $r$ (siehe Skizze) bestimmt werden.

Bei einer vollen Umdrehung hat $r$ die Länge $2\cdot \pi$ ($=$ Umfang des Einheitskreises, siehe oben). Somit beträgt der Winkel $2\pi\ rad$.
Eine halbe Umdrehung entspricht dem Winkel $\pi$ $rad$.

$Aha!$ : Das folgende Arbeitsblatt hilft dir, den Zusammenhang von Bogenmaß und Gradmaß zu verstehen

Sollte das Applet nicht funktionieren, klicke hier.

Merke

Die Umrechnung von Grad- in Bogenmaß (und umgekehrt) funktioniert am einfachsten mit einer Schlussrechnung:

$$ 360°\ \ \ - \ \ \ 2\pi \textrm{ rad}$$

$$ \alpha°\ \ \ - \ \ \ \alpha \textrm{ rad}$$ Wobei entweder $\alpha°$ (der Winkel in Gradmaß) oder $\alpha$ rad (der Winkel in Bogenmaß) gegeben ist.

Musterbeispiel

a) Wandeln Sie den Winkel $\alpha=90°$ in Bogenmaß um.

b) Wandeln Sie den Winkel $\alpha=\frac{\pi}{3}$ rad in Gradmaß um.

Lösung

a) Grad- in Bogenmaß: $$ 360°\ \ \ - \ \ \ 2\pi \textrm{ rad}$$ $$ \textbf{90°}\ \ \ - \ \ \ \alpha \textrm{ rad}$$ $$\rightarrow \ \alpha \textrm{ rad}=\frac{90\cdot 2\pi}{360}=\frac{\pi}{2} \textrm{ rad}$$

A: $90°$ entsprechen in Bogenmaß $\frac{\pi}{2} \textrm{ rad}$.

b) Bogen- in Gradmaß: $$ 360°\ \ \ - \ \ \ 2\pi \textrm{ rad}$$ $$ \alpha°\ \ \ - \ \ \ \mathbf{\frac{\pi}{3} \textrm{ rad}}$$ $$\rightarrow \ \alpha°=\frac{360\cdot \frac{\pi}{3}}{2\pi}=60°$$

A: $\frac{\pi}{3}$ rad entsprechen $60°$.

Sinus, Cosinus und Tangens im Einheitskreis

Theorie

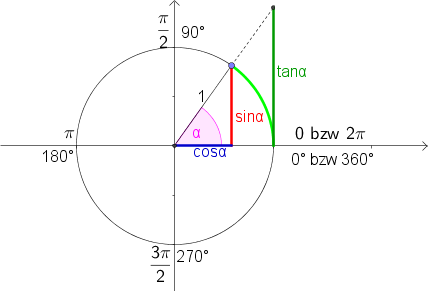
Sinus, Cosinus und Tangens können folgendermaßen aus dem Einheitskreis abgelesen werden:

Sinus, Cosinus und Tangens im Einheitskreis

Der Sinus entspricht der Länge der rot markierten Stecke $= y$-Koordinate des Punktes auf dem Einheitskreis.

Der Cosinus entspricht der Länge der blau markierten Stecke $= x$-Koordinate des Punktes auf dem Einheitskreis.

Der Tangens entspricht der Länge des Tangentenabschnittes der Tangente durch den Punkt $(1,0)$.

Begründung:

für den Sinus: Betrachte das rechtwinklige Dreieck im Einheitskreis. Die Hypotenuse ist der Radius und hat somit die Länge $1$. Die Länge der $\color{red}{\textrm{roten Strecke}}$ ist von $\alpha$ aus gesehen die Gegenkathete GK.

Zu zeigen ist nun: $$\sin \ \alpha=\color{red}{\textrm{rote Strecke}}$$

Beweis: $$\sin\ \alpha=\frac{GK}{H}=\frac{\color{red}{\textrm{rote Strecke}}}{1}=\color{red}{\textrm{rote Strecke}}$$ Somit gilt: $$\sin\ \alpha=\color{red}{\textrm{rote Strecke}}$$

Der Beweis für den Cosinus funktioniert analog. Für den Tangens muss das große Dreieck mit AK $=1$ betrachtet werden.

$Aha!$ : Das folgende Arbeitsblatt zeigt dir den Zusammenhang von Sinus, Cosinus und Tangens im Einheitskreis:

Sollte das Applet nicht funktionieren, klicke hier.

Wichtige Werte

Die folgende Tabelle gibt Werte für Sinus, Cosinus und Tangens an, die du nun auch ohne technische Unterstützung, allein durch die Vorstellung vom Einheitskreis, wissen solltest. Das obige Arbeitsblatt sollte dir dabei helfen:

	Sinus	Cosinus	Tangens
Gradmaß: $90°$ Bogenmaß:$\frac{\pi}{2}$ rad	$1$	$0$	nicht definiert
$180°$ $\pi$ rad	$0$	$-1$	$0$
$270°$ $\frac{3\pi}{2}$ rad	$-1$	$0$	nicht definiert
$0°$ und $360°$ 0 rad und $2\pi$ rad	$0$	$1$	$0$

$\rightarrow$ nächste Seite ...

Inhaltsverzeichnis

1 Trigonometrische Funktionen
2 Bedeutung der Parameter - Manipulation der Sinusfunktion

Trigonometrische Funktionen

Trägt man ausgehend vom Einheitskreis die Werte des Sinus in Abhängigkeit der Bogenlänge ab, so erhält man die Sinusfunktion. Analog funktioniert dies für die Cosinus- und Tangensfunktion, wie das folgende Applet zeigt:

Was ist zu tun?

Verschiebe im linken Grafikfenster den Punkt auf dem Kreis (oder klicke links unten auf den „Play“-Button. Im rechten Grafikfenster wird der Sinus in Abhängigkeit vom Winkel (in Bogenmaß) abgetragen und es entsteht die typische Sinusfunktion. Versuche dies anschließend auch mit der Cosinus- und Tangensfunktion, indem du im rechten Grafikfenster das entsprechende Kästchen anklickst.

Falls dieses Applet nicht funktioniert, klicke hier

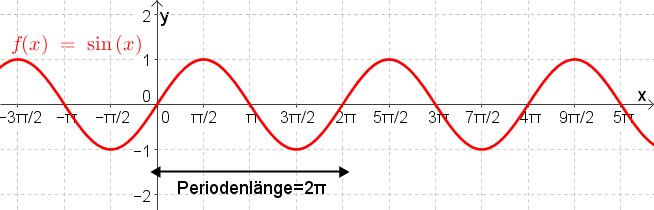
Sinusfunktion $f(x)=\sin(x)$

Stellt man den Sinus in Abhängigkeit vom Winkel graphisch dar, indem man auf der $x$-Achse den Winkel in Bogenmaß und auf der $y$-Achse den zugehörigen Sinuswert angibt, so entsteht der folgende Graph:

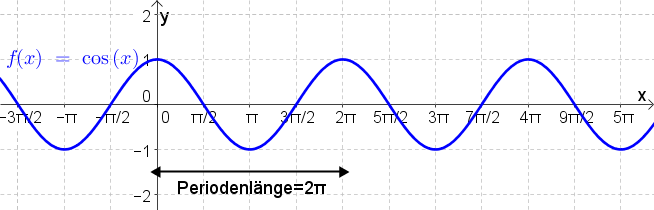
Graph der Sinusfunktion mit Kennzeichnung der Periodenlänge von $2\pi$

Cosinusfunktion $f(x)=\cos(x)$

Der Graph der Cosinusfunktion hat die folgende Form:

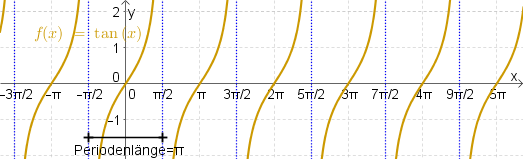
Graph der Cosinusfunktion mit Kennzeichnung der Periodenlänge von $2\pi$

Tangensfunktion $f(x)=\tan(x)$

Der Graph der Tangensfunktion hat die folgende Form:

Graph der Tangensfunktion samt den Asymptoten (rot) und der Kennzeichnung der Periodenlänge von $\pi$

Besondere Eigenschaften der trigonometrischen Funktionen

Periodizität: Die Werte der trigonometrischen Funktionen wiederholen sich in regelmäßigen Abständen.
Beschränktheit: Sinus- und Cosinusfunktion haben die Wertemenge $\mathbb{W}=[-1;1]$. Anders formuliert: es gilt für alle $x$: $$|\sin(x)|\leq 1$$ und $$|\cos(x)|\leq 1 $$ (Hinweis: Hier wurde der Betrag verwendet.)
Der Tangens ist unbeschränkt (geht nach $-\infty$ und $+\infty$) und hat unendlich viele vertikale Asymptoten im Abstand von $\frac{\pi}{2}$.
Wichtige Funktionswerte (Nullstellen, Hoch- und Tiefpunkte) können bereits aus der Tabelle zum Einheitskreis herausgelesen werden.

Bedeutung der Parameter - Manipulation der Sinusfunktion

Dieses GeoGebra-Applet zeigt dir die wichtigsten Parameter, um den Graphen einer Sinusfunktion oder einer Cosinusfunktion zu verändern.

$\rightarrow$ nächste Seite ...

Inhaltsverzeichnis

1 Das allgemeine Dreieck - Sinussatz und Cosinussatz

Das allgemeine Dreieck - Sinussatz und Cosinussatz

Wichtig: Der folgende Abschnitt ist für die schriftliche Matura nur in folgenden Schulzweigen relevant:

Allerdings helfen dir die hier beschriebenen Formeln, gewisse Beispiele schneller und einfacher zu berechnen. Daneben könnte dieser Abschnitt auch bei der mündlichen Matura zum Stoffgebiet gehören (Informationen dazu gibt dir deine Lehrperson).

allgemeines Dreieck

Unter allgemeinen Dreiecken versteht man Dreiecke, die nicht über einen rechten Winkel verfügen müssen.

Ohne rechten Winkel können wir die Formeln für Sinus, Cosinus und Tangens nicht verwenden. Aus diesem Grund führen wir nun neue Formeln ein:

a) den Sinussatz

b) den Cosinussatz und

c) die allgemeinen Flächenformeln

Im allgemeinen Dreieck braucht man immer $3$ bekannte Größen, um eine vierte zu berechnen! (Im rechtwinkligen Dreieck reichten uns dank dem rechten Winkel zwei zusätzlich Größen, um eine weitere zu berechnen).

Sinussatz

Der Sinussatz wird verwendet, wenn im allgemeinen Dreieck

1. eine Seite und

2. der gegenüberliegende Winkel und

3. irgendeine andere Seite oder ein anderer Winkel bekannt sind.

Formel für den Sinussatz

$$\frac{\sin\ \alpha}{a}=\frac{\sin\ \beta}{b}=\frac{\sin\ \gamma}{c}$$

Das Video auf der rechten Seite zeigt dir auf musikalische Art und Weise die Herleitung des Sinussatzes:

Cosinussatz

Das Video auf der rechten Seite zeigt dir auf musikalische Art und Weise die Herleitung und die Bedeutung des Cosinussatzes:

Formeln für den Cosinussatz
$ a^2=b^2+c^2-2\cdot b\cdot c\cdot \cos\ \alpha$ $b^2=a^2+c^2-2\cdot a\cdot c\cdot \cos\ \beta$ $c^2=a^2+b^2-2\cdot a\cdot b\cdot \cos\ \gamma$

Der Cosinussatz wird verwendet, wenn im allgemeinen Dreieck:

1. $2$ Seiten und der darin eingeschlossene Winkel gegeben ist oder

2. alle drei Seiten gegeben sind und ein Winkel berechnet werden will.

Voraussetzungen, um den Cosinussatz zu verwenden.

gegebene Größen

berechenbare Größen

Zwei Seiten und der eingeschlossene Winkel sind gegeben, die gegenüberliegende Seite kann berechnet werden

Drei Seiten sind gegeben, ein Winkel kann berechnet werden

Beispiele

Aufgaben zum allgemeinen Dreieck von Jutta Gut (mit Lösungen)

$\rightarrow$ nächste Seite ...

Zusammenfassung der wichtigsten Formeln im rechtwinkligen und im allgemeinen Dreieck

	Rechtwinkliges Dreieck	Allgemeines Dreieck
Winkelsumme	$180°=\alpha+\beta+\gamma$	$180°=\alpha+\beta+\gamma$
Pythagoras	$HYP^2=GK^2+AK^2$	gilt nur im rechtwinkligen Dreieck!
Flächeninhalt	$A=\frac{GK\cdot AK}{2}$	$A=\frac{a\cdot h_a}{2}=\frac{b\cdot h_b}{2}=\frac{c\cdot h_c}{2}$
Sinus	$\sin \alpha =\frac{GK}{HYP}$	Diese Formel gilt nur im rechtwinkligen Dreieck!
Cosinus	$\cos\alpha =\frac{AK}{HYP}$	Diese Formel gilt nur im rechtwinkligen Dreieck!
Tangens	$\tan\alpha =\frac{GK}{AK}$	Diese Formel gilt nur im rechtwinkligen Dreieck!
Sinussatz		$\frac{\sin\alpha}{a}=\frac{\sin\beta}{b}=\frac{\sin\gamma}{c}$
Cosinussatz		$a^2=b^2+c^2-2\cdot b\cdot c\cdot \cos\alpha$ $b^2=a^2+c^2-2\cdot a\cdot c\cdot \cos\beta$ $c^2=a^2+b^2-2\cdot a\cdot b\cdot \cos\gamma$