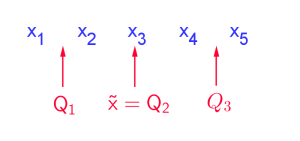Beschreibende Statistik
- Einleitung
- Daten und Diagramme
- Schummeln mit Statistik
- Interaktive Übungen
- Zentralmaße - statistische Kennzahlen für das Mittel
- Streuungsmaße - statistische Kennzahlen für die Streuung
- Maturaaufgaben
- Berechnung der Kennzahlen mit Technologie
- Regression
In der beschreibenden Statistik beschäftigen wir uns mit der Auswertung von Datenmengen. Die Auswertung erfolgt dabei über graphische Darstellungsformen (Diagramme) und einzelne aussagekräftige Kennzahlen (z. B. Mittelwert, Spannweite, ...), mit denen Rückschlüsse auf die Grundgesamtheit aller Daten gezogen werden können.
$Step\ by\ Step!$ $\ $ Weiterer Lernpfad zur beschreibenden Statistik
Begriffe
$n...$ Umfang der Stichprobe
$x_1...$ Zahl an der 1. Stelle
$x_i...$ Zahl an der $i.$ Stelle
$\{ x_1;x_2;.....;x_n \} ...$ Stichprobe (z. B. $\{ 1; 2; 5; 5; 5; 10;\}$ )
$a_1...$ erster Wert, der in der Stichprobe vorkommt (im oberen Beispiel ist $a_1=1$)
$a_4...$ vierter Wert, der in der Stichprobe vorkommt (im oberen Beispiel ist $a_4=10$)
$a_i...$ $i.$ Wert, der in der Stichprobe vorkommt
Arten von Merkmalen/Daten
Im Groben unterscheidet man zwischen $3$ Arten von Merkmalen:
- Nominale Merkmale können nicht sinnvoll durch eine Zahl beschrieben oder in eine Reihenfolge gebracht werden. Beispiele sind „Geschlecht“ und „Haarfarbe“.
- Ordinale Merkmale können in eine Reihenfolge gebracht werden, eignen sich aber nicht für Rechnungen (wie z. B. Addition). Beispiele sind „Platzierung bei einem Rennen“ und „Bildungsabschlüsse“.
- Metrische Merkmale können durch Zahlen beschrieben werden, mit denen man auch rechnen kann. Beispiele sind „Gehalt“, „Alter“ und „Schuhgröße“.
Absolute und relative Häufigkeit
|
Die absolute Häufigkeit $H_i$ gibt an, wie oft das $i-$te Element in der Stichprobe auftritt.
Z. B.: In der Menge $\{ 1;2;2;2;4;4;6\}$ ist die absolute Häufigkeit der Zahl $2$ genau $H=3$, da die $2$ insgesamt dreimal vorkommt. |
In einer (kleinen) Umfrage werden von $n=15$ Personen die Schuhgrößen gemessen. Das Ergebnis ist in der folgenden Liste angegeben:
$$\{36;36;36;37;37;37;37;38;38;40;41;42;42;42;46\}$$
Aufgabe: Ermitteln Sie in einer Tabelle die Häufigkeit jedes Merkmals ($=a_i$).
{
| Werte $a_i$ $\\ $ | Häufigkeiten $H_i$ $\\ $ |
|---|---|
| 36 | 3 |
| 37 | 4 |
| 38 | 2 |
| 40 | 1 |
| 41 | 1 |
| 42 | 3 |
| 46 | 1 |
| Summe | 15 |
Aus der absoluten Häufigkeit kann man noch nicht darauf schließen, ob ein Merkmal wirklich häufig auftritt oder nicht, da es immer auch auf die Gesamtanzahl $n$ der untersuchten Werte ankommt.
So ist eine absolute Häufigkeit von $100$ für $n=150$ sehr groß, für $n=1$ Mrd. dagegen wohl eher klein.
In solchen Fällen ist es hilfreich zu wissen, wie viel Prozent der Gesamtmenge $n$ dieses Merkmal besitzen. Dies wird berechnet mit ...
|
Die relative Häufigkeit $h_i$ gibt an, mit wie viel Prozent ein Merkmal in Bezug auf die Gesamtmenge $n$ auftritt. Es gilt:
$$h_i=\frac{H_i}{n}$$ Z. B.: In der Menge $\{1;2;2;2;4;4;6\}$ ist die absolute Häufigkeit der Zahl $2$ genau $H=3$, die relative Häufigkeit ergibt sich dann mit: $$h=\frac{H}{n}=\frac{3}{7}\approx 43\%$$ |
Berechnen Sie mithilfe der Tabelle aus der Schuhgrößenumfrage (siehe oben) die relativen Häufigkeiten $h_i$.
| Werte $a_i$ | absolute Häufigkeiten $H_i$ | relative Häufigkeiten $h_i$ |
|---|---|---|
| 36 | 3 | $\ \ \ $ |
| 37 | 4 | |
| 38 | 2 | |
| 40 | 1 | |
| 41 | 1 | |
| 42 | 3 | |
| 46 | 1 | |
| Summe | 15 |
$n=15$ {
| Werte $a_i$ | absolute Häufigkeiten $H_i$ | relative Häufigkeiten $h_i$ |
|---|---|---|
| 36 | 3 | $\frac{3}{15}=20$% |
| 37 | 4 | $\frac{4}{15}=26.7$% |
| 38 | 2 | $\frac{2}{15}=13.3$% |
| 40 | 1 | $\frac{1}{15}=6.7$% |
| 41 | 1 | $\frac{1}{15}=6.7$% |
| 42 | 3 | $\frac{3}{15}=20$% |
| 46 | 1 | $\frac{1}{15}=6.7$% |
| Summe | 15 | $\frac{15}{15}=100$% |
Diagramme
Säulen- und Balkendiagramm
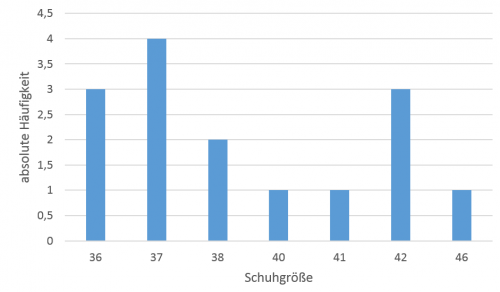
In Säulendiagrammen gibt die $y$-Achse die absolute Häufigkeit (oder relative Häufigkeit) eines Merkmals auf der $x$-Achse an.
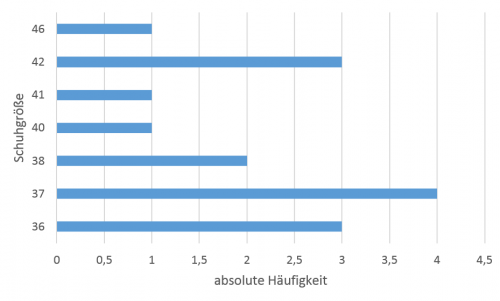
Bei Balkendiagrammen sind die Achsen vertauscht.
Histogramm
Analog zum Säulen- und Balkendiagramm können absolute Zahlen und Prozentsätze auch in einem Histogramm dargestellt werden. In beiden Fällen ist auf eine geeignete Beschriftung der Achsen zu achten. Im Unterschied zu einem Säulendiagramm entsprechen die absoluten oder relativen Häufigkeiten nun nicht mehr den Höhen der Säulen, sondern den rechteckigen Flächen der Säulen. Auf Zwischenräume bei den einzelnen Säulen kann auch verzichtet werden. Bei einem Histogramm mit Klasseneinteilung werden zuerst die Werte zu Klassen zusammengefasst, wobei möglichst gleich breite Klassen anzustreben sind. Für die Höhe der Rechtecke gilt:
$$\text{Rechteckshöhe}=\frac{\text{absolute bzw. relative Häufigkeit}}{\text{Klassenbreite}}$$
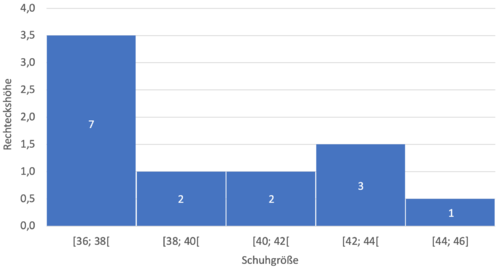
Im Beispiel fassen wir die Schuhgrößen in Klassen mit der Klassenbreite $2$ zusammen und erstellen eine Häufigkeitstabelle.
| Schuhgrößen | absolute Häufigkeiten $H_i$ | relative Häufigkeiten $h_i$ | Rechteckshöhe |
|---|---|---|---|
| $[36; 38[$ | $7$ | $\frac{7}{15}=46.7 \% $ | $\frac{7}{2}=3.5$ bzw. $\frac{46.7}{2}=23.3$ |
| $[38; 40[$ | $2$ | $\frac{2}{15}=13.3 \%$ | $\frac{2}{2}=1$ bzw. $\frac{13.3}{2}=6.7$ |
| $[40; 42[$ | $2$ | $\frac{2}{15}=13.3 \%$ | $\frac{2}{2}=1$ bzw. $\frac{13.3}{2}=6.7$ |
| $[42; 44[$ | $3$ | $\frac{3}{15}=20 \%$ | $\frac{3}{2}=1.5$ bzw. $\frac{20}{2}=10$ |
| $[44; 46]$ | $1$ | $\frac{1}{15}=6.7 \%$ | $\frac{1}{2}=0.5$ bzw. $\frac{6.7}{2}=3.3$ |
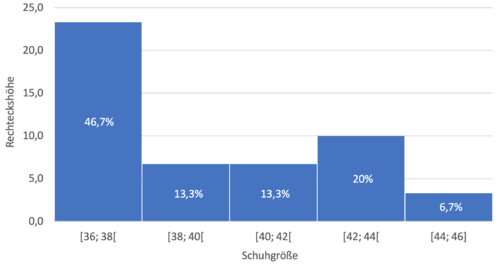
Anhand der Daten aus der Tabelle lassen sich abschließend Histogramme mit absoluten bzw. relativen Häufigkeiten erstellen.
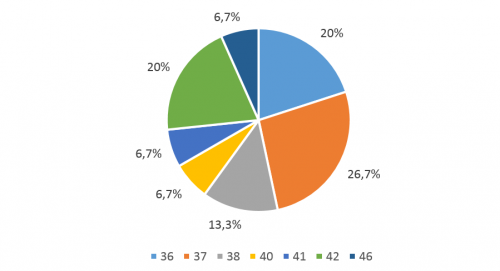
Kreisdiagramm
Bei Kreisdiagrammen entspricht ein Kreissegment der relativen Häufigkeit eines Merkmals. Alle Kreissegmente zusammen (d. h. alle relativen Häufigkeiten) ergeben einen ganzen Kreis (d. h. $100 \%$).
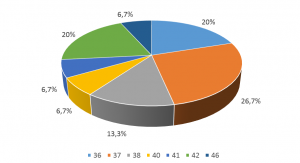
|
Schummeln mit Kreisdiagrammen Bei dreidimensionalen Kreisdiagrammen erscheinen Segmente im hinteren Bereich kleiner als Segmente im vorderen Bereich. Deshalb sollte man auf den 3d-Effekt verzichten. |
Boxplot (Kastenschaubild)
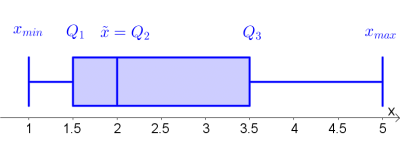
Boxplot-Diagramme geben einen Überblick über die Verteilung der Daten, indem Sie die Datenreihe in vier $25 \%$-Bereiche teilen. Hierbei bildet der Bereich zwischen den Quartilen den „Kasten“, von dem aus die Antennen zum minimalen und maximalen Wert gehen ($x_{min}$ und $x_{max}$).
|
In jedem der $4$ Bereiche eines Boxplot-Diagramms liegen ca. $25 \%$ aller Werte |
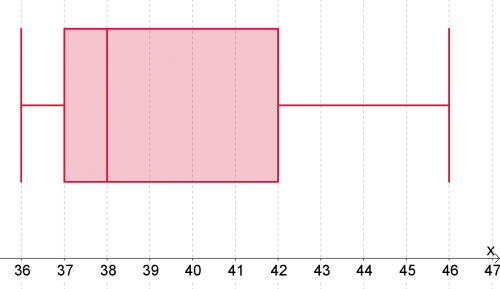
Gegeben ist das folgende Boxplot-Diagramm, das aus den Daten der Schuhgrößen erstellt wurde.
Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind und begründen Sie diese Entscheidung:
- Die Anzahl der Werte zwischen $36$ und $37$ ist mit Sicherheit geringer als die Anzahl der Werte zwischen $42$ und $46$.
- Weniger als $25 \%$ aller Werte sind kleiner oder gleich $42$.
- Falsch! Da jeder Bereich ca. $ 25 \%$ aller Werte umfasst, liegen in beiden Bereichen ungefähr gleich viele Werte.
- Falsch! Es sind mindestens $75 \%$ aller Werte kleiner oder gleich $42$ (oder weniger als $25 \%$ aller Werte sind größer als $42$).
Hilfreiche GeoGebra-Applets
- Boxplot (Andreas Lindner): https://www.geogebra.org/m/n59E5Dtm
- Boxplot Game (Barbara Baker): https://www.geogebra.org/m/JRgG3xec
- Median und arithmetischer Mittelwert (Sandi Reichenberger): https://www.geogebra.org/m/hK3SSww7
- Sammlung von Statistik-Applets (Kurt Söser): https://www.geogebra.org/m/R2ABEB3M
Manipulieren von Liniendiagrammen
Die folgende Tabelle bildet die Grundlage für das Einführungsbeispiel:
Anzahl der im Straßenverkehr Getöteten in Österreich:
|
Jahr |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
|
Getötete |
1210 |
1027 |
1105 |
963 |
1079 |
976 |
958 |
956 |
931 |
878 |
768 |
730 |
691 |
679 |
633 |
552 |
521 |
531 |
455 |
430 |
475 |
Quelle: Statistik Austria
Das entsprechende Liniendiagramm sieht folgendermaßen aus:
Die an sich schon beeindruckende Statistik kann aber durchaus noch beeindruckender dargestellt werden, indem verschiedene Manipulationsmöglichkeiten angewendet werden.
Gezielte Auswahl der Datenreihe
In den Jahren 1999 bis 2014 sind die Werte bis auf eine kleine Ausnahme immer gesunken. Diese Daten nehmen wir im folgenden Diagramm.
Verkürzung der $y$-Achse
Um das Sinken der Werte noch deutlicher zu machen, wird die $y$-Achse erst bei $400$ gestartet.
Schon beeindruckender, nicht?
Dehnen und Stauchen der Achsen
Eine einfache Art, die Steilheit des Graphen zu verändern, ist das Stauchen der $x$-Achse bzw. entsprechendes Dehnen der $y$-Achse.
Quiz: Beschreibende Statistik (WS 1.1-1.4)
Um „das Mittel“ zu berechnen, gibt es verschiedene Möglichkeiten. Dabei hat jede Vor- und Nachteile:
Arithmetisches Mittel $\bar{x}$
Definition
Das arithmetische Mittel, auch Durchschnitt oder Mittelwert genannt, ist nur bei metrisch skalierten Merkmalen anwendbar und wird berechnet, indem man alle vorhandenen Werte addiert und die Summe dieser Werte dann durch die Gesamtanzahl der Werte dividiert.
Beachte: Es gibt Merkmale in Datenlisten, die eine Berechnung des arithmetischen Mittels unmöglich machen (z. B.: Augenfarben, Güteklassen, …). Auch bei Schulnoten, genauer zur Berechnung einer „Durchschnittsnote“, wird oftmals das arithmetische Mittel fälschlicherweise herangezogen. Schulnoten sind ausschließlich ordinal skaliert, denn die Abstände zwischen den Noten sind nicht genauer definiert.
Beispiel: Bei einem Test erzielten $5$ Teilnehmer*innen folgende Punktezahlen: $\{ 1;2;2;2;5\}$. Das arithmetische Mittel (= „Durchschnittspunktezahl“) ergibt:
$$\bar{x}=\frac{1+2+2+2+5}{5}=\frac{12}{5}=2.4$$
|
Das arithmetische Mittel $\bar{x}$ ist definiert als
$$\bar{x}=\frac{x_1+x_2+...+x_n}{n}$$ $$(\text{Summe aller Werte dividiert durch die Gesamtanzahl})$$ Formal mithilfe des Summenzeichens: $$\bar{x}=\frac{1}{n}\cdot \sum_{i=1}^{n} x_i$$ |
Idee des arithmetischen Mittels als Schwerpunkt
| Übung zur Definition einer Menge |
|---|
|
|
| Falls das Applet nicht angezeigt wird, klicke hier. |
Das gewichtete arithmetische Mittel
Sind bereits die absoluten oder relativen Häufigkeiten für das arithmetische Mittel bekannt, so kann auch eine der folgenden Formeln für das „gewichtete arithmetische Mittel“ verwendet werden:
|
Formel mit der absoluten Häufigkeit
$$\bar{x}=\frac{a_1\cdot H_1+a_2\cdot H_2+...}{n}=\frac{1}{n}\cdot \sum_{i} a_i\cdot H_i$$ $$(\text{Summe aller Werte mal deren absolute Häufigkeit dividiert durch die Gesamtanzahl})$$ |
Beispiel zur Berechnung des arithmetischen Mittels mithilfe der absoluten Häufigkeiten:
Gegeben sind die folgenden Punktezahlen: $\{ 1;2;2;2;5\} $. Zuerst erstellen wir die Häufigkeitstabelle:
| Punktezahl $a_i$ | $H_i$ | $h_i$ |
|---|---|---|
| 1 | 1 | $\frac{1}{5}=20 \%$ |
| 2 | 3 | $\frac{3}{5}=60 \%$ |
| 5 | 1 | $\frac{1}{5}=20 \%$ |
| $\sum$ | 5 | $\frac{5}{5}=100 \%$ |
Setzen wir in die Formel für die absolute Häufigkeit ein, so erhalten wir
$$\bar{x}=\frac{a_1\cdot H_1+a_2\cdot H_2+a_3\cdot H_3}{n}$$
$$\bar{x}=\frac{1\cdot 1+2\cdot 3+5\cdot 1}{5}=\frac{12}{5}=2.4$$
|
Formel mit der relativen Häufigkeit
$$\bar{x}=a_1\cdot h_1+a_2\cdot h_2+...=\sum_{i} a_i\cdot h_i $$ $$(\text{Summe aller Werte mal deren relative Häufigkeit})$$
|
Beispiel zur Berechnung des arithmetischen Mittels mithilfe der relativen Häufigkeiten:
Gegeben sind die Punktezahlen $\{ 1;2;2;2;5\} $. Um das arithmetische Mittel zu berechnen, lesen wir die Werte sowie die relativen Häufigkeiten aus der Häufigkeitstabelle und setzen in die Formel ein:
| Punktezahl $a_i$ | $H_i$ | $h_i$ |
|---|---|---|
| 1 | 1 | $\frac{1}{5}=20 \%$ |
| 2 | 3 | $\frac{3}{5}=60 \%$ |
| 5 | 1 | $\frac{1}{5}=20 \%$ |
| $\sum$ | 5 | $\frac{5}{5}=100 \%$ |
$$\bar{x}=a_1\cdot h_1+a_2\cdot h_2+a_3\cdot h_3=1\cdot \frac{1}{5}+2\cdot \frac{3}{5}+5\cdot \frac{1}{5}$$
$$\bar{x}=\frac{12}{5}=2.4$$
Zusammenfassung
|
|
Neben dem arithmetischen Mittel gibt es nun noch einen weiteren wichtigen Zentralwert, den ...
Median $Q_2$ ($=$ mittleres oder 2. Quartil)
|
Sortiert man eine Datenliste der Größe nach, so ist der Median $Q_2$ der Wert in der Mitte der geordneten Liste.
Liegen genau zwei Werte in der Mitte (was immer dann der Fall ist, wenn die Anzahl der Werte $n$ gerade ist), so ist $Q_2$ das arithmetische Mittel dieser beiden Werte.
Formal: $\begin{align} &Q_2=x_{\frac{n+1}{2} }&& \textrm{ für ungerade $n$}\\ &Q_2=\frac{1}{2}\cdot \left(x_{\frac{n}{2} }+ x_{\frac{n}{2}+1 } \right)&& \textrm{ für gerade $n$}\\ \end{align}$ |
Beispiel für den Median
Gegeben ist die folgende Liste an Punktezahlen: $\{1;2;2;2;5\}$. Ermitteln Sie den Median $Q_2$.
Lösung: Insgesamt sind es $n=5$ Werte. Da die Liste bereits nach Größe geordnet ist, können wir den Median einfach ablesen:
| durch Ablesen | $\{1;2;\color{red}{2};2;5\}$ |
| rechnerisch | $Q_2=x_{\frac{5+1}{2}}=x_3=2$ |
Antwort: Der Median $Q_2$ ist der Wert an der dritten Stelle und somit $Q_2=2$.
$Aha!$ $\ $ Mithilfe dieses Applets kannst du die wichtigsten Eigenschaften des arithmetischen Mittels (Mittelwert) und des Medians noch einmal überprüfen.
Vorteil des Medians - Nachteil des arithmetischen Mittels
Vergleichen wir noch einmal das arithmetische Mittel und den Median unserer Liste $\{1; 2; 2; 2; 5\}$. $$\bar{x}=2.4 \textrm{ und } Q_2=2$$ Warum ist das arithmetische Mittel größer als der Median?
Antwort: Der Grund liegt darin, dass das arithmetische Mittel durch den „Ausreißer“ $5$ verzerrt wurde. Der Median hat sich dadurch nicht verändert.
|
Allgemein gilt:
Hinweis: Als Ausreißer gelten Zahlen, die im Vergleich zu den anderen Werten sehr klein oder sehr groß sind. |
$Aha!$ $\ $ Zur besseren Verdeutlichung kannst du dir dieses Arbeitsblatt ansehen (klicke dabei zuerst auf „Median“ und „Mittelwert“ und verändere dann die Zahlen).
Aufgaben zum Arbeitsblatt
- Setze „Zahl der Datenwerte“ auf $5$.
- Schiebe nun $4$ Werte auf „$1$“ und einen auf „$4$“. Wie verhält sich der Median, wie der Mittelwert?
- Verteile anschließend alle $5$ Werte gleichmäßig auf den Zahlengeraden.
- Nimm dann den ganz linken Wert und verschiebe ihn langsam ganz nach rechts. Beobachte dabei, wann und wie sich Median und arithmetisches Mittel verändern.
Lösungen:
1. Der Median ist der mittlere Wert aller $5$ Werte und bleibt deshalb bei $1$. Der Mittelwert liegt dagegen zwischen $1$ und $4$.
2. Der Median bleibt gleich, solange der zu verschiebende Wert nicht in der Mitte ist. Der Mittelwert ändert seinen Wert ständig.
Hinweis: Ein etwas komplexeres Arbeitsblatt findest du hier.
Modus/Modalwert
|
Der Modus (auch Modalwert genannt) ist der häufigste Wert in einer Datenreihe (d. h. jener Wert mit der größten absoluten Häufigkeit).
Dann ist der Modus gleich $2$, da $2$ mit einer absoluten Häufigkeit von $H=3$ erscheint. |
Geometrisches Mittel
Das Geometrische Mittel wird verwendet, um einen „durchschnittlichen Faktor“ zu ermitteln. So kann damit beispielsweise der durchschnittliche Wachstumsfaktor oder die durchschnittliche Verzinsung berechnet werden.
|
Sind $r_1,\ ...,\ r_5$ verschiedene Wachstumsfaktoren, dann ist
$$\bar{x}_{geo}=\sqrt[n]{r_1\cdot r_2\cdot r_3\dots r_n}$$ der durchschnittliche Wachstumsfaktor.
|
Das jährliche Wachstum eines Kapitals von $K_0=100$ Euro ist in folgender Tabelle gegeben.
| Jahr | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Verzinsung | 5 % | 3 % | -4 % | 2 % | -1 % |
a) Berechnen Sie das Kapital am Ende des $5$. Jahres.
b) Ermitteln Sie um welchen Prozentsatz das Kapital durchschnittlich pro Jahr gewachsen ist.
Wiederholung: Aufzinsen heißt, mit dem Wachstumsfaktor $r$ multiplizieren. $$K_5=K_0\cdot r_1\cdot r_2\cdot r_3\cdot r_4\cdot r_5$$ $$K_5=100\cdot 1.05\cdot 1.03\cdot 0.96\cdot 1.02\cdot 0.99$$ $$K_5=104.84$$
Antwort: Das Kapital nach $5$ Jahren beträgt $€ 104.84$.
b) Ermitteln Sie um welchen Prozentsatz das Kapital durchschnittlich pro Jahr gewachsen ist.
Hier gibt es nun $2$ Möglichkeiten:
1. Möglichkeit: mithilfe des geometrischen Mittels
$$\bar{x}_{geo}=\sqrt[n]{r_1\cdot r_2\cdot r_3 \dots r_n}$$
$$\bar{x}_{geo}=\sqrt[5]{1.05\cdot 1.03\cdot 0.96\cdot 1.02\cdot 0.99}$$
$$\bar{x}_{geo} = 1.0095$$
Der durchschnittliche Zinssatz beträgt $0.95 \%$.
2. Möglichkeit: mithilfe des Anfangs- und Endkapitals und der Formel $K_n=K_0\cdot r^n$
Wir wissen: $K_0=100$ und $K_5=104.84$.
Gesucht ist nun der durchschnittliche Aufzinsungsfaktor $r$ in der Zinseszinsformel $K_n=K_0\cdot r^n$:
$$K_n=K_0\cdot r^n$$ $$104.84=100\cdot r^5$$ $$r=1.0095$$ Der durchschnittliche Zinssatz beträgt $0.95 \%$.
Streuung von Daten
Im vorigen Kapitel haben wir gelernt, wie wir verschiedene Arten von Zentralmaßen bestimmen. Ein Zentralmaß allein sagt uns allerdings noch nicht viel über die Verteilung (= Streuung) der Werte aus.
Beide Datenmengen in den Abbildungen haben denselben Mittelwert, aber unterschiedliche Streuungen. Die Werte im rechten Bild liegen näher um den Mittelwert $1$ als die Werte im linken Bild.
Aus diesem Grund lernen wir nun noch zusätzliche Kennzahlen für die Streuung von Werten kennen, um solche Datenmengen besser unterscheiden zu können.
Spannweite
|
Die Spannweite ist die Differenz (Abstand) zwischen dem kleinsten und dem größten Wert der Datenmenge.
$$\text{Spannweite}=x_{max}-x_{min}$$ |
Beispiel: Gegeben sei die Datenliste $\{1;2;2;2;5\}$. Bestimme die Spannweite.
Lösung: $x_{max}=5;\ x_{min}=1$ $$\text{Spannweite}=x_{max}-x_{min}=5-1=4$$
Antwort: Die Spannweite beträgt $4$.
Varianz und Standardabweichung
Eine andere Möglichkeit, um die Streuung anzugeben wäre folgende: Wir berechnen den durchschnittlichen Abstand aller Werte vom arithmetischen Mittel $\bar{x}$. Diesen durchschnittlichen Abstand nennen wir Standardabweichung oder kurz $\sigma$ (= sigma).
Herleitung der Standardabweichung:
Um die durchschnittlichen Abstände aller Werte vom arithmetischen Mittel $\bar{x}$ (= Standardabweichung) zu erhalten, machen wir Folgendes:
- Schritt: Wir berechnen den Abstand aller Werte von $\bar{x}$:
- $$(x_1-\bar{x}) \textrm{ und } (x_2-\bar{x}) \textrm{ und ... und } (x_n-\bar{x})$$
- Schritt: Da die Abstände mitunter negativ sind (wenn $x_i<\bar{x}$), quadrieren wir alle Abstände:
- $$(x_1-\bar{x})^2 \textrm{ und } (x_2-\bar{x})^2 \textrm{ und ... und } (x_n-\bar{x})^2$$
- Schritt: Nun zählen wir die Quadrate aller Abstände zusammen und berechnen den Durchschnitt (d. h. wir dividieren durch $n$):
- $$\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n}$$
- Da wir oben quadriert haben, ziehen wir nun wieder die Wurzel (Achtung: Dadurch fallen die $(\ )^2$ nicht weg!):
- $$\sqrt{\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n} }$$
Oder verkürzt angeschrieben: $$\sqrt{ \frac{\sum_{i}(x_i-\bar{x})^2}{n} }$$
|
Die Standardabweichung $\sigma$ ist ein Maß für die Abweichung aller Werte vom arithmetischen Mittel $\bar{x}$ und wird berechnet mit
$$\sigma=\sqrt{\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n} }$$ Verkürzt: $$\sigma=\sqrt{ \frac{\sum_{i}(x_i-\bar{x})^2}{n} }$$
|
Berechnen Sie arithmetisches Mittel und Standardabweichung der Liste $\{1;2;2;2;5\}$.
$$\bar{x}=\frac{1+2\cdot 3+5}{5}=\frac{12}{5}=2.4$$ Somit beträgt das arithmetische Mittel $\bar{x}=2.4$.
Um die Standardabweichung zu berechnen, ermitteln wir zuerst die Varianz und ziehen anschließend die Wurzel (so vermeiden wir häufige Rechenfehler):
$$\sigma^2 =\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n}$$
$$\sigma^2=\frac{(1-2.4)^2+(2-2.4)^2+(2-2.4)^2+(2-2.4)^2+(5-2.4)^2}{5}$$
$$\sigma^2=\frac{(1-2.4)^2+(2-2.4)^2\cdot 3+(5-2.4)^2}{5}$$
$$\sigma^2=\frac{(-1.4)^2+(-0.4)^2\cdot 3+2.6^2}{5}$$
$$\sigma^2=\frac{9.2}{5}=1.84$$
Somit erhalten wir für die Standardabweichung $\sigma$:
$$\sigma=\sqrt{\sigma^2}=\sqrt{1.84}=1.36$$
Die Standardabweichung beträgt $\sigma=1.36$.
Quartile
|
Die Quartile $Q_1,\ Q_2\,\ Q_3$ teilen die Werte der Datenmenge insgesamt in $4$ Bereiche.
Berechnung:
|
Die Quartile sind vor allem für die Erstellung eines Boxplot-Diagramms relevant.
Gegeben ist die Datenliste $\{1;2;2;2;5\}$. Bestimme $x_{min},\ x_{max}$ sowie alle Quartile und erstelle damit ein Boxplot-Diagramm.
|
Der Quartilsabstand ist der Abstand zwischen den Quartilen $Q_1$ und $Q_3$.
$$\text{Quartilsabstand}=Q_3-Q_1$$ Graphisch entspricht dies der Länge der „Box“ im Boxplot-Diagramm. |
Gegeben ist die Datenliste $\{1;2;2;2;5\}$. Bestimme den Quartilsabstand der Daten.
Somit beträgt der Quartilsabstand $$Q_3-Q_1=3.5-1.5=2$$
- $Bifie$ : Schiunfälle (leicht)
- Siehe auch Wachstums- und Zerfallsprozesse
- $Bifie$ : Radausflug (mittel-mittel-mittel-leicht)
- Siehe auch
- * Wachstums- und Zerfallsprozesse
- * Trigonometrie
- $Bifie$: Weinbau und Weinkonsum (mittel-mittel-leicht)
- Siehe auch
- $Bifie$: Photovoltaik (2) (leicht)
- Siehe auch
GeoGebra
Ti-8x
Excel
Dieser Bereich ist nur für spezielle Schulformen (z. B. HLW und HAK) relevant.
Die Regression ist eine Methode in der Statistik, den Zusammenhang (= Korrelation) zwischen zwei Merkmalen zu überprüfen.
Einleitung
Sind zwei metrische Merkmale gegeben (z. B. Alter und Verdienst in einer Firma), so kann mithilfe der Regression der Zusammenhang dieser Merkmale überprüft und beschrieben werden.
Zuerst werden die Merkmale in einer Punktwolke dargestellt.
Die Regression versucht nun, den Graphen einer Funktion „möglichst gut“ durch diese Punkte zu legen.
„Möglichst gut“ bedeutet dabei, dass die Summe der Quadrate der $y$-Abstände zwischen Funktion und Punkten so gering wie möglich sein soll.
$Aha!$ $\ $ Dieses Arbeitsblatt zeigt dir die grundlegende Idee am Beispiel einer linearen Regression, bei der die „bestmögliche“ Gerade gesucht ist:
Was bei diesem Applet zu tun ist:
1. Hake das Kästchen „Gerade“ an.
2. Nun kannst du dir die vertikalen Abstände der Punkte zur Geraden und die Abstandsquadrate anzeigen lassen.
3. Verschiebe die blauen Punkte auf der Geraden so, dass die Summe der Abstandsquadrate minimal wird.
4. Wenn du glaubst, du hast nun die beste Gerade entdeckt, klicke auf das Kästchen bei „Trendlinie”. Die Trendlinie ist das Ergebnis der linearen Regression und gibt jene Gerade an, deren Abstandsquadrate minimal sind.
| Idee der Regression |
|---|
|
|
| Falls das Applet nicht angezeigt wird, klicke hier. |
Da wir im Unterricht die Regressionsgleichung immer mithilfe des Technologieeinsatzes lösen, überspringen wir die Herleitung der Regressionsgleichungen.
Regressionsgleichung mithilfe von Technologie berechnen und darstellen
| GeoGebra | Ti-8x |
|---|---|
| Wichtig beim ersten Mal: $\ $ Damit bei der Regression auch der Korrelationskoeffizient angezeigt wird, muss „Diagnostic“ auf „ON“ sein. Dies machst du, indem du auf Folgendes klickst:
$[2nd]+[0]$, dann gehe hinunter zu $DiagnosticOn$ und drücke $2$-mal $[Enter]$. Das Video zeigt dir, wie die Regression mit einer linearen Funktion funktioniert.
|
Lineare Regression
Bei der linearen Regression werden die Daten mithilfe einer linearen Funktion („Gerade“) verbunden.
Musterbeispiel
| Alter (X) | Gehalt (Y) |
|---|---|
| 25 | 1800 |
| 27 | 2500 |
| 28 | 2400 |
| 35 | 3000 |
| 40 | 3000 |
| 40 | 2000 |
| 50 | 3600 |
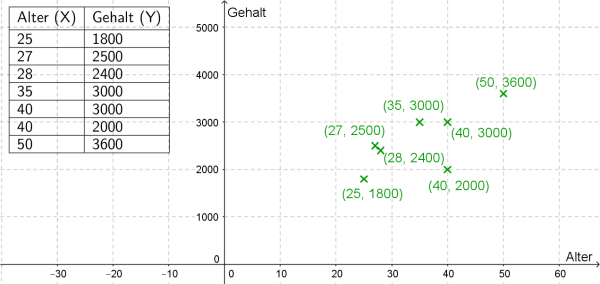
Gegeben ist die folgende Tabelle, die das Alter und Gehalt der Bediensteten in einer Firma angibt.
a) Stellen Sie die Daten in einer Punktwolke dar, wobei das Alter die $x$- und das Gehalt die $y$-Koordinate eines jeden Punktes angeben soll.
b) Ermitteln Sie die Gleichung der Regressionsgeraden und zeichnen Sie diese in die Graphik ein.
c) Berechnen Sie mithilfe der Gleichung der Regressionsgeraden jenes Gehalt, über das eine 45-jährige Person verfügen sollte.
d) Bestimmen Sie mithilfe der Gleichung der Regressionsgeraden jenes Alter, bei dem ein Gehalt von $€4 200$ erreicht werden sollte.
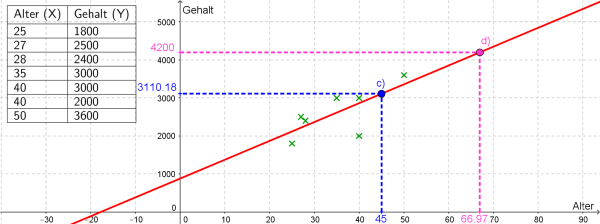
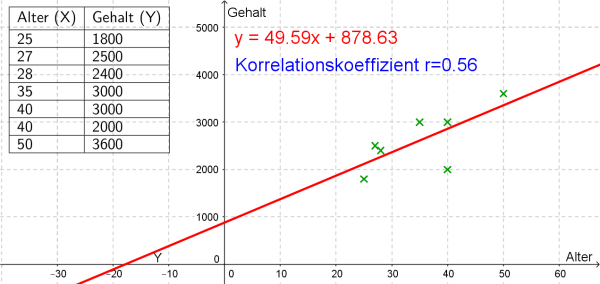
b) Ermitteln Sie die Gleichung der Regressionsgeraden und zeichnen Sie diese in die Graphik ein.
Durch Einsatz von Technologie erhalten wir die Gleichung $$f(x)=49.59x+878.63$$
c) Berechnen Sie mithilfe der Gleichung der Regressionsgeraden jenes Gehalt, über das eine 45-jährige Person verfügen sollte.
Aus der Angabe wissen wir, dass $x=45$. Gesucht ist nun der passende $y$-Wert $y=f(45)$.
$$f(x)=49.59x+878.63$$
$$f(45)=49.59\cdot 45+878.63$$
$$f(45)=3110.18 $$
Bei einem Alter von 45 Jahren ist ein Gehalt von $€3 110.18$ zu erwarten.
d) Bestimmen Sie mithilfe der Gleichung der Regressionsgeraden jenes Alter, bei dem ein Gehalt von $€4 200$.
Gegeben ist die $y$-Korrdinate $y=f(x)=4200$. Gesucht ist nun der $x$-Wert:
$$f(x)=49.59x+878.63$$
$$4200=49.59x+878.63$$
Durch Freistellen von $x$ (siehe Äquivalenzumformungen) erhalten wir
$$x=66.97$$
Bei einem Alter von ca. $67$ Jahren wäre ein Gehalt von $€4 200$ zu erwarten (vorausgesetzt, die Person ist noch nicht in Pension).
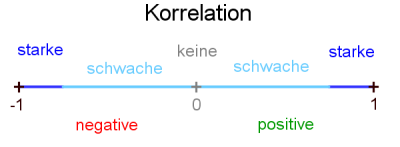
Korrelationskoeffizient $r$
Durch Berechnung der Regressionsgeraden kann noch keine Aussage über die Stärke des Zusammenhangs zweier Merkmale ($X$ und $Y$) ausgesagt werden. Dazu benötigt man den
|
Korrelationskoeffizient $r$
Der Korrelationskoeffizient $r$ gibt an, wie stark zwei Merkmale $X$ und $Y$ zusammenhängen.
|
$Aha!$ $\ $ In folgendem GeoGebra-Applet lernst du, wie die Korrelation durch die Lage der Punkte verändert wird.
Wie dieses Applet funktioniert:
Verschiebe die grünen Punkte (Datenpunkte), so dass
a) ein starker positiver Zusammenhang (d. h. $r\approx 1$),
b) ein starker negativer Zusammenhang (d. h. $r\approx -1$),
c) ein schwacher negativer Zusammenhang (d. h. $0.3\leq r\leq 0$) oder
d) kein Zusammenhang (d. h. $r=0$)
herrscht.
| Übung zum Korrelationskoeffizient |
|---|
|
|
| Falls das Applet nicht angezeigt wird, klicke hier. |
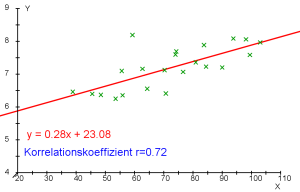
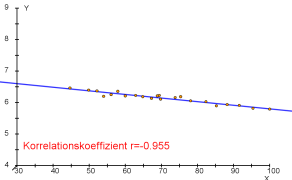
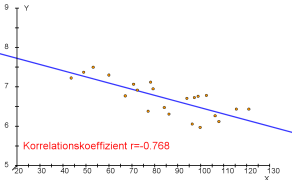
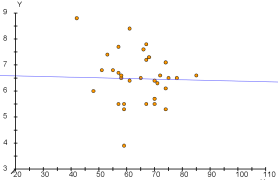
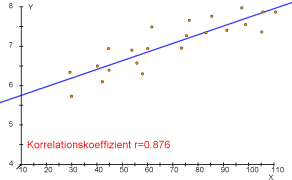
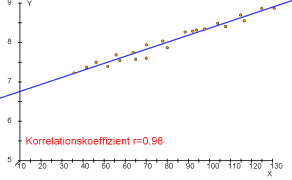
- Beispiele für Punktwolken und dazugehörende Korrelationskoeffizienten.
Korrelation und Kausalität
|
Eine starke Korrelation (d. h. $\vert r\vert$ nahe bei 1) bedeutet noch lange nicht, dass es auch einen ursächlichen Zusammenhang zwischen zwei Merkmalen gibt. Oft spielen z. B. noch viel mehr Einflüsse eine Rolle. |
Beispiele für Korrelation aber (wahrscheinlich) keinen direkten ursächlichen Zusammenhang:
- Die Größe der Bevölkerung ($X$) hat Auswirkungen auf die Geschwindigkeit der Plattentektonik ($Y$).
- Je mehr Menschen auf einer Kontinentalplatte leben, desto schneller bewegt sich diese. Beispiele: Indien, Japan.
- Ein Rückgang an Störchen führt zu einer Abnahme an Neugeburten (Quelle).
- Tatsächlich spielt hier eine dritte Variable, nämlich die Verstädterung einer Region eine Rolle.
Matura-Aufgaben
|
Schrittfolge zur Berechnung von Regressionsaufgaben
|
$Bifie$: Schotterwerk (leicht-mittel-mittel)
siehe auch
$Bifie$: Reisekosten (leicht-leicht-schwer-leicht)
siehe auch
$Bifie$: Preis und Absatz (mittel)
siehe auch
$Bifie$: Hustensaft (mittel-mittel-leicht)
siehe auch
$Bifie$: Intelligenzquotient (leicht-leicht-leicht)
siehe auch
$Bifie$: Kängurusprünge (leicht-mittel-leicht)
siehe auch
$Bifie$: Elektronikhersteller (mittel-schwer-leicht)
siehe auch
$Bifie$: Sektkellerei (mittel-leicht-schwer)
siehe auch
$Bifie$: Fahrzeugtests (2) (mittel)
siehe auch
$Bifie$: CeBit (2) ((leicht-mittel-mittel)
siehe auch
$Bifie$: Jahresumsatz ((leicht-leicht-mittel)
siehe auch
- Beschreibende Statistik
- Gleichungssysteme (2.7.)
$Bifie$: Kostenanalyse (leicht-mittel-leicht)
siehe auch
$Bifie$: Urlaubsreisen (mittel-leicht-leicht)
siehe auch