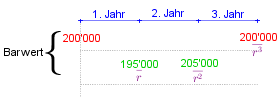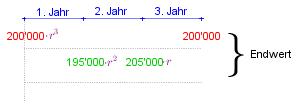Äquivalenzprinzip (Vergleich von Einzahlungen)

Das Äquivalenzprinzip ist wichtig, wenn Einzahlungen, die zu verschiedenen Zeitpunkten getätigt werden, verglichen werden müssen.

Definition

Das Äquivalenzprinzip der Finanzmathematik besagt:

'"Zahlungen dürfen nur dann verglichen/addiert/subtrahiert werden, wenn sie zuvor auf denselben Stichtag auf- oder abgezinst wurden." '

Musterbeispiel

Für ein Grundstück erhält Elizabeth Reichgut zwei Angebote für ein zum Verkauf stehendes Grundstück:

Andreas Ohneland (A) bezahlt € 200'000 sofort und € 200'000 nach 3 Jahren.
Bernhard Grundlos (B) bezahlt € 195'000 nach einem Jahr und € 205'000 nach zwei Jahren.

Frage: Für weches Angebot soll sie sich entscheiden, wenn von einem Zinssatz von $i_{eff}=4$% p.a. ausgangen werden kann?

Antwort: Auf den ersten Blick wirken beide Angebote gleich gut, da beide insgesamt € 400'000 überweisen. Allerdings kommen nicht alle Einzahlungen zum selben Zeitpunkt, weswegen sie auch anders verzinst werden.

In der Abbildung sind die Zahlungen an einem Zahlenstrahl angeordet

Laut dem Äquivalenzprinzip müssen wir die Einzahlungen zuerst auf denselben Stichtag auf- oder abzinsen, um sie zu vergleichen. Hier gibt es zwei sinnvolle Möglichkeiten:

Abzinsen auf den Beginn (Berechnung des Barwertes $B$)
Aufzinsen auf das 3. Jahr (Berechnung des Endwertes $E$)

Der Aufzinungsfaktor r beträgt $r=1.04$ (da $i_{eff}=4$ und $r=1+\frac{i_{eff}}{100}$ )

Zur Verdeutlichung wird bei diesem Beispiel sowohl der Barwert, als auch der Endwert berechnet. Selbstverständlich würde es reichen, wenn nur eines von beiden berechnet wird:

Berechnung des Barwerts

Berechnung des Endwerts

Wir zinsen alle Einzahlungen zum Beginn ab (d.h. dividieren mit dem Abzinsungsfaktor):

Berechnung des Barwertes

Angebot A: $B_A=200000+\frac{200000}{r^3}=377'799,27$
Angebot B: $B_B=\frac{195000}{r}+\frac{205000}{r^2}=377'034,02$

Antwort Somit ist das Angebot A besser für Elizabeth (da es höher ist).

Wir zinsen alle Einzahlungen zum Ende auf (d.h. multiplizieren mit dem Aufzinsungsfaktor):

Berechnung des Endwertes

Angebot A: $E_A=200000\cdot r^3+200000=424'972,80 $
Angebot B: $E_B=195000\cdot r^2+205000\cdot r=424'112,00 $

Antwort Somit ist das Angebot A besser für Elizabeth (da es höher ist).

In beiden Fällen (sowohl beim Barwert, als auch beim Endwert) ist das Angebot A besser!

Merke

Beim Äquivalenzprinzip ist es egal, ob du den Barwert oder den Endwert berechnest oder gar auf einen anderen Stichtag verzinst. Das bessere Angebot wird jedesmal besser sein, zu jedem Zeitpunkt!

Maturabeispiele

1. Für ein Grundstück werden zwei Angebote vorgelegt:

A: 50‘000 sofort, 30‘000 nach 7 Jahren.

B: 40‘000 nach 3 Jahren und 45‘000 nach 6 Jahren.

a) Berechne, welches Angebot bei einer Verzinsung von 2% p.a. besser ist.

Lösung durch Berechnung des Endwertes $E_7$:

$r=1+\frac{2}{100}=1.02$

A: $50000\cdot r^7 + 30000=87‘434.28$

B: $40000\cdot r^4+45000\cdot r= 89‘197.28$

Antwort: Angebot B ist bei einer Verzinsung von 2% somit besser.

b) Berechne, welches Angebot bei einer Verzinsung von 4% p.a. besser ist.

Lösung durch Berechnung des Endwertes $E_7$:

$r=1+\frac{4}{100}=1.04$

A: $50000\cdot r^7 + 30000=95‘796.59$

B: $40000\cdot r^4+45000\cdot r= 93‘594.34$

Antwort: Angebot A ist bei einer Verzinsung von 4% besser.

c) Berechne, bei welchem Zinssatz beide Angebote gleichwertig sind.

Lösung:

Hier muss Berechnet werden, wann ist $$\textrm{Wert von Angebot A}=\textrm{Wert von Angebot B}$$ $$ 50000\cdot r^7 + 30000 = 40000\cdot r^4+45000\cdot r $$

Nun muss r berechnet werden. Diese Gleichung löst man am besten mit dem Solve-Befehl, wo wir annehmen können, dass $r$ zwischen 1.02 und 1.04 liegt (siehe Lösungen a) und b) ).

Man erhält: $r=1.0294$ und somit ist $i=2.94$%.

Antwort: Bei einem Zinssatz von 2.94% sind beide Angebote gleichwertig.