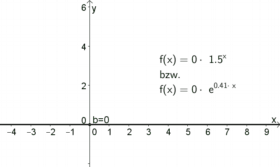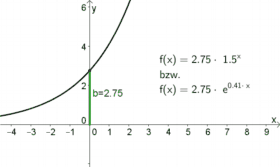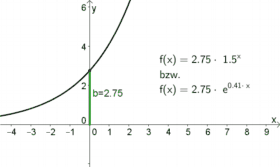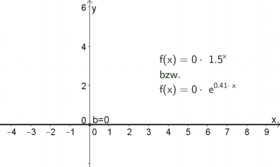Exponentialfunktionen: Unterschied zwischen den Versionen
(→Graph der Exponentialfunktion) |
(→Weitere Eigenschaften der Exponentialfunktion) |
||
| Zeile 67: | Zeile 67: | ||
* Die $x$-Achse ist eine [[Asymptote]] des Graphen. D. h. der Graph der Exponentialfunktion nähert sich dieser beliebig nahe, ohne sie jemals zu schneiden. | * Die $x$-Achse ist eine [[Asymptote]] des Graphen. D. h. der Graph der Exponentialfunktion nähert sich dieser beliebig nahe, ohne sie jemals zu schneiden. | ||
| − | * Die Exponentialfunktion hat die besondere Eigenschaft, dass sie sich in bestimmten Abständen immer um | + | * Die Exponentialfunktion hat die besondere Eigenschaft, dass sie sich in bestimmten Abständen immer um „denselben Faktor“ vermehrt (wenn $a>1$) oder vermindert (wenn $0<a<1$) $\rightarrow $ siehe Abbildungen unten. Formal gilt: |
$$f(x+1)=f(x)\cdot a\ \ \textrm{ bzw. }\ \ \ \frac{f(x+1)}{f(x)}=a$$ | $$f(x+1)=f(x)\cdot a\ \ \textrm{ bzw. }\ \ \ \frac{f(x+1)}{f(x)}=a$$ | ||
* Aufgrund der letzten Eigenschaft werden Exponentialfunktionen für die Beschreibung von Wachstumsprozessen (z. B. Wachstum einer Bakterienpopulation) oder Zerfallsprozessen (z. B. Zerfall eines radioaktiven Elements) verwendet. | * Aufgrund der letzten Eigenschaft werden Exponentialfunktionen für die Beschreibung von Wachstumsprozessen (z. B. Wachstum einer Bakterienpopulation) oder Zerfallsprozessen (z. B. Zerfall eines radioaktiven Elements) verwendet. | ||
Version vom 27. Dezember 2018, 19:40 Uhr
Diese Seite behandelt grundlegende Eigenschaften der Exponentialfunktion. Die Anwendungsbeispiele findest du auf der Seite Wachstums- und Zerfallsprozesse.
|
Exponentialfunktionen sind Funktionen, deren Funktionsgleichung die Form
$$f(x)=b\cdot a^x \textrm{ mit } a, b \in \mathbb{R}^+$$ oder $$ f(x)=b\cdot e^{\lambda \cdot x} \textrm{ mit } b \in \mathbb{R}^+,\ \lambda \in \mathbb{R} $$ |
Hinweise
- In Exponentialfunktionen steht die Variable immer im Exponenten
- Im Term $a^x$ ist $a$ die Basis
- $e$ steht für die Eulersche Zahl
- $a=e^\lambda \rightarrow$ Dies ist der Zusammenhang der beiden Funktionsgleichungen
- $\lambda$ ist der griechische Buchstabe Lambda
Inhaltsverzeichnis
Graph der Exponentialfunktion
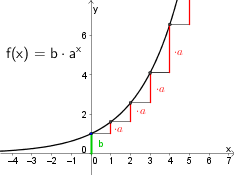
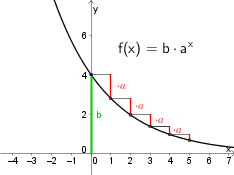
Je nach Größe der Parameter $a$ und $b$ bzw. $\lambda$ verändert sich der Graph. Im Folgenden werden die Auswirkungen der einzelnen Parameter auf den Graphen der Funktion besprochen:
$$f(x)=b\cdot a^x \ \ \ \textrm{ bzw.}\ \ \ f(x)=b\cdot e^{\lambda\cdot x}$$
| $b$ gibt den Schnittpunkt mit der $y$-Achse an.
Begründung: Beim Schnittpunkt mit der $y$-Achse ist die $x$-Koordinate gleich $0$. Die dazugehörige $y$-Koordinate erhält man dann durch: $f(0)=b\cdot a^0 =b\cdot 1=b$ (mit der $e^\lambda$-Formel funktioniert es genauso) |
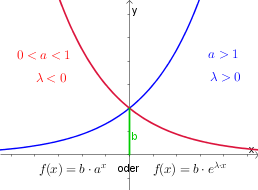
| $a$ und $\lambda$ geben an, ob der Graph steigt oder fällt. | ||
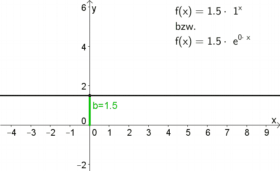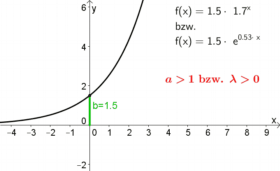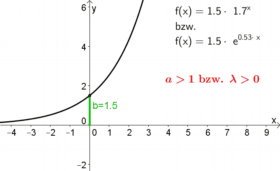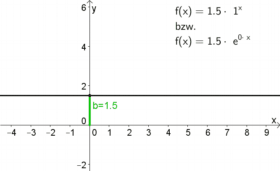
| Für $a>1$ oder $\lambda>0$ |
ist der Graph monoton steigend. Je größer $a$ bzw. $\lambda$ ist, desto stärker steigt der Graph. |
|
| Für $0<a<1$ oder $\lambda<0$ | ist der Graph monoton fallend und nähert sich immer mehr der $x$-Achse. | 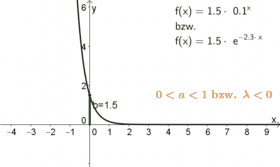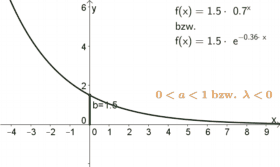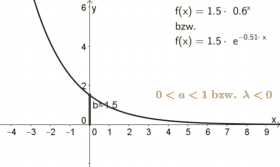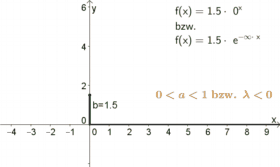
|
- $Aha!$ : In diesem Arbeitsblatt kannst du noch einmal die obigen Schritte nachvollziehen (Achtung: Anstelle von "$b$" wurde hier der Buchstabe "$c$" verwendet!)
- ? : Hier findest du ein Quiz, in dem du das Gelernte überprüfen kannst.
Weitere Eigenschaften der Exponentialfunktion
- Die $x$-Achse ist eine Asymptote des Graphen. D. h. der Graph der Exponentialfunktion nähert sich dieser beliebig nahe, ohne sie jemals zu schneiden.
- Die Exponentialfunktion hat die besondere Eigenschaft, dass sie sich in bestimmten Abständen immer um „denselben Faktor“ vermehrt (wenn $a>1$) oder vermindert (wenn $0<a<1$) $\rightarrow $ siehe Abbildungen unten. Formal gilt:
$$f(x+1)=f(x)\cdot a\ \ \textrm{ bzw. }\ \ \ \frac{f(x+1)}{f(x)}=a$$
- Aufgrund der letzten Eigenschaft werden Exponentialfunktionen für die Beschreibung von Wachstumsprozessen (z. B. Wachstum einer Bakterienpopulation) oder Zerfallsprozessen (z. B. Zerfall eines radioaktiven Elements) verwendet.
Beispiele zur Bestimmung der Funktionsgleichung
Allgemeiner Lösungsweg: Die Funktionsgleichung wird bestimmt, indem man $2$ Punkte auf dem Funktionsgraphen bestimmt und diese dann in die Funktionsgleichung einsetzt. Am einfachsten ist es, wenn einer der Punkte der Schnittpunkt des Graphen mit der $y$-Achse ist, da so b einfach bestimmt werden kann.
1. Beispiel mit $f(x)=b\cdot a^x$ (einfach)
Angabe: Die Exponentialfunktion $f(x)=b\cdot a^x$ geht durch die Punkte $(0|3)$ und $(2|12)$. Bestimme die Parameter $a$ und $b$.
Lösung:
Um $a$ und $b$ zu bestimmen, setzen wir die Punkte in die Funktionsgleichung ein:
|
$\ \ \ \ \ y=b\cdot a^x$
$\rightarrow 3=b\cdot a^0\ \ \ \ \ \rightarrow \underline{3=b}\ \ $ (Hinweis: Da f bei (0|3) die y-Achse schneidet, hätten wir schon vorher gewusst, dass $b=3$ ist.) $\rightarrow 12=3\cdot a^2 \ \ \ \rightarrow 4=a^2 \rightarrow \underline{a=2}$ |
Somit gilt: $\underline{\underline{f(x)=3\cdot 2^x }}$
2. Beispiel mit $f(x)=b\cdot a^x$ (mittel)
Angabe: Die Exponentialfunktion $f(x)=b\cdot a^x$ geht durch die Punkte (1|4) und (2|16) bestimme die Parameter a und b.
Lösung:
Um a und b zu bestimmen, setzen wir die Punkte in die Funktonsgleichung ein:
|
$\ \ \ \ \ y=b\cdot a^x$
$\rightarrow I:\ 4=b\cdot a^1$ $\ \rightarrow II: 16=b\cdot a^2$ |
|---|
Hier haben wir nun ein Gleichungssystem mit 2 Gleichungen und zwei Unbekannten. Dieses können wir mithilfe des Einsetzungsverfahrens lösen: Hierzu stellen wir in I die Unbekannte $a$ frei: $I:\ 4=b\cdot a^1 \ \ \rightarrow a=$ $\frac{4}{b}$ und setzen dies nun in II ein:
$II:\ 16=b\cdot ($ $\frac{4}{b}$ $)^2$ $$II:\ 16=b\cdot (\frac{4}{b})^2$$ $$II: \ 16=b\cdot (\frac{16}{b^2})\ \ \ |\cdot 16$$ $$II: \ 16\cdot b^2 = 16 \ \ \ |:16 $$ $$II: \ b^2=1 $$ $$II: \ b=\pm 1$$ Da laut der Definition (ganz oben) $b>0$ ist, muss gelten $\underline{b=1}$
Damit erhalten wir $a=\frac{4}{b} \rightarrow \underline{a=4}$
Antwort: Somit lautet die Funktionsgleichung $\underline{\underline{f(x)=1\cdot 4^x}}$ bzw. $\underline{\underline{f(x)=4^x}}$
3. Beispiel mit $f(x)=b\cdot e^{\lambda \cdot x}$ (einfach)
Die Exponentialfunktion $f(x)=b\cdot e^{\lambda \cdot x}$ geht durch die Punkte (0|3) und (2|27). Bestimme die Parameter $\lambda$ und b
Lösung:
1. Punkt (0|3): Da der Graph die y-Achse hier schneidet, muss gelten $\underline{b=3}$ (siehe oben Beispiel 1)
2. Punkt (2|27): Wir setzen diesen Punkt und b=3 nun in die Funktionsgleichung, um $\lambda$ zu erhalten: $$f(x)=b\cdot e^{\lambda \cdot x}$$ $$27=3\cdot e^{\lambda \cdot 2}$$ Nun wenden wir den Logarithmus an: $$9=e^{\lambda \cdot 2} \ \ \ | \ln(\ )$$ $$\ln(9)=\ln(e^{\lambda \cdot 2})$$ $$\ln(9)=\lambda \cdot 2\cdot \ln(e) \ \ \ |ln(e)=1 \ \ |:2$$ $$\frac{ln(9)}{2}=\lambda$$ $$\underline{1.1=\lambda}$$
Somit lautet die Funktionsgleichung $\underline{\underline{f(x)=3\cdot e^{1.1\cdot x}}}$
Weitere Übungen
Bestimme die Funktionsgleichung in der Form $f(x)=b\cdot a^x$. Gib dazu die Funktionsgleichung bei $f(x)=$ ein.
- ? : Kannst du alle Aufgaben von oben, so übe dich an diesem Quiz, in dem du die Funktionsgleichung verschiedener Funktionstypen bestimmen musst.
Beispiel zur Bestimmung von Funktonswert und Argument
1. Beispiel mit $f(x)=b\cdot e^{\lambda\cdot x}$ (leicht)
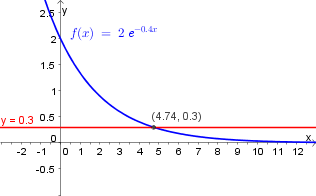
Gegeben ist die Funktion $f(x)=2\cdot e^{-0.4\cdot x}$. Bestimme jene Argumente für die gilt
- a) $f(x)=0.3$
- b) $f(x)=0$
- c) $f(x)=-0.5$
Lösung:
Lösung für a)
Es gilt die Gleichung $f(x)=0.3$ zu lösen, wobei $f(x)=2\cdot e^{-0.4\cdot x}$ ist: $$2\cdot e^{-0.4\cdot x}=0.3$$ $$ e^{-0.4\cdot x}=\frac{0.3}{2} \ \ \ \ | ln()$$ $$ -0.4\cdot x \cdot \ln(e)=\ln(\frac{0.3}{2})\ \ \ \ |ln(e)=1 \ \ \ |:(-0.4) $$ $$x=\frac{\ln(\frac{0.3}{2})}{-0.4}$$ $$\underline{\underline{x = 4.74}}$$ Alternative Lösungswege:
- Graphisch den Schnittpunkt zwischen f(x) und y=0.3 ermitteln (siehe Abbildung rechts)
- Solve-Befehl im TR oder Löse-Befehl mit GeoGebra
Lösung für b)
Da die x-Achse des Graphen von f(x) eine Asymptote ist, hat f(x) keine Nullstellen und somit gibt es kein x für das gilt $f(x)=0$ Alternativer Lösungsweg:
- Löse-Befehl mit GeoGebra $\rightarrow$ als Lösung erhält man die leere Menge $\mathbb{L}=\{ \}$
- Rechnerisch:
$$ f(x)=0$$ $$2\cdot e^{-0.4\cdot x}=0 \ \ \ |:2$$ $$ e^{-0.4\cdot x}=0 \ \ \ |ln $$ $$ -0.4\cdot x\cdot \ln(e)=\ln(0)$$ Da der Logarithmus nur für positive x-Werte definiert ist ($\mathbb{D}=\mathbb{R}^+$), ist $\ln(0)$ nicht definiert (was du leicht im TR mit der Rechnung ln(0) überprüfen kannst). Somit hat die Gleichung $ -0.4\cdot x\cdot \ln(e)=\ln(0)$ keine Lösung.
Lösung für c)
Auch hier gibt es keine Lösung, da der Wertebereich der Exponentialfunktion $2\cdot e^{-0.4\cdot x}$ oberhalb der x-Achse liegt und $f(x)$ somit niemals negative Funktionswerte annimmt. (Siehe Abbildung bei Lösung a)
2. Beispiel mit $f(x)=b\cdot a^x$ (leicht)
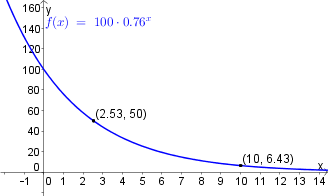
Gegeben ist die Funktion $f(x)=100\cdot 0.76^x$.
- a) Bestimme wie groß ist der Funktionwert an der Stelle $x=5$ ist.
- b) Berechne, an welcher Stelle die Funktion einen Wert von $50$ hat.
- c) Fertige eine Skizze des Graphen und zeichnen Sie die berechneten Werte ein.
Lösung:
Lösung a) $$f(5)=100\cdot 0.76^5=25.36 $$
Lösung für b) $$f(x)=50\ \ \ \ |textrm{gesucht ist x}$$ $$100\cdot 0.76^x=50\ \ \ |:100$$ $$0.75^x=0.5\ \ \ |\log(\ )$$ $$\log 0.75^x= \log 0.5$$ $$x\cdot \log 0.75=\log 0.5$$ $$x=\frac{\log 0.5}{\log 0.75}$$ $$\underline{\underline{x=2.53}}$$ Hinweis: In der obigen Rechnung wurde der Logarithmus verwendet.
Lösung c) Siehe Abbildung rechts
Interaktives Quiz
Weitere Materialien
- $Step\ by\ Step!$ : Ein Online-Lernpfad von G. Jauck und A. Lindner
- ? : Ein Quiz in dem du den Graph und die Funktionsgleichung zusammenführen musst
- ? : Und hier gibt es ein GeoGebraquiz, in dem du die Funktionsgleichung verschiedener Funktionstypen bestimmen musst.
Matura-Aufgaben
- $Bifie$ : Mount Everest (bifie-Aufgabe: leicht-mittel-schwer)
- Siehe auch Logarithmus
- $Bifie$ : Vergessenskurve von Ebbinghaus (bifie-Aufgabe: leicht-mittel-mittel)
- $Bifie$ : Bevölkerung der USA (leicht-leicht-mittel)
- Siehe für Aufgabe b) und c) auch Differenzen- und Differentialquotient