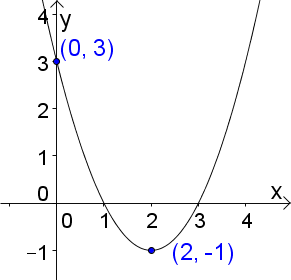Quadratische Funktionen: Unterschied zwischen den Versionen
Aus Matura Wiki
| Zeile 3: | Zeile 3: | ||
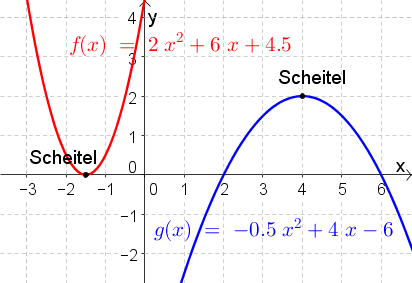
{{Vorlage:Definition|1=Die Funktionsgleichung einer quadratischen [[Funktionen|Funktion]] (auch [[Potenz- und Polynomfunktionen|Polynomfunktion]] 2. [[Grades]] genannt) lautet $$y=a\cdot x^2+b\cdot x+c$$ | {{Vorlage:Definition|1=Die Funktionsgleichung einer quadratischen [[Funktionen|Funktion]] (auch [[Potenz- und Polynomfunktionen|Polynomfunktion]] 2. [[Grades]] genannt) lautet $$y=a\cdot x^2+b\cdot x+c$$ | ||
| − | mit $a,b,c\in$ [[Theorie Zahlenmengen (1.1.)| $\mathbb{R} $ ]] und $a\neq 0$. | + | mit $a,b,c\in$ [[Theorie Zahlenmengen (1.1.)| $\mathbb{R} $ ]] und $a\neq 0$.}} |
| Zeile 12: | Zeile 12: | ||
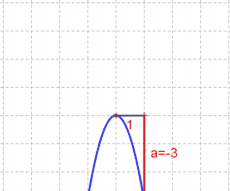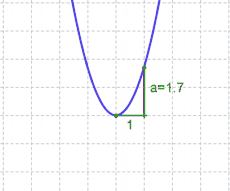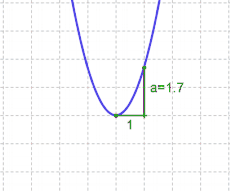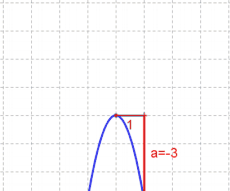
* <span style="background-color:#00FFFF">!Wichtig! </span> Der Graph einer quadratischen Funktion ist IMMER eine '''Parabel''' und damit $\cup$- oder $\cap$-förmig (siehe Abbildungen rechts). | * <span style="background-color:#00FFFF">!Wichtig! </span> Der Graph einer quadratischen Funktion ist IMMER eine '''Parabel''' und damit $\cup$- oder $\cap$-förmig (siehe Abbildungen rechts). | ||
| − | * Quadratische Funktionen haben immer genau einen [[Extremstellen | Hoch- oder Tiefpunkt]]. Diesen nennt man '''Scheitelpunkt''' (oder '''Scheitel''') | + | * Quadratische Funktionen haben immer genau einen [[Extremstellen | Hoch- oder Tiefpunkt]]. Diesen nennt man '''Scheitelpunkt''' (oder kurz '''Scheitel'''). |
* Die Gleichung $ y=a\cdot x^2+b\cdot x+c$ wird als '''Normalform''' bezeichnet (sozusagen: ''im Normalfall ist die Funktion in dieser Form gegeben''). | * Die Gleichung $ y=a\cdot x^2+b\cdot x+c$ wird als '''Normalform''' bezeichnet (sozusagen: ''im Normalfall ist die Funktion in dieser Form gegeben''). | ||
| Zeile 50: | Zeile 50: | ||
{| style="background-color:#D3D3D3" | {| style="background-color:#D3D3D3" | ||
| − | |'''Achtung:''' Im Gegensatz zu den [[lineare Funktionen | linearen Funktionen]] darf man hier immer nur 1 nach rechts, niemals mehr. Der Grund: Die Steigung der Parabel ändert sich, sie wird immer steiler. Dagegen ist die Steigung der Linearen Funktion immer konstant. | + | |'''Achtung:''' Im Gegensatz zu den [[lineare Funktionen | linearen Funktionen]] darf man hier immer nur $1$ nach rechts, niemals mehr. Der Grund: Die Steigung der Parabel ändert sich, sie wird immer steiler. Dagegen ist die Steigung der Linearen Funktion immer konstant. |
| − | Allgemein gilt: Ist eine Steigung konstant, so ist es egal, ob man z.B. 1 nach rechts und 3 hinauf, oder 2 nach rechts und 6 hinauf geht. | + | Allgemein gilt: Ist eine Steigung konstant, so ist es egal, ob man z. B. $1$ nach rechts und $3$ hinauf, oder $2$ nach rechts und $6$ hinauf geht. |
|} | |} | ||
| Zeile 65: | Zeile 65: | ||
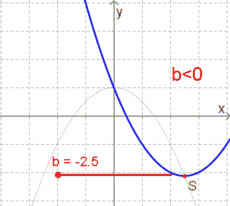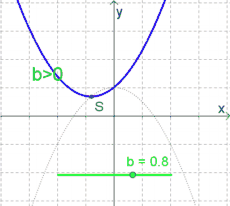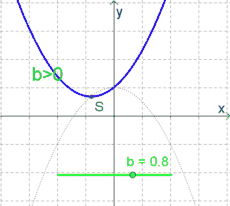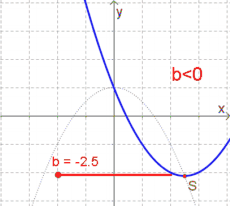
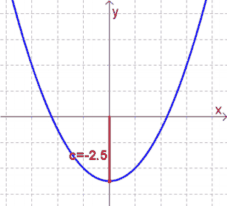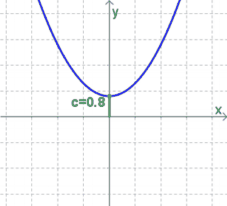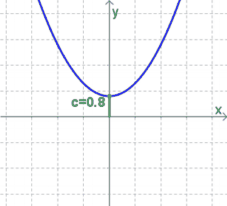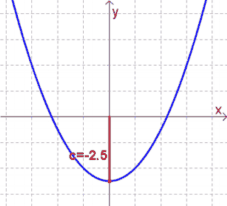
Ist $a>0$, so gilt: | Ist $a>0$, so gilt: | ||
| − | * Ist $b<0$, so liegt der Scheitelpunkt '''rechts''' (!) der y-Achse. | + | * Ist $b<0$, so liegt der Scheitelpunkt '''rechts''' (!) der $y$-Achse. |
| − | * Ist $b>0$, so liegt der Scheitelpunkt '''links''' (!) der y-Achse. | + | * Ist $b>0$, so liegt der Scheitelpunkt '''links''' (!) der $y$-Achse. |
| − | * Ist $b=0$, so liegt der Scheitelpunkt genau auf der y-Achse. Der Funktionsgraph ist dadurch symmetrisch zur y-Achse. | + | * Ist $b=0$, so liegt der Scheitelpunkt genau auf der $y$-Achse. Der Funktionsgraph ist dadurch symmetrisch zur $y$-Achse. |
| − | Ist dagegen $a<0$, so bewirkt $b<0$ eine Verschiebung nach '''links''' und $b>0$ eine Verschiebung nach | + | Ist dagegen $a<0$, so bewirkt $b<0$ eine Verschiebung nach '''links''' und $b>0$ eine Verschiebung nach rechts (also genau umgekehrt zu $a>0$)! |
| − | ''' | + | '''Merke:''' |
Für $a>0$: | Für $a>0$: | ||
* $b<0\rightarrow$ rechts | * $b<0\rightarrow$ rechts | ||
| Zeile 84: | Zeile 84: | ||
<span style="color:#A020F0> '''Zusatz für Interessierte''' </span> | <span style="color:#A020F0> '''Zusatz für Interessierte''' </span> | ||
| − | <div class="mw-collapsible-content"> Die Kurve, entlang derer die Parabel verschoben wird, ist die Spiegelung der Parabel parallel zur x-Achse. | + | <div class="mw-collapsible-content"> Die Kurve, entlang derer die Parabel verschoben wird, ist die Spiegelung der Parabel parallel zur $x$-Achse. |
| − | Wer | + | Wer selbstständig beweisen kann, warum dies so ist, dem ist der 1er so gut wie sicher. |
</div> | </div> | ||
| Zeile 97: | Zeile 97: | ||
| − | $c$ gibt den Schnittpunkt mit der y-Achse an (vgl. das [[Lineare Funktionen#d = Abstand auf der y-Achse ("Ordinatenabschnitt") |d bei den linearen Funktionen]]). | + | $c$ gibt den Schnittpunkt mit der $y$-Achse an (vgl. das [[Lineare Funktionen#d = Abstand auf der y-Achse ("Ordinatenabschnitt") |$d$ bei den linearen Funktionen]]). |
| − | * Ist $c>0$, so liegt der Schnittpunkt oberhalb der x-Achse. | + | * Ist $c>0$, so liegt der Schnittpunkt oberhalb der $x$-Achse. |
| − | * Ist $c=0$, so geht die Parabel durch den | + | * Ist $c=0$, so geht die Parabel durch den Koordinatenursprung. |
| − | * Ist $c<0$, so schneidet die Parabel die y-Achse unterhalb der x-Achse. | + | * Ist $c<0$, so schneidet die Parabel die $y$-Achse unterhalb der $x$-Achse. |
| − | |||
| − | |||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 121: | Zeile 119: | ||
== Nullstellen quadratischer Funktionen == | == Nullstellen quadratischer Funktionen == | ||
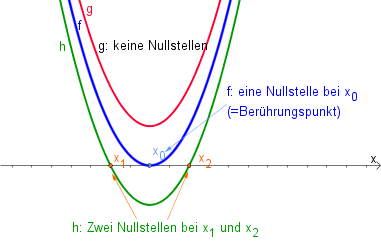
| − | [[Datei:Nullstellen.png|thumb|right|400px| Parabeln mit 0, 1 oder 2 Nullstellen]] | + | [[Datei:Nullstellen.png|thumb|right|400px| Parabeln mit $0, 1$ oder $2$ Nullstellen]] |
| − | Die [[Nullstelle | Nullstellen]] einer quadratischen Funktion sind die Schnittpunkte der Parabel mit der x-Achse. | + | Die [[Nullstelle | Nullstellen]] einer quadratischen Funktion sind die Schnittpunkte der Parabel mit der $x$-Achse. |
Je nachdem, wie die Parabel im Koordinatensystem liegt gibt es: | Je nachdem, wie die Parabel im Koordinatensystem liegt gibt es: | ||
| − | * 2 Nullstellen | + | * $2$ Nullstellen |
| − | * 1 Nullstelle (=Scheitelpunkt liegt auf der x-Achse) | + | * $1$ Nullstelle ($=$ Scheitelpunkt liegt auf der $x$-Achse) |
| − | * 0 Nullstellen. | + | * $0$ Nullstellen. |
| Zeile 134: | Zeile 132: | ||
| − | + | siehe auch [[Quadratische Gleichungen]] | |
| Zeile 142: | Zeile 140: | ||
|2= | |2= | ||
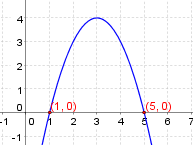
| − | Zuerst setzen wir f(x)=0: | + | Zuerst setzen wir $f(x)=0$: |
$$0=-x^2 + 6 \cdot x - 5$$ | $$0=-x^2 + 6 \cdot x - 5$$ | ||
| − | Nun verwenden wir ein Lösungsverfahren, um die [[Quadratische Gleichungen|quadratische Gleichung]] zu lösen. Hier als Beispiel verwenden wir [[quadratische Gleichungen#die große Lösungsformel | große Lösungsformel]] mit a=-1, b=6 und c=-5 | + | Nun verwenden wir ein Lösungsverfahren, um die [[Quadratische Gleichungen|quadratische Gleichung]] zu lösen. Hier als Beispiel verwenden wir [[quadratische Gleichungen#die große Lösungsformel | große Lösungsformel]] mit $a=-1$, $b=6$ und $c=-5$ |
$$ x_{1,2}=\frac{-b \pm \sqrt{b^2-4\cdot a\cdot c} }{2\cdot a}$$ | $$ x_{1,2}=\frac{-b \pm \sqrt{b^2-4\cdot a\cdot c} }{2\cdot a}$$ | ||
[[Datei:Quadfkt-nullstelle.png|thumb|right|200px]] | [[Datei:Quadfkt-nullstelle.png|thumb|right|200px]] | ||
| Zeile 151: | Zeile 149: | ||
$$ x_1=\frac{-6+4}{-2}=1$$ | $$ x_1=\frac{-6+4}{-2}=1$$ | ||
$$ x_2=\frac{-6-4}{-2}=5$$ | $$ x_2=\frac{-6-4}{-2}=5$$ | ||
| − | '''Antwort:''' Der Graph der Funktion schneidet bei $N_1(1\vert 0)$ und $N_2(5\vert 0)$ die x-Achse. | + | '''Antwort:''' Der Graph der Funktion schneidet bei $N_1(1\vert 0)$ und $N_2(5\vert 0)$ die $x$-Achse. |
}} | }} | ||
<br> | <br> | ||
<br> | <br> | ||
| − | |||
| − | |||
{| align="right" | {| align="right" | ||
| <div class="testbutton-blue"> {{#switchtablink:Rechenbeispiel|$\rightarrow$ nächste Seite ...}} </div> | | <div class="testbutton-blue"> {{#switchtablink:Rechenbeispiel|$\rightarrow$ nächste Seite ...}} </div> | ||
| Zeile 164: | Zeile 160: | ||
=Rechenbeispiel= | =Rechenbeispiel= | ||
== Typische Rechenbeispiele bei gegebener Funktionsgleichung == | == Typische Rechenbeispiele bei gegebener Funktionsgleichung == | ||
| − | {{Vorlage:Beispiel|1=Ein Ball wird in die Höhe geworfen. Die Funktion $h(t)=-0.1t^2+0.3t+3$ gibt die Höhe des Balles in Metern (m) nach t Sekunden (s) an. | + | {{Vorlage:Beispiel|1=Ein Ball wird in die Höhe geworfen. Die Funktion $h(t)=-0.1t^2+0.3t+3$ gibt die Höhe des Balles in Metern ($m$) nach $t$ Sekunden ($s$) an. |
| − | + | ||
<br> | <br> | ||
<br> | <br> | ||
a) Bestimmen Sie die Abwurfhöhe des Balles. | a) Bestimmen Sie die Abwurfhöhe des Balles. | ||
<br> | <br> | ||
| − | b) Ermitteln Sie die Höhe des Balles nach 6 Sekunden. | + | b) Ermitteln Sie die Höhe des Balles nach $6$ Sekunden. |
<br> | <br> | ||
c) Berechnen Sie, zu welchem Zeitpunkt der Ball auf dem Boden aufkommt. | c) Berechnen Sie, zu welchem Zeitpunkt der Ball auf dem Boden aufkommt. | ||
<br> | <br> | ||
| − | d) Ermitteln Sie, zu welchem Zeitpunkt der Ball eine Höhe von 2 m hat. | + | d) Ermitteln Sie, zu welchem Zeitpunkt der Ball eine Höhe von $2 m$ hat. |
<br> | <br> | ||
| − | e) Skizzieren Sie den Graphen von h(t) im Intervall $[-2;8]$ | + | e) Skizzieren Sie den Graphen von $h(t)$ im Intervall $[-2;8]$. |
<br> | <br> | ||
| − | f) Erklären Sie, wie mithilfe der Nullstellen der Funktion h(t) jener Zeitpunkt bestimmt werden kann, bei dem der Ball seine maximale Höhe erreicht. | + | f) Erklären Sie, wie mithilfe der Nullstellen der Funktion $h(t)$ jener Zeitpunkt bestimmt werden kann, bei dem der Ball seine maximale Höhe erreicht. |
|2= | |2= | ||
| − | a) Es gilt $$h(t)=-0.1t^2+0.3t+3$$. Bereits | + | a) Es gilt $$h(t)=-0.1t^2+0.3t+3$$. Bereits an $c=3$ erkennt man, dass die Anfangshöhe 3$m$ ist. Alternativ kann man auch für $t=0$ einsetzen (da hier der Beginn ist): |
$$h(0)=-0.1\cdot 0^2+0.3\cdot 0+3$$ | $$h(0)=-0.1\cdot 0^2+0.3\cdot 0+3$$ | ||
$$h(0)=3$$ | $$h(0)=3$$ | ||
| Zeile 189: | Zeile 184: | ||
| − | c) Gesucht ist die Nullstelle der Funktion. D.h. für welches t gilt, dass $h(t)=0$ ist: | + | c) Gesucht ist die Nullstelle der Funktion. D. h. für welches $t$ gilt, dass $h(t)=0$ ist: |
$$0=h(t)$$ | $$0=h(t)$$ | ||
$$0=-0.1t^2+0.3t+3$$ | $$0=-0.1t^2+0.3t+3$$ | ||
| − | Nun löst man die Gleichung z.B. mit der [[Quadratische_Gleichungen#L.C3.B6sung_der_allgemeinen_Form_-_die_gro.C3.9Fe_L.C3.B6sungsformel| großen Lösungsformel]] oder mit dem [[GeoGebra|Löse-Befehl]] und erhält: | + | Nun löst man die Gleichung z. B. mit der [[Quadratische_Gleichungen#L.C3.B6sung_der_allgemeinen_Form_-_die_gro.C3.9Fe_L.C3.B6sungsformel| großen Lösungsformel]] oder mit dem [[GeoGebra|Löse-Befehl]] und erhält: |
$$t_1=-4.18\ \ \ \textrm{ und }\ \ \ t_2=7.18$$ | $$t_1=-4.18\ \ \ \textrm{ und }\ \ \ t_2=7.18$$ | ||
| − | Der Ball landet nach 7.18 s auf dem Boden. | + | Der Ball landet nach $7.18 s$ auf dem Boden. |
| − | d) Für welches t ist $h(t)=2$? | + | d) Für welches $t$ ist $h(t)=2$? |
$$2=h(t)$$ | $$2=h(t)$$ | ||
$$2=-0.1t^2+0.3t+3\ \ \ \vert -2$$ | $$2=-0.1t^2+0.3t+3\ \ \ \vert -2$$ | ||
$$0=-0.1t^2+0.3t+1$$ | $$0=-0.1t^2+0.3t+1$$ | ||
| − | Nun löst man die Gleichung z.B. mit der [[Quadratische_Gleichungen#L.C3.B6sung_der_allgemeinen_Form_-_die_gro.C3.9Fe_L.C3.B6sungsformel| großen Lösungsformel]] oder mit dem [[GeoGebra|Löse-Befehl]] und erhält: | + | Nun löst man die Gleichung z. B. mit der [[Quadratische_Gleichungen#L.C3.B6sung_der_allgemeinen_Form_-_die_gro.C3.9Fe_L.C3.B6sungsformel| großen Lösungsformel]] oder mit dem [[GeoGebra|Löse-Befehl]] und erhält: |
$$t_1=-2\ \ \ \textrm{ und }\ \ \ t_2=5$$ | $$t_1=-2\ \ \ \textrm{ und }\ \ \ t_2=5$$ | ||
| − | Somit hat der Ball nach 5 Sekunden eine Höhe von 2 m. | + | Somit hat der Ball nach $5$ Sekunden eine Höhe von $2 m$. |
e) | e) | ||
[[Datei:Quadratische-fkten-Bsp.png|700px|miniatur|zentriert|Graph der Funktion $h(t)$]] | [[Datei:Quadratische-fkten-Bsp.png|700px|miniatur|zentriert|Graph der Funktion $h(t)$]] | ||
| − | + | f) Nach c) lauten die Nullstellen $t_1=-4.18$ und $t_2=7.18$. Da die Parabel symmetrisch zum Scheitelpunkt ist und die Parabel nach unten offen ist ($a=-0.1<0$), liegt der Scheitelpunkt/Hochpunkt genau zwischen den beiden Nullstellen: | |
$t_{max}=\frac{-4.18+7.18}{2}=1.5$ | $t_{max}=\frac{-4.18+7.18}{2}=1.5$ | ||
| − | + | Nach $1.5 s$ erreicht der Ball seine maximale Höhe. | |
| − | Nach 1.5 s erreicht der Ball seine maximale Höhe. | + | |
| Zeile 239: | Zeile 233: | ||
[[Grün: Arbeitsblätter | <span style="background-color:#00CD00"> $Aha!$ </span>]] $\ $ In diesem [http://www.geogebratube.org/student/m137542 diesem Arbeitsblatt] kannst du die Bedeutung der Scheitelpunktform genauer lernen. | [[Grün: Arbeitsblätter | <span style="background-color:#00CD00"> $Aha!$ </span>]] $\ $ In diesem [http://www.geogebratube.org/student/m137542 diesem Arbeitsblatt] kannst du die Bedeutung der Scheitelpunktform genauer lernen. | ||
| − | [[Violett: Quizzes und dynamische Aufgabenblätter| <span style="background-color:#FF3E96"> ? </span>]] $\ $ Und hier findest du eine [http://www.geogebratube.org/student/m79503 Aufgabe zur Scheitelpunktform] | + | [[Violett: Quizzes und dynamische Aufgabenblätter| <span style="background-color:#FF3E96"> ? </span>]] $\ $ Und hier findest du eine [http://www.geogebratube.org/student/m79503 Aufgabe zur Scheitelpunktform]. |
<br> | <br> | ||
| Zeile 258: | Zeile 252: | ||
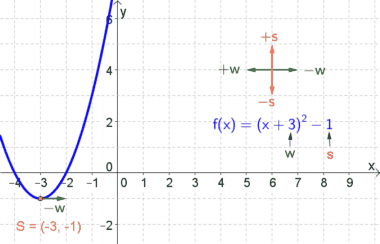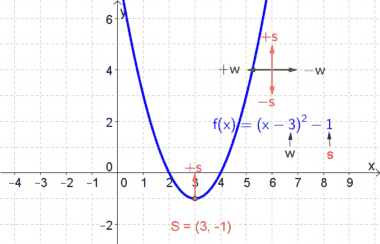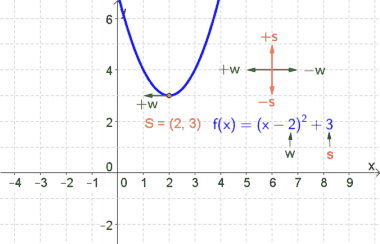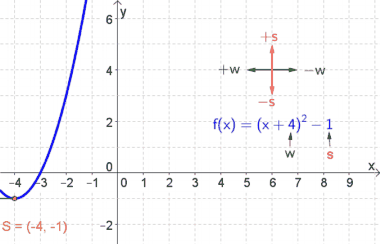
'''Lösung:''' | '''Lösung:''' | ||
| − | * $w=-2$... | + | * $w=-2$... Somit wird die Parabel um $2$ nach rechts verschoben. |
| − | * $s=1$... | + | * $s=1$... Somit wird die Parabel um $1$ hinauf verschoben. |
| − | * Der Scheitelpunkt S hat folglich die Koordinaten S(2|1). | + | * Der Scheitelpunkt $S$ hat folglich die Koordinaten $S(2|1)$. |
| − | * $a=0.5$... damit erhält man die Steigung, wenn man 1 nach rechts und 0.5 hinauf geht. | + | * $a=0.5$... damit erhält man die Steigung, wenn man $1$ nach rechts und $0.5$ hinauf geht. |
| Zeile 274: | Zeile 268: | ||
| − | === | + | === Vorteil der Scheitelpunktform === |
Die Scheitelpunktform hat den Vorteil, dass | Die Scheitelpunktform hat den Vorteil, dass | ||
| Zeile 280: | Zeile 274: | ||
a) bei gegebener Funktionsgleichung direkt die Koordinaten des Scheitelpunktes bestimmt werden können bzw. | a) bei gegebener Funktionsgleichung direkt die Koordinaten des Scheitelpunktes bestimmt werden können bzw. | ||
| − | b) bei gegebenem Graphen direkt mithilfe des Scheitelpunktes w uns s bestimmt werden können. | + | b) bei gegebenem Graphen direkt mithilfe des Scheitelpunktes $w$ uns $s$ bestimmt werden können. |
| Zeile 305: | Zeile 299: | ||
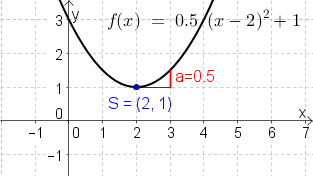
b) Wandeln Sie die Funktion in die Normalform $f(x)=ax^2+bx+c$ um. | b) Wandeln Sie die Funktion in die Normalform $f(x)=ax^2+bx+c$ um. | ||
| − | |2= a) $S(2\vert 1)$, da die Parabel 1 hinauf (=s...senkrecht) und 2 nach rechts (-2=w | + | |2= a) $S(2\vert 1)$, da die Parabel $1$ hinauf ($1=s$...senkrecht) und $2$ nach rechts ($-2=w$...waagrecht) verschoben wurde. |
b) Wir quadrieren die Klammer aus und vereinfachen (siehe [[Binomische Formeln]]: | b) Wir quadrieren die Klammer aus und vereinfachen (siehe [[Binomische Formeln]]: | ||
$$f(x)=0.5\cdot (x-2)^2+1$$ | $$f(x)=0.5\cdot (x-2)^2+1$$ | ||
| − | 1. Schritt: | + | 1. Schritt: Ausquadrieren |
$$f(x)=0.5\cdot (x^2-4x+4)+1$$ | $$f(x)=0.5\cdot (x^2-4x+4)+1$$ | ||
| − | 2. Schritt: | + | 2. Schritt: Vereinfachen |
$$f(x)=0.5x^2-2x+2+1$$ | $$f(x)=0.5x^2-2x+2+1$$ | ||
$$f(x)=0.5x^2-2x+3$$ | $$f(x)=0.5x^2-2x+3$$ | ||
| Zeile 329: | Zeile 323: | ||
$$f(x)=x^2-2\cdot 1\cdot x+(1+2)$$ | $$f(x)=x^2-2\cdot 1\cdot x+(1+2)$$ | ||
$$f(x)=(x^2-2\cdot 1\cdot x+1)+2$$ | $$f(x)=(x^2-2\cdot 1\cdot x+1)+2$$ | ||
| − | + | Nun die binomische Formel $a^2+2ab+b^2=(a+b)^2$ verwenden: | |
$$\underline{\underline{f(x)=(x-1)^2+2} }$$ | $$\underline{\underline{f(x)=(x-1)^2+2} }$$ | ||
Somit haben wir die Scheitelpunktform $f(x)=(x-1)^2+2$ und die Koordinaten des Scheitelpunktes lauten: $(1\vert 2)$ ($s=1$ und $w=+1\rightarrow$ 1 nach rechts) }} | Somit haben wir die Scheitelpunktform $f(x)=(x-1)^2+2$ und die Koordinaten des Scheitelpunktes lauten: $(1\vert 2)$ ($s=1$ und $w=+1\rightarrow$ 1 nach rechts) }} | ||
| Zeile 335: | Zeile 329: | ||
| − | |||
<br> | <br> | ||
<br> | <br> | ||
| − | '''Füge im folgenden Applet zu jeder Graphik die passende Funktion hinzu''' | + | '''Füge im folgenden Applet zu jeder Graphik die passende Funktion hinzu.''' |
{{#widget:Iframe | {{#widget:Iframe | ||
|url= http://LearningApps.org/view391866 | |url= http://LearningApps.org/view391866 | ||
| Zeile 351: | Zeile 344: | ||
| <div class="testbutton-blue"> {{#switchtablink:Funktionsgleichung bestimmen|$\rightarrow$ nächste Seite ...}} </div> | | <div class="testbutton-blue"> {{#switchtablink:Funktionsgleichung bestimmen|$\rightarrow$ nächste Seite ...}} </div> | ||
|} | |} | ||
| + | |||
= Funktionsgleichung bestimmen = | = Funktionsgleichung bestimmen = | ||
== Funktionsgleichung bestimmen == | == Funktionsgleichung bestimmen == | ||
| − | '''Typische Aufgabenstellung''' | + | '''Typische Aufgabenstellung:''' |
| − | : ''Bestimmen Sie die Funktionsgleichung der quadratischen Funktion, wenn mehrere Punkte auf der Parabel (=Graph der quadratischen Funktion) gegeben sind.'' | + | : ''Bestimmen Sie die Funktionsgleichung der quadratischen Funktion, wenn mehrere Punkte auf der Parabel ($=$ Graph der quadratischen Funktion) gegeben sind.'' |
'''Lösungsweg:''' Je nachdem, ob der Scheitelpunkt gegeben ist, gibt es zwei verschiedene Lösungswege: | '''Lösungsweg:''' Je nachdem, ob der Scheitelpunkt gegeben ist, gibt es zwei verschiedene Lösungswege: | ||
| − | a) Wenn der Scheitelpunkt gegeben ist, verwendet man die Scheitelpunktform und bestimmt anhand der Koordinaten des Scheitelpunktes $w$ und $s$ und anschließend $a$ | + | a) Wenn der Scheitelpunkt gegeben ist, verwendet man die Scheitelpunktform und bestimmt anhand der Koordinaten des Scheitelpunktes $w$ und $s$ und anschließend $a$. |
| − | b) Wenn der Scheitelpunkt nicht gegeben ist, verwendet man die Normalform und stellt mithilfe von 3 Punkten insgesamt 3 Gleichungen auf, indem man die Punkte in die Funktionsgleichung $y=a\cdot x^2+b\cdot x+c$ einsetzt. | + | b) Wenn der Scheitelpunkt nicht gegeben ist, verwendet man die Normalform und stellt mithilfe von $3$ Punkten insgesamt $3$ Gleichungen auf, indem man die Punkte in die Funktionsgleichung $y=a\cdot x^2+b\cdot x+c$ einsetzt. |
| − | + | ||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 373: | Zeile 366: | ||
|- | |- | ||
| '''Wird verwendet, wenn:''' | | '''Wird verwendet, wenn:''' | ||
| − | * Scheitelpunkt nicht bekannt ist | + | * Scheitelpunkt nicht bekannt ist |
| − | * 3 Punkte auf dem Graphen bekannt sind | + | * $3$ Punkte auf dem Graphen bekannt sind |
| − | * [[Nullstelle|Nullstellen]] berechnet werden müssen | + | * [[Nullstelle|Nullstellen]] berechnet werden müssen |
|'''Wird verwendet, wenn:''' | |'''Wird verwendet, wenn:''' | ||
| − | * Scheitelpunkt bekannt oder ablesbar ist | + | * Scheitelpunkt bekannt oder ablesbar ist |
|- | |- | ||
| '''Berechnung der [[Parameter]]''' | | '''Berechnung der [[Parameter]]''' | ||
| − | # Man bestimmt 3 Punkte des Graphen und setzt sie in die Funktionsgleichung. | + | # Man bestimmt $3$ Punkte des Graphen und setzt sie in die Funktionsgleichung ein. |
# Das daraus entstehende [[Gleichungssysteme (2.7.)#Gleichungssysteme mit 3 oder mehreren Variablen | Gleichungssystem]] wird gelöst. | # Das daraus entstehende [[Gleichungssysteme (2.7.)#Gleichungssysteme mit 3 oder mehreren Variablen | Gleichungssystem]] wird gelöst. | ||
| '''Berechnung der [[Parameter]]''' | | '''Berechnung der [[Parameter]]''' | ||
| − | # w und s können mithilfe des Scheitelpunktes $S=(w,s)$ bestimmt werden. | + | # $w$ und $s$ können mithilfe des Scheitelpunktes $S=(w,s)$ bestimmt werden. |
| − | # a erhält man | + | # $a$ erhält man, indem man einen weiteren Punkt aus dem Graphen in die Funktionsgleichung einsetzt oder $a$ aus dem Graphen abliest (''eins nach rechts, $a$ hinauf/hinab''). |
|- | |- | ||
|colspan="2" align="center" | '''Typische Aufgabenstellung:''' | |colspan="2" align="center" | '''Typische Aufgabenstellung:''' | ||
| − | Bestimmen Sie die Funktionsgleichung der abgebildeten Graphen | + | Bestimmen Sie die Funktionsgleichung der abgebildeten Graphen. |
|- | |- | ||
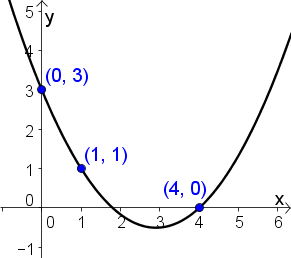
| | | | ||
| Zeile 416: | Zeile 409: | ||
Der Scheitelpunkt hat die Koordinaten $S(2|-1)$. Somit gilt: | Der Scheitelpunkt hat die Koordinaten $S(2|-1)$. Somit gilt: | ||
| − | $w=2$, da der Graph um 2 nach rechts verschoben wurde | + | $w=2$, da der Graph um $2$ nach rechts verschoben wurde. |
| − | $s=-1$, da der Graph um 1 hinunter verschoben wurde | + | $s=-1$, da der Graph um 1 hinunter verschoben wurde. |
$$\rightarrow y=a\cdot(x-2)^2-1$$ | $$\rightarrow y=a\cdot(x-2)^2-1$$ | ||
| − | Um $a$ zu berechnen, setzen wir nun den Punkt (0 | + | Um $a$ zu berechnen, setzen wir nun den Punkt $(0\vert 3)$ ein und erhalten: |
$$3=a\cdot (0-2)^2-1$$ | $$3=a\cdot (0-2)^2-1$$ | ||
$$3=a\cdot 4-1$$ | $$3=a\cdot 4-1$$ | ||
| Zeile 434: | Zeile 427: | ||
===Online-Übung zur Bestimmung der Funktionsgleichung=== | ===Online-Übung zur Bestimmung der Funktionsgleichung=== | ||
| − | Bestimme die Funktionsgleichung der Quadratischen Funktion mit $f(x)=ax^2+bx+c$ mithilfe der gegebenen Punkte | + | Bestimme die Funktionsgleichung der Quadratischen Funktion mit $f(x)=ax^2+bx+c$ mithilfe der gegebenen Punkte. <ggb_applet width="500" height="450e" version="5.0" id="Ye3p7Nst" /> |