Rentenrechnung: Unterschied zwischen den Versionen
(→Musterbeispiel für Berechnung des Restbetrages) |
K (Textersetzung - „http://snvbrwvobs2.snv.at/matura.wiki/“ durch „https://www1.vobs.at/maturawiki/“) |
||
| (25 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Definition: Rente== | == Definition: Rente== | ||
| − | {| | + | {{Vorlage:Definition|1=Unter einer '''Rente''' versteht man Einzahlungen, die |
| − | + | ||
| − | + | ||
*<p style="background-color:#E0E0E0"> in gleichen Zeitabständen </p> UND | *<p style="background-color:#E0E0E0"> in gleichen Zeitabständen </p> UND | ||
*<p style="background-color:#E0E0E0"> immer in gleicher Höhe </p> | *<p style="background-color:#E0E0E0"> immer in gleicher Höhe </p> | ||
getätigt werden. | getätigt werden. | ||
| − | Die Einzahlungen werden als '''Raten''' (R) bezeichnet. | + | Die Einzahlungen werden als '''Raten''' (R) bezeichnet.}} |
| − | + | ||
| − | + | Beispiele einer Rente sind: | |
* Taschengeld (jeden Monat erhälst du denselben Betrag von deinen Eltern) | * Taschengeld (jeden Monat erhälst du denselben Betrag von deinen Eltern) | ||
* Bausparer (jeden Monat oder jedes Jahr wird ein konstanter Betrag eingezahlt) | * Bausparer (jeden Monat oder jedes Jahr wird ein konstanter Betrag eingezahlt) | ||
| Zeile 117: | Zeile 114: | ||
</div> | </div> | ||
| + | In der Notation des offiziellen Formelheftes für die Matura lautet die Formeln folgendermaßen (wobei q=r ist): | ||
| + | {|align="center" border="2" | ||
| + | !| | ||
| + | !|vorschüssig | ||
| + | !|nachschüssig | ||
| + | |- align="center" | ||
| + | !| Endwert | ||
| + | |$$E=R\cdot q\cdot\frac{q^n-1}{q-1}$$ | ||
| + | |$$E=R\cdot \frac{q^n-1}{q-1}$$ | ||
| + | |- align="center" | ||
| + | !|Barwert | ||
| + | |$$B=R\cdot\frac{q^n-1}{q-1} \cdot \frac{1}{q^{n-1} }$$ | ||
| + | |$$B=R\cdot \frac{q^n-1}{q-1}\cdot \frac{1}{q^n }$$ | ||
| + | |} | ||
| − | == Musterbeispiel einer ganzjährigen Rente == | + | ==Musterbeispiel einer ganzjährigen Rente== |
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width: 800px;"> | ||
| − | < | + | <span style=""color: #A020F0;"> '''Angabe:''' Frau Aah zahlt 15 Jahre lang am Anfang jedes Jahres € 1000 auf ein mit 4% verzinstes Sparbuch ein.</span> |
| − | + | a) Bestimme den nach 15 Jahren angesparten Betrag. Beachte dabei die [[KESt]] von 25%. | |
| − | + | b) Von dem ersparten Geld will sie 20 vorschüssige Jahresraten beheben, die 5 Jahre nach der letzten Einzahlung beginnen. Berechnen Sie die Höhe der Rate. | |
| − | + | <div class="mw-collapsible-content"> | |
| − | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width: 800px;"> | ||
| + | <span style=""color: #A020F0;"> '''Lösung a)'''</span> | ||
| − | + | <div class="mw-collapsible-content"> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <div class="mw-collapsible-content"> | + | |
* $R=1000$ | * $R=1000$ | ||
| − | * $i_{eff}=4\cdot 0.75=3\% | + | * $i_{eff}=4\cdot 0.75=3\% \rightarrow r=1.03$ |
* $n=15$ | * $n=15$ | ||
* vorschüssig (da am Anfang vom Jahr eingezahlt wird) | * vorschüssig (da am Anfang vom Jahr eingezahlt wird) | ||
| Zeile 152: | Zeile 161: | ||
Somit hat Frau Aah nach 15 Jahren € 19156.88 angespart. | Somit hat Frau Aah nach 15 Jahren € 19156.88 angespart. | ||
| + | </div> | ||
</div> | </div> | ||
| − | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width: 800px;"> | ||
| − | < | + | <span style=""color: #A020F0;"> '''Lösung b)''' </span> |
| − | + | <div class="mw-collapsible-content"> | |
| − | + | ||
| − | <div class="mw-collapsible-content"> | + | |
Der Satz "''die 5 Jahre nach der letzten Einzahlung beginnen''" sagt uns, dass der Betrag $E_{15}$ fünf Jahre lang auf der Bank liegen bleibt. Durch Aufzinsen erhalten wir nun den Betrag nach diesen 5 Jahren (d.h. nach insgesamt 20 Jahren von Beginn weg): | Der Satz "''die 5 Jahre nach der letzten Einzahlung beginnen''" sagt uns, dass der Betrag $E_{15}$ fünf Jahre lang auf der Bank liegen bleibt. Durch Aufzinsen erhalten wir nun den Betrag nach diesen 5 Jahren (d.h. nach insgesamt 20 Jahren von Beginn weg): | ||
| Zeile 168: | Zeile 176: | ||
$$ E_{20}=22208.07$$ | $$ E_{20}=22208.07$$ | ||
| − | Nach 20 Jahren liegen somit € 22208.07 auf der Bank. Nun will Frau Aah von diesem Betrag 20 vorschüssige Jahresraten abheben. | + | Nach 20 Jahren liegen somit € 22208.07 auf der Bank. Nun will Frau Aah von diesem Betrag 20 vorschüssige Jahresraten abheben. |
| − | Das | + | Das angesparte Geld $E_{20}$ ist jener Wert ''am ANFANG'' der Auszahlungen. Somit ist $E_{20}=B$ der neue Barwert. |
| − | *$B=E_{20}=22208.07$ | + | * $B=E_{20}=22208.07$ |
| − | *$n=20$ | + | * $n=20$ |
| − | *$r=1.03 \rightarrow v=0.97087\dots $ | + | * $r=1.03 \rightarrow v=0.97087\dots $ |
| − | *$R=?$ | + | * $R=?$ |
| − | *vorschüssig | + | * vorschüssig |
Mit der Formel für den vorschüssigen Barwert erhalten wir: | Mit der Formel für den vorschüssigen Barwert erhalten wir: | ||
| Zeile 184: | Zeile 192: | ||
$$ \underline{\underline{1449.25=R}}$$ | $$ \underline{\underline{1449.25=R}}$$ | ||
| − | Antwort: Frau Aah kann 20 Jahre lang € 1449.25 abheben. | + | Antwort: Frau Aah kann 20 Jahre lang € 1449.25 abheben. |
| − | FN (N =20, I% = | + | FN (N =20, I% = 3, PV =Ergebnis von a) aufgezinst, PMT = solve, FV = 0, P/Y = 1, C/Y = 1, Beginn) |
| + | </div> | ||
</div> | </div> | ||
| − | |||
| + | </div> | ||
| + | </div> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ==Musterbeispiel einer unterjährigen Rente== | ||
| + | Wichtig!! Wenn die Raten mehrmals im Jahr eingezahlt werden, muss zuerst der passende [[Zins- und Zinseszinsrechnung#b) der konforme (äquivalente) Zinssatz |äquivalente Zinssatz]] berechnet werden. | ||
| − | + | z.B.: Wird monatlich eingezahlt, so brauchen wir den (äquivalenten) Monatszinssatz $i_{12}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | + | <div class="toccolours mw-collapsible mw-collapsed" style="width: 800px;"> |
| − | <span style="color:#A020F0> '''Angabe:''' Frau Des nimmt einen Kredit von € | + | <span style=""color: #A020F0;"> '''Angabe:''' Frau Des nimmt einen Kredit von € 15000,‐ mit einer Laufzeit von 10 Jahren auf, den sie in |
nachschüssigen Monatsraten zurückzahlen will (i = 5%). Berechnen Sie die Höhe der Raten. | nachschüssigen Monatsraten zurückzahlen will (i = 5%). Berechnen Sie die Höhe der Raten. | ||
| − | <br> </span> | + | <br /> </span> |
| − | <div class="mw-collapsible-content"> | + | <div class="mw-collapsible-content"> |
'''Lösung''' | '''Lösung''' | ||
| − | *$B=15000$ | + | * $B=15000$ |
| − | *$n=10\cdot 12=120$ | + | * $n=10\cdot 12=120$ |
| − | *$i=5\% \rightarrow r_1=1.05 \rightarrow r_{12}=\sqrt[12]{1.05} | + | * $i=5\% \rightarrow r_1=1.05 \rightarrow r_{12}=\sqrt[12]{1.05} \rightarrow r_{12}=1.00407\dots \rightarrow v_{12}=0.99594\dots$ |
| − | *nachschüssig | + | * nachschüssig |
| − | *$R=$? | + | * $R=$? |
| − | Durch Verwendung der [[Rentenrechnung#Formeln |nachschüssigen | + | Durch Verwendung der [[Rentenrechnung#Formeln |nachschüssigen Barwertformel]] ergibt sich: |
$\begin{align} | $\begin{align} | ||
| − | B&=R\cdot v\cdot \frac{v^{120}-1}{v-1} & | + | B&=R\cdot v\cdot \frac{v^{120}-1}{v-1} & & |\cdot (v-1) && \textrm{und} : (v\cdot (v^{120}-1))\\ |
\end{align}$ | \end{align}$ | ||
$\begin{align} | $\begin{align} | ||
| − | \frac{B\cdot (v-1)}{v\cdot(v^{120}-1)}&=R &&\\ | + | \frac{B\cdot (v-1)}{v\cdot(v^{120}-1)}&&=R &&\\ |
\end{align}$ | \end{align}$ | ||
$$ \underline{\underline{158.29=R}} $$ | $$ \underline{\underline{158.29=R}} $$ | ||
| − | Antwort: Sie muss | + | Antwort: Sie muss monatlich € 158.29 einzahlen. |
| − | FN (N = 120, I% =100(1,05^(1/12)‐1), PV = | + | FN (N = 120, I% =100(1,05^(1/12)‐1), PV = -15000, PMT = solve, FV =0, P/Y = 1, C/Y= 1, END)$\rightarrow$ PMT=158.29 |
| + | <br /> | ||
Achtung: P/Y bezeichnet die Einzahlungen pro Zinsperiode. Diese ist nun aber 1! | Achtung: P/Y bezeichnet die Einzahlungen pro Zinsperiode. Diese ist nun aber 1! | ||
| − | (Alternative: FN (N = 120, I% =5, PV = | + | <br /> |
| + | (Alternative: FN (N = 120, I% =5, PV = -15000, PMT = solve, FV =0, P/Y = 12, C/Y= 1, END)$\rightarrow$ PMT= 158.29) | ||
</div> | </div> | ||
| − | |||
</div> | </div> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| − | + | == Musterbeispiel für eine Rentenrechnung mit Restbetrag == | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | == Musterbeispiel für eine Rentenrechnung mit | + | |
<div class="toccolours mw-collapsible mw-collapsed" style="width:900px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:900px"> | ||
<span style="color:#A020F0> | <span style="color:#A020F0> | ||
| − | Auf Petras Sparbuch befindet sich momentan ein | + | Auf Petras Sparbuch befindet sich momentan ein hoher Geldbetrag, von dem sie die nächsten 16 Jahre lang jährlich nachschüssig je € 1000 abheben könnte. (i=5 % p.a.) |
| − | * Berechne, wie oft sie dafür statt € | + | * Berechne, wie oft sie dafür statt € 1000 insgesamt € 2000 jedes Halbjahr abheben könnte. |
* Ermittle zusätzlich, wie hoch der Restbetrag ist, der zeitgleich mit der letzten Vollrate fällig ist. | * Ermittle zusätzlich, wie hoch der Restbetrag ist, der zeitgleich mit der letzten Vollrate fällig ist. | ||
</span> | </span> | ||
| Zeile 263: | Zeile 271: | ||
!| Berechnung mit dem [[Rentenrechnung#TVM-Solver (Rechnen im TR) | TVM-Solver]] | !| Berechnung mit dem [[Rentenrechnung#TVM-Solver (Rechnen im TR) | TVM-Solver]] | ||
|- | |- | ||
| − | !colspan="2" | 1. Zuerst berechnen wir den Barwert von Petras 16 nachschüssigen Abhebungen (= wie viel hat sie heute auf dem Konto, um 16 | + | !colspan="2" | 1. Zuerst berechnen wir den Barwert von Petras 16 nachschüssigen Abhebungen (= wie viel hat sie heute auf dem Konto, um 16 Mal € 1000 abzuheben) |
|- | |- | ||
| | | | ||
| Zeile 317: | Zeile 325: | ||
|- | |- | ||
| − | ! colspan="2" |3. Zuletzt berechnen wir den Restbetrag, jenen Betrag, der bei der letzten Abhebung von € 2000 noch auf dem Konto bleibt. Die folgende Graphik soll den Sachverhalt verdeutlichen | + | ! colspan="2" |3. Zuletzt berechnen wir den Restbetrag, jenen Betrag, der bei der letzten Abhebung von € 2000 noch auf dem Konto bleibt. Die folgende Graphik soll den Sachverhalt verdeutlichen. |
[[Datei:Bsp mit Restbetrag.png|thumb|1200px|center|Darstellung aller Auszahlungen (rot)]] | [[Datei:Bsp mit Restbetrag.png|thumb|1200px|center|Darstellung aller Auszahlungen (rot)]] | ||
| Zeile 328: | Zeile 336: | ||
|Sei B_5 der Barwert der 5 Auszahlungen von € 2000, dann kann die obige Abbildung mithilfe des [[Äquivalenzprinzip (Vergleich von Einzahlungen) | Äquivalenzprinzips]] folgendermaßen angeschrieben werden: | |Sei B_5 der Barwert der 5 Auszahlungen von € 2000, dann kann die obige Abbildung mithilfe des [[Äquivalenzprinzip (Vergleich von Einzahlungen) | Äquivalenzprinzips]] folgendermaßen angeschrieben werden: | ||
$$ 10837.77 = B_5 +\frac{ \textrm{Restbetrag}}{(r_2)^5}$$ | $$ 10837.77 = B_5 +\frac{ \textrm{Restbetrag}}{(r_2)^5}$$ | ||
| − | Zusätzlich erhält man $B_5$ mithilfe der nachschüssigen Barwertformel $ B_5=R\cdot v_2 \cdot \frac{(v_2)^5-1}{v_2-1} $, wobei $R= | + | Zusätzlich erhält man $B_5$ mithilfe der nachschüssigen Barwertformel $ B_5=R\cdot v_2 \cdot \frac{(v_2)^5-1}{v_2-1} $, wobei $R=2000$ und $v_2=0.975…$ (siehe oben) ist. Dadurch erhält man: |
$$ B_5=9299.82$$ | $$ B_5=9299.82$$ | ||
| − | Der Barwert aller Abhebungen in den 5 Semestern beträgt 9299.82 | + | Der Barwert aller Abhebungen in den 5 Semestern beträgt 9299.82. |
Daraus ergibt sich für den Restbetrag, dass | Daraus ergibt sich für den Restbetrag, dass | ||
$$ B=B_5+\frac{Restbetrag}{(r_2)^5} $$ | $$ B=B_5+\frac{Restbetrag}{(r_2)^5} $$ | ||
| Zeile 345: | Zeile 353: | ||
| | | | ||
| − | Wir wollen also wissen, wie viel am Ende (=FV=Restbetrag) noch auf dem Konto bleibt, wenn wir | + | Wir wollen also wissen, wie viel am Ende (=FV=Restbetrag) noch auf dem Konto bleibt, wenn wir 5 Mal (N=5) abgehoben haben: |
*N=5 | *N=5 | ||
| Zeile 360: | Zeile 368: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
<br> | <br> | ||
| + | <br> | ||
| + | |||
| + | == Musterbeispiel mit Anzahlung + Rente + Restwert (Leasing) == | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| + | |||
| + | <span style="color:#A020F0> | ||
| + | |||
| + | Anna plant ein Fahrzeug im Wert von € 21000 zu leasen. Der Händler macht ihr dabei das folgende Angebot: Sie muss € 5000 als Anzahlung sofort überweisen und die nächsten 36 Monate nachschüssig eine bestimmte Monatsrate einzahlen. Nach den 36 Monaten beträgt der Restwert noch € 9000. Bestimmen Sie die Höhe der Rate, wenn mit einem Zinssatz von 3 % p.a. gerechnet wird. | ||
| + | |||
| + | </span> | ||
| + | |||
| + | <div class="mw-collapsible-content"> | ||
| + | |||
| + | '''Lösung:''' | ||
| + | {| border="1" | ||
| + | |||
| + | |- | ||
| + | !| Händische Berechnung | ||
| + | !| Berechnung mit dem [[Rentenrechnung#TVM-Solver (Rechnen im TR) | TVM-Solver]] | ||
| + | |- | ||
| + | !colspan="2" | Zuerst veranschaulichen wir die Zahlungen graphisch: | ||
| + | |||
| + | [[Datei:Leasing-Bsp.png|thumb|400px|center|Darstellung der Aus- (rot) und Einzahlungen (grün)]] | ||
| + | |||
| + | |||
| + | |- | ||
| + | | Beim händischen Rechnen werden alle Zahlungen auf einen Zeitpunkt verzinst (siehe [[Äquivalenzprinzip | Äquivalenzprinzip (Vergleich von Einzahlungen)]]. Hier wird nun alles auf das dritte Jahr (=36 Monate) aufgezinst (genauso gut könnte aber auch alles auf den Beginn abgezinst werden). | ||
| + | |||
| + | Aus der der Graphik ergibt sich damit die folgende Gleichung: | ||
| + | |||
| + | $$21000\cdot r^3=5000 \cdot r^3+ \textrm{Endwert der 36 nachschüssigen Monatsraten} + 9000 $$ | ||
| + | $$ 21000\cdot 1.03^3=5000 \cdot 1.03^3+ R\cdot\frac{r_{12}^{36}-1}{r_{12}-1} + 9000 $$ | ||
| + | wobei $r_{12}=\sqrt[12]{1.03}=1.002466$ der monatliche Aufzinsungsfaktor ist. | ||
| + | |||
| + | Mithilfe des [[Solve-Befehl | Solve-Befehls]] erhält man: | ||
| + | $$\underline{\underline{R=225.64}}$$ | ||
| + | |||
| + | A: Die monatliche Rate liegt bei € 225.64. | ||
| + | |||
| + | |||
| + | |||
| + | | | ||
| + | TVM-Solver: | ||
| + | *N=36, | ||
| + | *i=3, | ||
| + | *PV=-21000 + 5000 (da 21000 Schulden und 5000 sofort eingezahlt werden) | ||
| + | *PMT=? $\rightarrow \underline{\underline{PMT=225.64}}$ | ||
| + | *FV=9000 (da € 9000 der Restwert ist), | ||
| + | *P/Y=12, | ||
| + | *C/Y=1, | ||
| + | *End | ||
| + | |} | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 372: | Zeile 437: | ||
Im Ti 82 kannst du die Beispiele auch im Taschenrechner mit dem TVM-Solver lösen. | Im Ti 82 kannst du die Beispiele auch im Taschenrechner mit dem TVM-Solver lösen. | ||
| − | Hier findest du eine [ | + | Hier findest du eine [https://www1.vobs.at/maturawiki/index.php?action=ajax&title=-&rs=SecureFileStore::getFile&f=/3/33/TVM-Solver.pdf Erklärung des Programms] |
<br> | <br> | ||
<br> | <br> | ||
| + | |||
| + | == Finanzmathematik-Befehle für GeoGebra == | ||
| + | [[Media:GeoGebra-Befehle für die Finanzmathematik.docx | Word-Dokument mit den wichtigsten GeoGebra-Befehlen für die Finanzmathematik]] | ||
== Beispiele == | == Beispiele == | ||
| − | [http://aufgabenpool. | + | * [[Bifie-grün: Aufgaben des Bifie | <span style="background-color:#7CFC00">$Bifie$</span>]] [http://aufgabenpool.srdp.at/bhs/download.php?qid=47&file=Sparkonto.pdf Sparkonto (Bifie-Aufgabe)] |
| + | |||
| + | * [[Bifie-grün: Aufgaben des Bifie | <span style="background-color:#7CFC00">$Bifie$</span>]] [http://aufgabenpool.srdp.at/bhs/download.php?qid=49&file=Kreditkonditionen.pdf Kreditkonditionen (Bifie-Aufgabe)] | ||
| + | |||
| + | * [[Bifie-grün: Aufgaben des Bifie | <span style="background-color:#7CFC00">$Bifie$</span>]] [http://aufgabenpool.srdp.at/bhs/download.php?qid=54&file=Bausparen_bis_2011.pdf Bausparen (Bifie-Aufgabe)] | ||
| + | |||
| + | * [[Bifie-grün: Aufgaben des Bifie | <span style="background-color:#7CFC00">$Bifie$</span>]] [http://aufgabenpool.srdp.at/bhs/download.php?qid=91&file=Immobilienhandel.pdf Immobilienhandel (Bifie-Aufgabe mit Schuldentilgung)] | ||
| + | Siehe auch [[Schuldentilgung]] | ||
| + | |||
| + | * [[Bifie-grün: Aufgaben des Bifie | <span style="background-color:#7CFC00">$Bifie$</span>]] [http://aufgabenpool.srdp.at/bhs/download.php?qid=92&file=Ruecklage.pdf Rücklage (Bifie-Aufgabe)] | ||
| + | |||
| + | {{Vorlage:Bifie-Aufgabe|1=https://aufgabenpool.srdp.at/bhs/download.php?qid=429&file=Autokauf_(2).pdf Autokauf_(2)}} | ||
| + | |||
| + | {{Vorlage:Bifie-Aufgabe|1=https://aufgabenpool.srdp.at/bhs/download.php?qid=456&file=Stallbaufinanzierung.pdf Stallbaufinanzierung}} | ||
| + | |||
| + | {{Vorlage:Bifie-Aufgabe|1=https://aufgabenpool.srdp.at/bhs/download.php?qid=486&file=Sparbuch.pdf Sparbuch}} | ||
| + | |||
| + | {{Vorlage:Bifie-Aufgabe|1=https://aufgabenpool.srdp.at/bhs/download.php?qid=462&file=Produzent_von_landwirtschaftlichen_Geraeten.pdf Produzent von landwirtschaftlichen Geräten}} | ||
| + | :Siehe auch: [[Kosten- und Preistheorie]] sowie [[Binomialverteilung]] | ||
| + | |||
| + | {{Vorlage:Bifie-Aufgabe|1=https://aufgabenpool.srdp.at/bhs/download.php?qid=483&file=Geraetekauf.pdf Gerätekauf}} | ||
| + | |||
| + | {{Vorlage:Bifie-Aufgabe|1=https://aufgabenpool.srdp.at/bhs/download.php?qid=406&file=Lebensversicherung.pdf Lebensversicherung}} | ||
| + | : Siehe auch: [[Wachstums- und Zerfallsprozesse]] sowie [[Wahrscheinlichkeit: Baumdiagramme und Pfadregeln]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Kategorie:Finanzmathematik]] | [[Kategorie:Finanzmathematik]] | ||
Aktuelle Version vom 29. Mai 2019, 10:46 Uhr
Inhaltsverzeichnis
- 1 Definition: Rente
- 2 Begriffe
- 3 Musterbeispiel
- 4 Formeln
- 5 Musterbeispiel einer ganzjährigen Rente
- 6 Musterbeispiel einer unterjährigen Rente
- 7 Musterbeispiel für eine Rentenrechnung mit Restbetrag
- 8 Musterbeispiel mit Anzahlung + Rente + Restwert (Leasing)
- 9 TVM-Solver (Rechnen im TR)
- 10 Finanzmathematik-Befehle für GeoGebra
- 11 Beispiele
Definition: Rente
|
Unter einer Rente versteht man Einzahlungen, die
getätigt werden. Die Einzahlungen werden als Raten (R) bezeichnet. |
Beispiele einer Rente sind:
- Taschengeld (jeden Monat erhälst du denselben Betrag von deinen Eltern)
- Bausparer (jeden Monat oder jedes Jahr wird ein konstanter Betrag eingezahlt)
- "Rente" in der Pension (der Pensionist erhält monatlich einen fixen Betrag überwiesen)
Begriffe
Neben der Rate R (=Betrag, der regelmäßig eingezahlt wird) unterscheidet man folgende Punkte:
| Unterscheidungsmerkmal | Anfang | Ende |
|---|---|---|
Zeitpunkt der Einzahlung |
vorschüssig
= am Anfang der Zahlungsperiode |
nachschüssig
= am Ende der Zahlungsperiode |
Zeitpunkt des Gesamtwertes |
Barwert
= Gesamtwert am Anfang der Rentenzahlungen (z.B.: welche Schuld muss abgezahlt werden) |
Endwert
= Gesamtwert am Ende der Rentenzahlungen (Welcher Betrag wurde angespart) |
Einzahlungsperiode |
Ganzjährige Rente
=Einzahlungen erfolgen jährlich |
Unterjährige Rente
= Einzahlungen erfolgen mehrmals im Jahr (z.B. monatlich). |
!Wichtig! Bei unterjährigen Renten muss der äquivalente Zinssatz berechnet werden.
Musterbeispiel
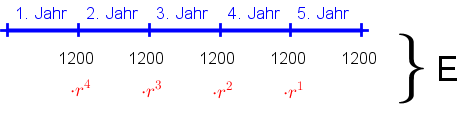
Anna schließt für sich einen Bausparvertrag mit 4% Verzinsung ab, bei dem sie am Ende jeden Jahres 1200 € einzahlt. Wie hoch ist der angesparte Betrag nach 5 Jahren (ohne staatliche Prämie)? Rechne mit einer KESt von 25%.
Lösung
- Gegeben und Gesucht
- Rate R=1200
- nachschüssig (Zahlungen am Ende des Jahres)
- ganzjährige Rente (Zahlungen einmal jährlich)
- $i=4\%$
$\begin{align} \rightarrow& i_{eff}=4\cdot 0.75 = 3\%\\ \rightarrow& r=1+\frac{i_{eff}}{100}=1.03 \end{align} $ - Endwert E=? (Anna will wissen, wie viel sie am Ende angespart hat)
- Berechnung $$ 1200\cdot 1.03^4 + 1200\cdot 1.03^3 + 1200\cdot 1.03^2 + 1200\cdot 1.03 + 1200 = E $$ $$ \underline{\underline{6370.96=E}} $$
- Antwortsatz
- Nach 5 Jahren hat Anna einen Betrag von € 6370.96 angespart.
Formeln
Sei
- $ n\dots$ die Anzahl der Einzahlungen
- $ r\dots $ der (äuqivalente) Aufzinsungsfaktor
- $ v\dots $ der (äquivalente) Abzinsungsfaktor $v=\frac{1}{r}$
| vorschüssig | nachschüssig | |
|---|---|---|
| Endwert | $$E=R\cdot r\cdot\frac{r^n-1}{r-1}$$ | $$E=R\cdot \frac{r^n-1}{r-1}$$ |
| Barwert | $$B=R\cdot \frac{v^n-1}{v-1}$$ | $$B=R\cdot v\cdot \frac{v^n-1}{v-1}$$
|
Herleitung der Formeln
Hier siehst du die Herleitung der Formel für den nachschüssigen Endwert.$$E=R\cdot \frac{1-r^n}{1-r} $$ Die Herleitungen für die restlichen Formeln funktionieren ähnlich. Der Endwert setzt sich aus der Summe aller Einzahlungen zusammen. Nehmen wir an, wir berechnen den Endwert einer nachschüssigen Rente über n Jahre, dann erhält man den Endwert, indem man alle Einzahlung auf das Ende verzinst und dann zusammenaddiert:
$$ E= R + R\cdot r+ R\cdot r^2 + R\cdot r^3+\dots + R\cdot r^{n-1} $$ wobei $R\cdot r^{n-1}$ die erste Zahlung ist, die $n-1$ Jahre aufgezinst werden muss und $R$ die letzte Zahlung ist.
Dies ist nun eine sogenannte geometrische Reihe, da jeder Summand sich nur durch die Multiplikation mit r unterscheidet. Unter folgendem Link findest du die Herleitung der für die geometrische Formel $s_n=a_0\cdot \frac{1-q^n}{1-q} $, wobei $E=s_n$, $R=a_0$ und $r=q$ ist: Herleitung der Endwertformel
In der Notation des offiziellen Formelheftes für die Matura lautet die Formeln folgendermaßen (wobei q=r ist):
| vorschüssig | nachschüssig | |
|---|---|---|
| Endwert | $$E=R\cdot q\cdot\frac{q^n-1}{q-1}$$ | $$E=R\cdot \frac{q^n-1}{q-1}$$ |
| Barwert | $$B=R\cdot\frac{q^n-1}{q-1} \cdot \frac{1}{q^{n-1} }$$ | $$B=R\cdot \frac{q^n-1}{q-1}\cdot \frac{1}{q^n }$$
|
Musterbeispiel einer ganzjährigen Rente
Angabe: Frau Aah zahlt 15 Jahre lang am Anfang jedes Jahres € 1000 auf ein mit 4% verzinstes Sparbuch ein.
a) Bestimme den nach 15 Jahren angesparten Betrag. Beachte dabei die KESt von 25%.
b) Von dem ersparten Geld will sie 20 vorschüssige Jahresraten beheben, die 5 Jahre nach der letzten Einzahlung beginnen. Berechnen Sie die Höhe der Rate.
Lösung a)
- $R=1000$
- $i_{eff}=4\cdot 0.75=3\% \rightarrow r=1.03$
- $n=15$
- vorschüssig (da am Anfang vom Jahr eingezahlt wird)
- $E_{15} = $?
Mithilfe der vorschüssigen Endwertformel erhalten wir: $$ E_{15}=R\cdot r\cdot \frac{r^n-1}{r-1} $$ $$ E_{15}=1000 \cdot 1.03 \frac{1.03^{15}-1}{1.03-1} $$ $$\underline{\underline{E_{15}=19156.88}} $$
Somit hat Frau Aah nach 15 Jahren € 19156.88 angespart.
Lösung b)
Der Satz "die 5 Jahre nach der letzten Einzahlung beginnen" sagt uns, dass der Betrag $E_{15}$ fünf Jahre lang auf der Bank liegen bleibt. Durch Aufzinsen erhalten wir nun den Betrag nach diesen 5 Jahren (d.h. nach insgesamt 20 Jahren von Beginn weg): $$ E_{20}=E_{15}\cdot r^5$$ $$ E_{20}=19156.88\cdot 1.03^5$$ $$ E_{20}=22208.07$$
Nach 20 Jahren liegen somit € 22208.07 auf der Bank. Nun will Frau Aah von diesem Betrag 20 vorschüssige Jahresraten abheben. Das angesparte Geld $E_{20}$ ist jener Wert am ANFANG der Auszahlungen. Somit ist $E_{20}=B$ der neue Barwert.
- $B=E_{20}=22208.07$
- $n=20$
- $r=1.03 \rightarrow v=0.97087\dots $
- $R=?$
- vorschüssig
Mit der Formel für den vorschüssigen Barwert erhalten wir: $$ B=R\cdot \frac{v^{20}-1}{v-1} $$ $$ B\cdot (v-1)=R\cdot (v^{20}-1) $$ $$ \frac{B\cdot (v-1)}{(v^{20}-1)}=R $$ $$ \frac{22208.07\cdot (0.97087-1)}{(0.97087^{20}-1)}=R $$ $$ \underline{\underline{1449.25=R}}$$
Antwort: Frau Aah kann 20 Jahre lang € 1449.25 abheben.
FN (N =20, I% = 3, PV =Ergebnis von a) aufgezinst, PMT = solve, FV = 0, P/Y = 1, C/Y = 1, Beginn)
Musterbeispiel einer unterjährigen Rente
Wichtig!! Wenn die Raten mehrmals im Jahr eingezahlt werden, muss zuerst der passende äquivalente Zinssatz berechnet werden.
z.B.: Wird monatlich eingezahlt, so brauchen wir den (äquivalenten) Monatszinssatz $i_{12}$.
Angabe: Frau Des nimmt einen Kredit von € 15000,‐ mit einer Laufzeit von 10 Jahren auf, den sie in
nachschüssigen Monatsraten zurückzahlen will (i = 5%). Berechnen Sie die Höhe der Raten.
Lösung
- $B=15000$
- $n=10\cdot 12=120$
- $i=5\% \rightarrow r_1=1.05 \rightarrow r_{12}=\sqrt[12]{1.05} \rightarrow r_{12}=1.00407\dots \rightarrow v_{12}=0.99594\dots$
- nachschüssig
- $R=$?
Durch Verwendung der nachschüssigen Barwertformel ergibt sich:
$\begin{align} B&=R\cdot v\cdot \frac{v^{120}-1}{v-1} & & |\cdot (v-1) && \textrm{und} : (v\cdot (v^{120}-1))\\ \end{align}$
$\begin{align} \frac{B\cdot (v-1)}{v\cdot(v^{120}-1)}&&=R &&\\ \end{align}$
$$ \underline{\underline{158.29=R}} $$
Antwort: Sie muss monatlich € 158.29 einzahlen.
FN (N = 120, I% =100(1,05^(1/12)‐1), PV = -15000, PMT = solve, FV =0, P/Y = 1, C/Y= 1, END)$\rightarrow$ PMT=158.29
Achtung: P/Y bezeichnet die Einzahlungen pro Zinsperiode. Diese ist nun aber 1!
(Alternative: FN (N = 120, I% =5, PV = -15000, PMT = solve, FV =0, P/Y = 12, C/Y= 1, END)$\rightarrow$ PMT= 158.29)
Musterbeispiel für eine Rentenrechnung mit Restbetrag
Auf Petras Sparbuch befindet sich momentan ein hoher Geldbetrag, von dem sie die nächsten 16 Jahre lang jährlich nachschüssig je € 1000 abheben könnte. (i=5 % p.a.)
- Berechne, wie oft sie dafür statt € 1000 insgesamt € 2000 jedes Halbjahr abheben könnte.
- Ermittle zusätzlich, wie hoch der Restbetrag ist, der zeitgleich mit der letzten Vollrate fällig ist.
| Händische Berechnung | Berechnung mit dem TVM-Solver |
|---|---|
| 1. Zuerst berechnen wir den Barwert von Petras 16 nachschüssigen Abhebungen (= wie viel hat sie heute auf dem Konto, um 16 Mal € 1000 abzuheben) | |
$$ B=R\cdot v\cdot \frac{v^{16}-1}{v-1} $$ $$\underline{\underline{B=10.837.77}}$$ |
TVM-Solver:
|
| 2. Nun berechnen wir, wie oft Petra von den 10837.77 die € 2000 jedes halbe Jahr abheben kann. Gefragt ist also das n.
| |
|
!Achtung! Wenn mehrmals im Jahr abgehoben wird (=unterjährige Rente), brauchen wir beim händischen Rechnen den konformen Aufzinsungsfaktor $r_m$ In diesem Fall brauchen wir r_2, da jedes halbe Jahr abgehoben wird.
$$B=R\cdot v_2\cdot \frac{(v_2)^n-1}{v_2-1} \ \ \rightarrow n=5.89$$ Somit kann sie 5 Vollraten abheben, für die 6. Rate reicht es gerade nicht mehr aus (dies sind die 0.89)
|
Beim TVM-Sover brauchen wir den konformen Zinssatz nicht. Hier reicht es, für P/Y (=Zahlungen pro Jahr, Payments per Year) den Wert 2 einzusetzen:
|
| 3. Zuletzt berechnen wir den Restbetrag, jenen Betrag, der bei der letzten Abhebung von € 2000 noch auf dem Konto bleibt. Die folgende Graphik soll den Sachverhalt verdeutlichen.
| |
| Sei B_5 der Barwert der 5 Auszahlungen von € 2000, dann kann die obige Abbildung mithilfe des Äquivalenzprinzips folgendermaßen angeschrieben werden:
$$ 10837.77 = B_5 +\frac{ \textrm{Restbetrag}}{(r_2)^5}$$ Zusätzlich erhält man $B_5$ mithilfe der nachschüssigen Barwertformel $ B_5=R\cdot v_2 \cdot \frac{(v_2)^5-1}{v_2-1} $, wobei $R=2000$ und $v_2=0.975…$ (siehe oben) ist. Dadurch erhält man: $$ B_5=9299.82$$ Der Barwert aller Abhebungen in den 5 Semestern beträgt 9299.82. Daraus ergibt sich für den Restbetrag, dass $$ B=B_5+\frac{Restbetrag}{(r_2)^5} $$ $$ 10837.77= 9299.82+\frac{Restbetrag}{(r_2)^5} $$ $$ \frac{Restbetrag}{(r_2)^5} =1537.95 $$ $$\underline{\underline{Restbetrag=1737.46}}$$ Somit wird am Ende ein Restbetrag von zusätzlich € 1737.46 abgehoben. Alternativ hätte auch alles auf das Ende des 5. Semesters aufgezinst werden können. Hier hätten wir ebenfalls 1737.46 erhalten.
|
Wir wollen also wissen, wie viel am Ende (=FV=Restbetrag) noch auf dem Konto bleibt, wenn wir 5 Mal (N=5) abgehoben haben:
PMT= -2000
Somit beträgt der Restbetrag noch € 1737.46, die mit der letzten Rate ebenfalls abgehoben werden. |
Musterbeispiel mit Anzahlung + Rente + Restwert (Leasing)
Anna plant ein Fahrzeug im Wert von € 21000 zu leasen. Der Händler macht ihr dabei das folgende Angebot: Sie muss € 5000 als Anzahlung sofort überweisen und die nächsten 36 Monate nachschüssig eine bestimmte Monatsrate einzahlen. Nach den 36 Monaten beträgt der Restwert noch € 9000. Bestimmen Sie die Höhe der Rate, wenn mit einem Zinssatz von 3 % p.a. gerechnet wird.
Lösung:
| Händische Berechnung | Berechnung mit dem TVM-Solver |
|---|---|
| Zuerst veranschaulichen wir die Zahlungen graphisch:
| |
| Beim händischen Rechnen werden alle Zahlungen auf einen Zeitpunkt verzinst (siehe Äquivalenzprinzip (Vergleich von Einzahlungen). Hier wird nun alles auf das dritte Jahr (=36 Monate) aufgezinst (genauso gut könnte aber auch alles auf den Beginn abgezinst werden).
Aus der der Graphik ergibt sich damit die folgende Gleichung: $$21000\cdot r^3=5000 \cdot r^3+ \textrm{Endwert der 36 nachschüssigen Monatsraten} + 9000 $$ $$ 21000\cdot 1.03^3=5000 \cdot 1.03^3+ R\cdot\frac{r_{12}^{36}-1}{r_{12}-1} + 9000 $$ wobei $r_{12}=\sqrt[12]{1.03}=1.002466$ der monatliche Aufzinsungsfaktor ist. Mithilfe des Solve-Befehls erhält man: $$\underline{\underline{R=225.64}}$$ A: Die monatliche Rate liegt bei € 225.64.
|
TVM-Solver:
|
TVM-Solver (Rechnen im TR)
Im Ti 82 kannst du die Beispiele auch im Taschenrechner mit dem TVM-Solver lösen.
Hier findest du eine Erklärung des Programms
Finanzmathematik-Befehle für GeoGebra
Word-Dokument mit den wichtigsten GeoGebra-Befehlen für die Finanzmathematik
Beispiele
Siehe auch Schuldentilgung
$Bifie$ Produzent von landwirtschaftlichen Geräten
- Siehe auch: Kosten- und Preistheorie sowie Binomialverteilung