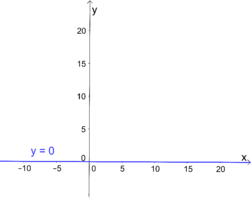Lineare Ungleichungen mit 2 Variablen: Unterschied zwischen den Versionen
Aus Matura Wiki
(→Ungleichungssysteme) |
|||
| (48 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
= Einleitung = | = Einleitung = | ||
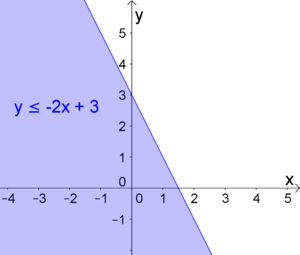
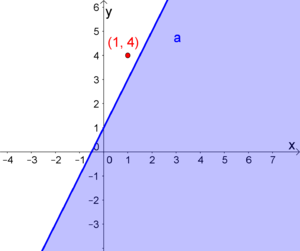
| − | [[Datei:Ungl-Intro.png|thumb|right|300px|Die Lösungsmenge einer linearen Ungleichung mit 2 Variablen ist eine Halbebene.]] | + | [[Datei:Ungl-Intro.png|thumb|right|300px|Die Lösungsmenge einer linearen Ungleichung mit $2$ Variablen ist eine Halbebene.]] |
| − | Lineare Ungleichungen | + | Lineare Ungleichungen setzen sich aus zwei [[Term|Termen]] zusammen, die durch eines der vier [[Ungleichung|Ungleichheitszeichen $\leq, <, \geq, >$]] verbunden sind. |
| − | Beispiele: $$y\leq 2x+3$$ | + | '''Beispiele:''' $$y\leq 2x+3$$ |
oder | oder | ||
$$2x-y>3$$ | $$2x-y>3$$ | ||
| Zeile 10: | Zeile 10: | ||
= Lösungsmenge einer linearen Ungleichung = | = Lösungsmenge einer linearen Ungleichung = | ||
== Lösungsmenge einer linearen Ungleichung == | == Lösungsmenge einer linearen Ungleichung == | ||
| − | Die Lösungsmenge einer linearen Ungleichung wird als sogenannte | + | Die Lösungsmenge einer linearen Ungleichung wird als sogenannte „Halbebene“ im Koordinatensystem eingezeichnet. |
| Zeile 17: | Zeile 17: | ||
<p style="color:#CAE1FF> | <p style="color:#CAE1FF> | ||
| − | Gib die Lösungsmenge der Ungleichung $2x-y\ | + | Gib die Lösungsmenge der Ungleichung $2x-y\geq -1$ graphisch in einem Koordinatensystem an. |
| Zeile 26: | Zeile 26: | ||
| − | 1. Zuerst stellen wir | + | 1. Zuerst stellen wir $y$ in der Ungleichung frei: |
| − | $$2x-y\ | + | $$2x-y\geq -1 \ \ \vert -2x$$ |
| − | $$-y\ | + | $$-y\geq -2x-1 \ \ \vert \cdot (-1)$$ |
| − | : Achtung | + | : Achtung: Bei der Multiplikation und Division mit negativen Zahlen ändert sich das Ungleichheitszeichen! (siehe [[Ungleichung]]) |
| − | $$y\ | + | $$y\leq 2x+1$$ |
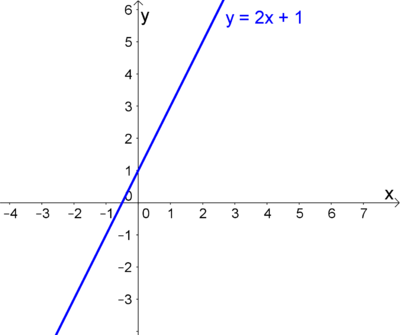
2. Nun zeichnen wir zuerst die Gerade für $y=2x+1$ (siehe [[lineare Funktionen]]) | 2. Nun zeichnen wir zuerst die Gerade für $y=2x+1$ (siehe [[lineare Funktionen]]) | ||
| Zeile 37: | Zeile 37: | ||
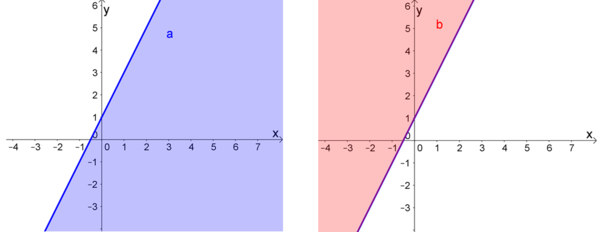
3. Wir wissen, dass die Lösungsmenge eine der Halbebenen oberhalb oder unterhalb der Geraden ist. Diese zwei Fälle sind möglich: | 3. Wir wissen, dass die Lösungsmenge eine der Halbebenen oberhalb oder unterhalb der Geraden ist. Diese zwei Fälle sind möglich: | ||
[[Datei:bsp1c.png|thumb|center|600px|1. Möglichkeit: untere Halbebene $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ 2. Möglichkeit: obere Halbebene ]] | [[Datei:bsp1c.png|thumb|center|600px|1. Möglichkeit: untere Halbebene $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ 2. Möglichkeit: obere Halbebene ]] | ||
| − | Um herauszufinden, welche dieser Halbebenen die richtige ist, gibt es nun 2 Möglichkeiten: | + | |
| + | <br /> | ||
| + | Um herauszufinden, welche dieser Halbebenen die richtige ist, gibt es nun $2$ Möglichkeiten: | ||
'''a) Einsetzen eines beliebigen Punktes auf einer der Halbebenen in die Ungleichung'''<br /> | '''a) Einsetzen eines beliebigen Punktes auf einer der Halbebenen in die Ungleichung'''<br /> | ||
| − | Hierzu nehmen wir einen beliebigen Punkt (z.B. | + | Hierzu nehmen wir einen beliebigen Punkt (z. B. $(0,0)$ oder $(1,4)$) und überprüfen, ob dieser Punkt die Ungleichung $y\geq 2x+1$ erfüllt. Dies geschieht, indem wir ihn in die Ungleichung einsetzen. |
| − | Erhalten wir eine wahre Aussage, so liegt der Punkt auf der entsprechenden Halbebene. Erhalten wir eine falsche Aussage, so liegt der Punkt nicht auf der Halbebene womit die Lösungsmenge die Halbebene gegenüber vom Punkt sein muss. | + | Erhalten wir eine wahre Aussage, so liegt der Punkt auf der entsprechenden Halbebene. Erhalten wir eine falsche Aussage, so liegt der Punkt nicht auf der Halbebene, womit die Lösungsmenge die Halbebene gegenüber vom Punkt sein muss. |
| Zeile 49: | Zeile 51: | ||
{| border=1 | {| border=1 | ||
|- | |- | ||
| − | !Einsetzen von (0,0) in $y\ | + | !Einsetzen von $(0,0)$ in $y\leq 2x+1$ ein !! Einsetzen von $(1,4)$ in $y\leq 2x+1$ ein |
|- | |- | ||
| $$y\leq 2x+1$$ | | $$y\leq 2x+1$$ | ||
| Zeile 55: | Zeile 57: | ||
$$0\leq 0+1$$ | $$0\leq 0+1$$ | ||
$$ 0\leq 1\ \textrm{wahre Aussage}$$ | $$ 0\leq 1\ \textrm{wahre Aussage}$$ | ||
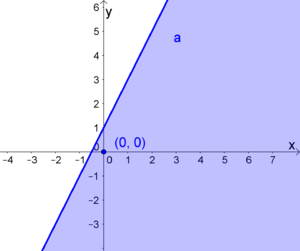
| − | Somit liegt der Punkt (0,0) in der Halbebene. Dadurch wissen wir, dass die untere Halbebene die Lösungsmenge sein muss. | + | Somit liegt der Punkt $(0,0)$ in der Halbebene. Dadurch wissen wir, dass die untere Halbebene die Lösungsmenge sein muss. |
| − | [[Datei:Bsp1d.png|thumb|center|Das Einsetzen des Punktes (0,0) führt zu einer wahren Aussage. Somit muss (0,0) auf der Halbebene liegen.]] | + | [[Datei:Bsp1d.png|thumb|center|Das Einsetzen des Punktes $(0,0)$ führt zu einer wahren Aussage. Somit muss $(0,0)$ auf der Halbebene liegen.]] |
| $$y\leq 2x+1$$ | | $$y\leq 2x+1$$ | ||
$$4 \leq 2\cdot 1+1$$ | $$4 \leq 2\cdot 1+1$$ | ||
$$4\leq 2+1$$ | $$4\leq 2+1$$ | ||
$$ 4\leq 3\ \textrm{falsche Aussage}$$ | $$ 4\leq 3\ \textrm{falsche Aussage}$$ | ||
| − | Somit liegt der Punkt (1,4) '''NICHT''' in der Halbebene. Dadurch wissen wir, dass die untere Halbebene die Lösungsmenge sein muss. | + | Somit liegt der Punkt $(1,4)$ '''NICHT''' in der Halbebene. Dadurch wissen wir, dass die untere Halbebene die Lösungsmenge sein muss. |
| − | [[Datei:Bsp1e.png|thumb|center|Das Einsetzen des Punktes (1,4) führt zu einer falschen Aussage. Somit kann (1,4) nicht auf der Halbebene liegen.]] | + | [[Datei:Bsp1e.png|thumb|center|Das Einsetzen des Punktes $(1,4)$ führt zu einer falschen Aussage. Somit kann $(1,4)$ nicht auf der Halbebene liegen.]] |
|} | |} | ||
| Zeile 70: | Zeile 72: | ||
# Selbstverständlich reicht es, nur einen Punkt in die Ungleichung einzusetzen. | # Selbstverständlich reicht es, nur einen Punkt in die Ungleichung einzusetzen. | ||
# Achte darauf, dass der eingesetzte Punkt nicht auf der Geraden liegt! Er sollte immer eindeutig in einer der beiden Halbebenen liegen. | # Achte darauf, dass der eingesetzte Punkt nicht auf der Geraden liegt! Er sollte immer eindeutig in einer der beiden Halbebenen liegen. | ||
| + | |||
| + | <br /> | ||
'''b) Richtiges Deuten des Ungleichheitszeichens''' | '''b) Richtiges Deuten des Ungleichheitszeichens''' | ||
| − | Die Ungleichung $y\leq 2x+1$ bedeutet, dass die y- | + | Anstelle des Einsetzens eines Punktes, können wir auch durch richtiges Deuten des Ungleichheitszeichens die entsprechende Halbebene herausfinden: <br /> |
| + | |||
| + | Die Ungleichung $y\leq 2x+1$ bedeutet, dass die $y$-Koordinate (= vertikale Koordinate) immer kleiner oder gleich dem Wert $2x+1$ sein muss. Somit muss die $y$-Koordinate immer unterhalb der Geraden sein. Demzufolge muss die gesuchte Halbebene unterhalb der Geraden sein. | ||
| Zeile 79: | Zeile 85: | ||
</div> | </div> | ||
| − | |||
| − | |||
{{Vorlage:Merke|1= | {{Vorlage:Merke|1= | ||
Methode zum Skizzieren der Lösungsmenge:<br /> | Methode zum Skizzieren der Lösungsmenge:<br /> | ||
| − | '''1. Schritt:''' Forme die Ungleichungen zuerst nach y um. Beachte dabei, dass sich die Richtung des Ungleichheitszeichens bei der Multiplikation und Division mit negativen Zahlen ändert. | + | '''1. Schritt:''' Forme die Ungleichungen zuerst nach $y$ um. Beachte dabei, dass sich die Richtung des Ungleichheitszeichens bei der Multiplikation und Division mit negativen Zahlen ändert. |
| + | |||
<br /> | <br /> | ||
| + | |||
'''2. Schritt:''' Zeichne nun zuerst die Gerade der [[Lineare Funktionen | linearen Funktion]] in das Koordinatensystem. Beachte dabei, dass | '''2. Schritt:''' Zeichne nun zuerst die Gerade der [[Lineare Funktionen | linearen Funktion]] in das Koordinatensystem. Beachte dabei, dass | ||
| − | :: bei <,> die Gerade | + | :: bei $<,>$ die Gerade gestrichelt gezeichnet wird und |
:: bei $\leq, \geq$ die Gerade ganz normal durchgehend gezeichnet wird. | :: bei $\leq, \geq$ die Gerade ganz normal durchgehend gezeichnet wird. | ||
<br /> | <br /> | ||
| Zeile 94: | Zeile 100: | ||
:: bei $<$ oder $\leq$ ist es die untere Halbebene/linke Halbebene und | :: bei $<$ oder $\leq$ ist es die untere Halbebene/linke Halbebene und | ||
:: bei $>$ oder $\geq$ ist es die obere Halbebene/rechte Halbebene. | :: bei $>$ oder $\geq$ ist es die obere Halbebene/rechte Halbebene. | ||
| − | + | Alternativ kannst du auch einen Punkt des Koordinatensystems in die Ungleichung einsetzen und überprüfen, ob dieser auf der Halbebene liegt. <br /> | |
| − | + | '''Wichtig:''' Der Punkt darf NICHT auf der Geraden liegen! | |
}} | }} | ||
| − | {{Vorlage:Beispiel|1= Gib die Lösungsmengen der folgenden 3 Ungleichungen graphisch an. Zeichne dabei die Lösung jeder Ungleichung | + | {{Vorlage:Beispiel|1= Gib die Lösungsmengen der folgenden $3$ Ungleichungen graphisch an. Zeichne dabei die Lösung jeder Ungleichung in ein separates Koordinatensystem:<br /> |
| + | <br /> | ||
<br /> | <br /> | ||
| + | a) $\quad y\geq 0$<br /> | ||
| − | + | b) $\quad 3x+2y\leq 50$<br /> | |
| − | + | c) $\quad x<15$<br /> | |
| − | + | d) $\quad y<10$ | |
| − | + | ||
| − | d) $y<10$ | + | |
|2= | |2= | ||
'''1. Schritt:''' Umformen der Ungleichungen (falls nötig): | '''1. Schritt:''' Umformen der Ungleichungen (falls nötig): | ||
| − | + | Von den angeführten Beispielen muss nur b) $3x+2y\leq 50$ umgeformt werden:<br /> | |
| − | + | ||
| − | + | a) $\quad y\geq 0$ <br /> | |
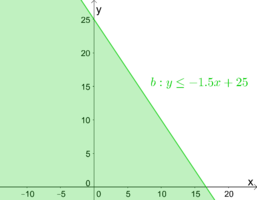
| − | + | b) $\quad 3x+2y\leq 50 \rightarrow 2y\leq -3x+50 \rightarrow$ '''$y\leq -\frac{3}{2}x+25$''' <br /> | |
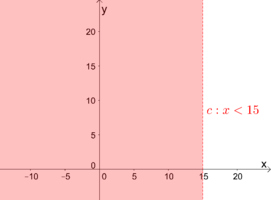
| − | d) $y<10$ | + | c) $\quad x<15$<br /> |
| + | |||
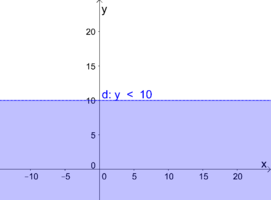
| + | d) $\quad y<10$ | ||
<br /> | <br /> | ||
| − | |||
'''2. Schritt:''' Zeichnen der Geraden | '''2. Schritt:''' Zeichnen der Geraden | ||
<gallery widths="300px" heights="200"> | <gallery widths="300px" heights="200"> | ||
| − | Bsp2a1.png|a) Die Gerade $y=0$ ist waagrecht und schneidet die y-Achse bei 0. | + | Bsp2a1.png|a) Die Gerade $y=0$ ist waagrecht und schneidet die $y$-Achse bei $0$. |
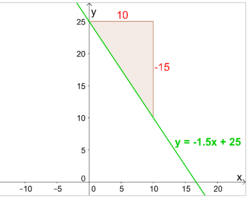
Bsp2b1.png|b) Die Gerade $y=-\frac{3}{2}x+25$ wird mithilfe des Steigungsdreieckes eingezeichnet. | Bsp2b1.png|b) Die Gerade $y=-\frac{3}{2}x+25$ wird mithilfe des Steigungsdreieckes eingezeichnet. | ||
| − | Bsp2c1.png|c) $x=15$ ist eine senkrechte Gerade, die bei 15 die x-Achse schneidet. | + | Bsp2c1.png|c) $x=15$ ist eine senkrechte Gerade, die bei $15$ die $x$-Achse schneidet. |
| − | Bsp2d1.png|d) Die Gerade $y=10$ ist parallel zur x-Achse und schneidet bei 10 die y-Achse. | + | Bsp2d1.png|d) Die Gerade $y=10$ ist parallel zur $x$-Achse und schneidet bei $10$ die $y$-Achse. |
</gallery> | </gallery> | ||
| − | '''3. Schritt:''' Ermitteln der entsprechenden Halbebene durch Einsetzen eines Punktes (der Punkt (1,1) | + | '''3. Schritt:''' Ermitteln der entsprechenden Halbebene durch Einsetzen eines Punktes (der Punkt $(1,1)$ eignet sich hier für alle Ungleichungen) oder durch Beachten des Ungleichheitszeichens: |
<gallery widths="300px" heights="200"> | <gallery widths="300px" heights="200"> | ||
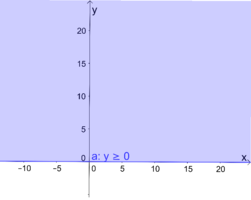
Bsp2a2.png|a) Aufgrund des $\geq$ ist die obere Halbebene der Lösungsbereich. | Bsp2a2.png|a) Aufgrund des $\geq$ ist die obere Halbebene der Lösungsbereich. | ||
| Zeile 147: | Zeile 153: | ||
}} | }} | ||
| − | == | + | == Weitere Aufgaben == |
| − | * [http:// | + | |
| + | * [http://ne.lo-net2.de/selbstlernmaterial/m/s1al/lug/lugindex.html Materialien zum selbstständigen Arbeiten (Thomas Unkelbach)] | ||
= Ungleichungssysteme = | = Ungleichungssysteme = | ||
== Ungleichungssysteme == | == Ungleichungssysteme == | ||
{{Definition| | {{Definition| | ||
| − | [[Datei:Unglsys-intro.png|thumb|right| | + | [[Datei:Unglsys-intro.png|thumb|right|280px|Die Lösungsmenge eines Ungleichungssystems ist der „Überlappungsbereich“ aller Ungleichungen.]] |
Ein Ungleichungssystem besteht aus mehreren Ungleichungen. | Ein Ungleichungssystem besteht aus mehreren Ungleichungen. | ||
| − | Die Lösungsmenge eines | + | Die Lösungsmenge eines Ungleichungssystems ist jener Bereich, der alle Ungleichungen erfüllt. |
| − | Graphisch ist dies jener | + | Graphisch ist dies jener „Überlappungsbereich“, der auf allen Halbebenen liegt.}} |
{{#ev:youtube|UhqsciDyYdg}} | {{#ev:youtube|UhqsciDyYdg}} | ||
| Zeile 164: | Zeile 171: | ||
{{Vorlage:Beispiel|1= | {{Vorlage:Beispiel|1= | ||
Gib die Lösungsmenge des folgenden Ungleichungssystems graphisch an: | Gib die Lösungsmenge des folgenden Ungleichungssystems graphisch an: | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
$$I:\ y\geq 0$$ | $$I:\ y\geq 0$$ | ||
$$II:\ 3x+2y\leq 50 $$ | $$II:\ 3x+2y\leq 50 $$ | ||
| Zeile 171: | Zeile 181: | ||
Anschließend markieren wir jenen Bereich, der von allen Ungleichungen überlappt wird. | Anschließend markieren wir jenen Bereich, der von allen Ungleichungen überlappt wird. | ||
| − | Das folgende Applet zeigt dir diese 2 Schritte: | + | Das folgende Applet zeigt dir diese $2$ Schritte: |
<ggb_applet width="990" height="550" version="5.0" id="Yavd6grD" /> | <ggb_applet width="990" height="550" version="5.0" id="Yavd6grD" /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 193: | Zeile 193: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
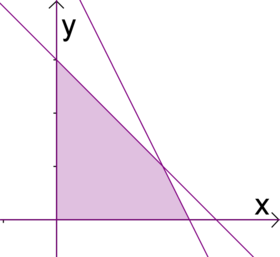
| + | Antwort: Der Lösungsbereich ist somit jene unendlich große Fläche, der von allen $3$ Ungleichungen begrenzt wird. | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | '''Zusammenfassung''' | ||
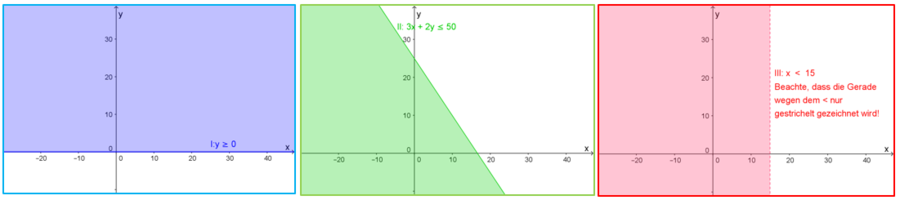
| + | [[Datei:Unglsys-Bsp-einzelabbildungen.png|thumb|center|900px|Zuerst zeichnet man die Lösungsmenge jeder einzelnen Ungleichung. Wenn du dies selbst machst, achte darauf, dass du alle Ungleichungen in EIN Koordinatensystem zeichnest!]] | ||
| + | |||
| + | |||
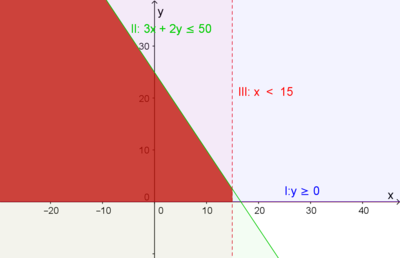
| + | [[Datei:Unglsys-bsp-überlappungsbereich.png|thumb|center|400px|Legt man nun alle Halbebenen übereinander, so erhält man den dunkelroten Überlappungsbereich.]] | ||
| + | |||
}} | }} | ||
| Zeile 200: | Zeile 207: | ||
== Textaufgaben, die zu Ungleichungssystemen führen == | == Textaufgaben, die zu Ungleichungssystemen führen == | ||
{{Vorlage:Merke|1= Ungleichungssysteme können auch in Form von Textaufgaben vorliegen. Um eine solche Aufgabe zu lösen, geht man wie folgt vor: | {{Vorlage:Merke|1= Ungleichungssysteme können auch in Form von Textaufgaben vorliegen. Um eine solche Aufgabe zu lösen, geht man wie folgt vor: | ||
| − | # Definiere die Unbekannten x bzw. y. | + | # Definiere die Unbekannten $x$ bzw. $y$. |
# Stelle mithilfe des Textes alle Ungleichungen auf. | # Stelle mithilfe des Textes alle Ungleichungen auf. | ||
# Zeichne in ein Koordinatensystem die Lösungsmenge jeder Ungleichung und markiere anschließend den Überlappungsbereich.}} | # Zeichne in ein Koordinatensystem die Lösungsmenge jeder Ungleichung und markiere anschließend den Überlappungsbereich.}} | ||
| Zeile 211: | Zeile 218: | ||
<br /> | <br /> | ||
| − | *Für einen Liter der Sorte | + | *Für einen Liter der Sorte „Fruchtgenuss“ braucht er $2 kg$ Äpfel und $1 kg$ Trauben. |
| − | *Für einen Liter der Sorte | + | *Für einen Liter der Sorte „Happy fruits“ braucht er je ein $kg$ Äpfel und Trauben. |
| − | Insgesamt hat Raimund 5 kg Äpfel und 3 kg Trauben. | + | *Insgesamt hat Raimund $5 kg$ Äpfel und $3 kg$ Trauben. |
<br /> | <br /> | ||
| − | + | a) $\ $ Raimund will wissen, wie viele Liter jeder Sorte er herstellen kann. Stelle dazu das zugehörige Ungleichungssystem auf. <br /> | |
| − | + | b) $\ $ Ermittle graphisch jenen Bereich, der Raimunds mögliche Produktionsmengen angibt. <br /> | |
| − | a) Raimund will wissen, wie viele Liter jeder Sorte er herstellen kann. Stelle dazu das zugehörige Ungleichungssystem auf. <br /> | + | c) $\ $ Begründe, ob es für Raimund möglich ist, einen Liter „Fruchtgenuss“ und $2.5$ Liter „Happy fruits“ zu produzieren?<br /> |
| − | b) Ermittle graphisch jenen Bereich, der Raimunds mögliche Produktionsmengen angibt. <br /> | + | d) $\ $ Gib zwei mögliche Produktionsmengen für die beiden Sorten an. |
| − | c) Begründe, ob es für Raimund möglich ist, einen Liter | + | |
| − | d) Gib zwei mögliche Produktionsmengen für die beiden Sorten an. | + | |
<br> | <br> | ||
| Zeile 232: | Zeile 237: | ||
'''a) Raimund will wissen, wie viele Liter jeder Sorte er herstellen kann. Stelle dazu alle zugehörigen Ungleichungen auf.'''<br /> | '''a) Raimund will wissen, wie viele Liter jeder Sorte er herstellen kann. Stelle dazu alle zugehörigen Ungleichungen auf.'''<br /> | ||
| − | Zuerst definieren wir die Unbekannten x und y. Da wir wissen wollen, wie viele Liter er von jeder Sorte herstellen kann ist <br /> | + | Zuerst definieren wir die Unbekannten $x$ und $y$. Da wir wissen wollen, wie viele Liter er von jeder Sorte herstellen kann, ist <br /> |
| − | x... Anzahl der Liter Fruchtgenuss<br /> | + | $x$... Anzahl der Liter Fruchtgenuss<br /> |
| − | y... Anzahl der Liter Happy fruits | + | $y$... Anzahl der Liter Happy fruits |
| − | Nun stellen wir die zugehörigen Ungleichungen auf. Eine mögliche Hilfe kann das | + | Nun stellen wir die zugehörigen Ungleichungen auf. Eine mögliche Hilfe kann das Erstellen einer Tabelle sein: |
{| border=1 align=center | {| border=1 align=center | ||
|- | |- | ||
| − | ! $\ $ !!$$x | + | ! $\ $ !!$$x \; \textrm{Fruchtgenuss}$$ !! $$y \; \textrm{Happy fruits}$$ !! Maximum |
|- | |- | ||
| − | | Äpfel in kg || 2 || 1 || $\leq 5$ | + | | Äpfel in $kg$ || $$2$$ || $$1$$ || $$\leq 5$$ |
|- | |- | ||
| − | | Trauben in kg || 1 || 1 || $\leq 3$ | + | | Trauben in $kg$ || $$1$$ || $$1$$ || $$\leq 3$$ |
|} | |} | ||
| + | |||
Daraus lassen sich nun einfach die Ungleichungen herauslesen: | Daraus lassen sich nun einfach die Ungleichungen herauslesen: | ||
| Zeile 254: | Zeile 260: | ||
Selbstverständlich gilt auch, dass $x$ und $y$ nur positiv sein dürfen, da wir ja nicht negative Liter herstellen können, somit erhalten wir das folgende Ungleichungssystem: | Selbstverständlich gilt auch, dass $x$ und $y$ nur positiv sein dürfen, da wir ja nicht negative Liter herstellen können, somit erhalten wir das folgende Ungleichungssystem: | ||
| + | <br /> | ||
$$I: x\geq 0$$ | $$I: x\geq 0$$ | ||
$$II: y\geq 0$$ | $$II: y\geq 0$$ | ||
| Zeile 263: | Zeile 270: | ||
'''b) Ermittle graphisch jenen Bereich, der Raimunds mögliche Produktionsmengen angibt.''' <br /> | '''b) Ermittle graphisch jenen Bereich, der Raimunds mögliche Produktionsmengen angibt.''' <br /> | ||
| − | Hierzu formen wir zuerst alle Ungleichungen auf y um. | + | Hierzu formen wir zuerst alle Ungleichungen auf $y$ um. |
| − | + | <br /> | |
| − | $II: y\geq 0$ | + | $$I: x\geq 0$$ |
| − | + | $$II: y\geq 0$$ | |
| − | $III: 2x+y\leq 5\ \ \rightarrow y\leq -2x+5$ | + | $$III: 2x+y\leq 5\ \ \rightarrow y\leq -2x+5$$ |
| − | + | $$IV: x+y\leq 3\ \ \ \rightarrow y\leq -x+3$$ | |
| − | $IV: x+y\leq 3\ \ \ \rightarrow y\leq -x+3$ | + | |
| − | Dann zeichnen wir die Geraden ein und markieren jenen Bereich, der auf allen 4 Halbebenen liegt und erhalten: | + | Dann zeichnen wir die Geraden ein und markieren jenen Bereich, der auf allen $4$ Halbebenen liegt und erhalten: |
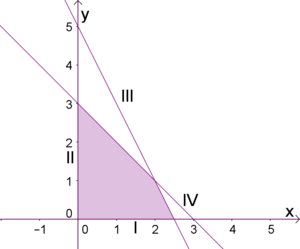
[[Datei:Unglsys-textbsp.png|thumb|center|Die Lösungsmenge eines Ungleichunggsystems ist der Überlappungsbereich aller Ungleichungen.]] | [[Datei:Unglsys-textbsp.png|thumb|center|Die Lösungsmenge eines Ungleichunggsystems ist der Überlappungsbereich aller Ungleichungen.]] | ||
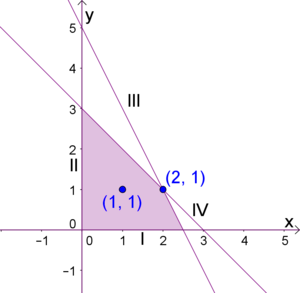
| − | Der rot markierte Bereich gibt uns nun alle möglichen | + | Der rot markierte Bereich gibt uns nun alle möglichen Produktionsmengen an. |
| − | '''c) Begründe, ob es für Raimund möglich ist, einen Liter | + | '''c) Begründe, ob es für Raimund möglich ist, einen Liter „Fruchtgenuss“ und $2.5$ Liter „Happy fruits“ zu produzieren?'''<br /> |
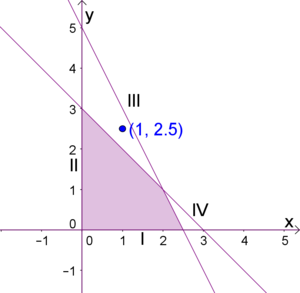
| − | Antwort: Es ist nicht möglich x=1 Liter | + | Antwort: Es ist nicht möglich $x=1$ Liter „Fruchtgenuss“ und $y=2.5$ Liter „Happy fruits“ zu produzieren, da der Punkt $(1,2.5)$ nicht in der Lösungsmenge liegt. |
[[Datei:Unglsys-textbsp2.png|thumb|center|300px|Der Punkt (1,2.5) liegt nicht im Planungsfeld.]] | [[Datei:Unglsys-textbsp2.png|thumb|center|300px|Der Punkt (1,2.5) liegt nicht im Planungsfeld.]] | ||
| − | '''Hinweis:''' Eine alternative Argumentation wäre gewesen, dass wir nicht genug Trauben zur Verfügung haben. Raimund bräuchte hier nämlich insgesamt 3.5 kg Trauben. | + | '''Hinweis:''' Eine alternative Argumentation wäre gewesen, dass wir nicht genug Trauben zur Verfügung haben. Raimund bräuchte hier nämlich insgesamt $3.5 kg$ Trauben. |
| Zeile 292: | Zeile 298: | ||
[[Datei:Unglsys-textbsp3.png|thumb|center|300px]] | [[Datei:Unglsys-textbsp3.png|thumb|center|300px]] | ||
| − | + | Z. B.: | |
| − | * Punkt (1,1): Ein Liter | + | * Punkt $(1,1)$: Ein Liter „Fruchtgenuss“ und ein Liter „Happy fruits“. |
| − | * Punkt (2,1): Ein Liter | + | * Punkt $(2,1)$: Ein Liter „Fruchtgenuss“ und ein Liter „Happy fruits“. |
</div> | </div> | ||
| Zeile 300: | Zeile 306: | ||
</div> | </div> | ||
| − | = | + | = Interaktive Übungen = |
| − | == | + | |
| − | + | ||
| + | == Quiz: Lineare Ungleichungen (AG 2.4) == | ||
| + | |||
| + | {{#widget:Iframe | ||
| + | |url= https://h5p.org/h5p/embed/755433 | ||
| + | |width= 90% | ||
| + | |height= 850 | ||
| + | |border=1 | ||
| + | }} | ||
| + | <br> | ||
| + | |||
| + | = Weitere Aufgaben = | ||
| + | ==Online-Übungen== | ||
* [http://www.mathe-trainer.de/Klasse8/Ungleichungssysteme/Block1/Aufgaben.htm Aufgaben auf mathe-trainer.de (Teil 1)] | * [http://www.mathe-trainer.de/Klasse8/Ungleichungssysteme/Block1/Aufgaben.htm Aufgaben auf mathe-trainer.de (Teil 1)] | ||
* [http://www.mathe-trainer.de/Klasse8/Ungleichungssysteme/Block2/Aufgaben.htm Aufgaben auf mathe-trainer.de (Teil 2)] | * [http://www.mathe-trainer.de/Klasse8/Ungleichungssysteme/Block2/Aufgaben.htm Aufgaben auf mathe-trainer.de (Teil 2)] | ||
| − | = | + | = Weiterführende Themen = |
| − | + | ||
| + | |||
| + | {| border=1 | ||
| + | |- | ||
| + | | [[Datei:Planungsfeld u Zielfkt5.gif|200px|center|link=Lineare Optimierung]] | ||
| + | | [[Lineare Optimierung]] | ||
| + | |} | ||
| + | |||
| + | [[Kategorie: Algebra und Geometrie]] | ||