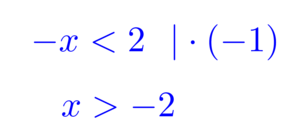Ungleichung

Ungleichung

• Ungleichungen mit einer Variable
• Ungleichungen mit zwei Variablen

Definition

Im Gegensatz zu einer Gleichung hat eine Ungleichung anstelle des Gleichheitszeichens ($=$) eines der folgenden $4$ Ungleichheitszeichen: $<$... (eindeutig/echt) kleiner $\leq $... kleiner oder gleich $>$... (eindeutig/echt) größer $\geq$... größer oder gleich

Beispiele:

• $5<3$
• $2x+3 \geq 11$

Angabe der Lösungsmenge

Die Lösungsmenge von Ungleichungen können wir auf drei verschiedene Arten angeben:

Graphisch am Zahlenstrahl

Geben wir die Lösungsmenge graphisch an, so markieren wir all jene Werte, die die Ungleichung erfüllen, auf dem Zahlenstrahl.

Geben Sie die Lösungsmenge der folgenden Ungleichung graphisch an.


a) $x<2$
b) $x\geq -2.5$
c) $-2.5\leq x<2$

$x<2$	$x\geq -2.5$	$-2.5\leq x <2$
Alle Zahlen kleiner als $2$ sind eine Lösung für $x$. Die Zahl zwei gehört gerade nicht mehr zur Lösung. Aus diesem Grund zeichnen wir bei $2$ einen offenen Kreis ein. Graphische Lösungsmenge für $x<2$	Alle Zahlen größer gleich $-2.5$ gehören zur Lösung. Da $-2.5$ zur Lösung gehört, malen wir hier einen vollen (geschlossenen) Punkt. Graphische Lösungsmenge für $-2.5\leq x$	Die Lösungsmenge befindet sich zwischen $-2.5$ und $2$. Da $-2.5$ zur Lösung gehört, zeichnen wir hier einen geschlossenen Punkt. Dagegen gehört $2$ wegen dem $<$ nicht mehr zur Lösung, weshalb wir hier einen offenen Punkt einzeichnen. Graphische Lösungsmenge für $-2.5\leq x<2$

Merke

$\\ $ Gehört ein Punkt gerade noch zur Lösungsmenge, so malen wir einen vollen (geschlossenen) Punkt aus. Gehört ein Punkt GERADE NICHT MEHR zur Lösungsmenge, so malen wir einen offenen Punkt.

Intervallschreibweise

Merke

Wir unterscheiden zwischen $3$ Arten von Intervallen: Das geschlossene Intervall $[a,b]$ beinhaltet alle Zahlen zwischen den Grenzen $a$ und $b$, wobei $a$ und $b$ im Intervall liegen. Das offene Intervall $(a,b)$ bzw. $]a,b[$ beinhaltet alle Zahlen zwischen den Grenzen $a$ und $b$, wobei $a$ und $b$ NICHT im Intervall liegen. Das halboffene Intervall $[a,b)$ bzw. $[a,b[$ oder $(a,b]$ bzw. $]a,b]$ beinhaltet alle Zahlen zwischen den Grenzen $a$ und $b$, wobei jeweils nur eine der beiden Grenzen im Intervall liegt. Hinweis: $(a,b)$ und $]a,b[$ sind zwei Schreibweisen für dasselbe offene Intervall.

Geben Sie die Lösungsmenge der folgenden Ungleichung als Intervall an.


a) $x<2$
b) $x\geq -2.5$
c) $-2.5\leq x<2$

a) $x<2\rightarrow$ Intervall: $(-\infty;2)$

in Worten: alle Zahlen zwischen $-\infty$ und $2$, wobei $2$ nicht mehr zur Lösung gehört.

b) $x\geq -2.5\rightarrow$ Intervall: $ [-2.5;\infty)$

c) $-2.5\leq x<2 \rightarrow$ Intervall: $ [-2.5;2)$
in Worten: alle Zahlen zwischen $-2.5$ und $2$, wobei die Grenze $2$ nicht zur Lösung gehört.

Mengenschreibweise

Die Mengenschreibweise ist die einfachste Darstellung der Lösungsmenge, da sie nur die Grundmenge und die (vereinfachte) Ungleichung angibt, wie an folgenden Musterbeispielen leicht zu erkennen ist:

Geben Sie die Lösungsmenge der folgenden Ungleichung in der Mengenschreibweise an.


a) $x<2$
b) $x\geq -2.5$
c) $-2.5\leq x<2$

a) $x<2\rightarrow$ Lösungsmenge: $\mathbb{L}=\{x\in \mathbb{R}\vert x<2\}$

in Worten: „die Lösungsmenge beinhaltet alle reellen Zahlen $x$, die kleiner als $2$ sind.“

b) $x\geq -2.5\rightarrow$ Lösungsmenge: $ \mathbb{L}=\{x\in \mathbb{R}\vert x\geq -2.5\} $

c) $-2.5\leq x<2 \rightarrow$ Lösungsmenge: $\mathbb{L}=\{x\in \mathbb{R}\vert -2.5\leq x<2\}$
in Worten: „die Lösungsmenge beinhaltet alle reellen Zahlen $x$, die größer gleich $-2.5$ und kleiner als $2$ sind.“

Lösung von Ungleichungen mit einer Variable

Eine lineare Ungleichung löst man ähnlich wie eine Gleichung mithilfe von Umformungen:

Löse die Ungleichung $3x+1<7$ über der Grundmenge der reellen Zahlen $\mathbb{R}$.

$$3x+1<7 \ \ \vert -1$$ $$3x<6 \ \ \vert :3$$ $$x<2$$

Lösungsmenge:

graphisch	Intervall	Mengenschreibweise
graphische Darstellung der Lösungsmenge für $x<2$	$$\ ( -\infty ;2)\ \hspace{1em} \text{oder} \hspace{1em} ]-\infty ;2[ $$	$$\mathbb{L}=\{x\in \mathbb{R}\vert x<2\}$$

Merke

Der wichtigste Unterschied beim Umformen zwischen Gleichung und Ungleichung: Wird eine Ungleichung mit einer negativen Zahl multipliziert oder dividiert, so ändert sich die Richtung des Ungleichungszeichens!

Hinweis!

Beweisidee:

Nehmen wir die Ungleichung $$3<5$$ und multiplizieren wir links und rechts mit $(-1)$: $$3<5 \ \ \vert \cdot (-1)$$ $$-3\ \color{red}{?} -5\ \ \ $$ Damit die Ungleichung immer noch stimmt, muss man nun das Ungleichungszeichen ändern, weil $-3$ größer ist als $-5$ (schau dir das am Zahlenstrahl an!) $$-3>-5$$ Somit hat sich das Ungleichungszeichen umgedreht!

Bestimme die Lösungsmenge der Ungleichung $$\frac{15-3x}{-2}\geq 2x-7$$ über der Grundmenge der reellen Zahlen $\mathbb{R}$.

$$\frac{15-3x}{-2}\geq 2x-7$$ Zuerst lösen wir den Bruch auf, indem wir mit $(-2)$ multiplizieren: $$\frac{15-3x}{-2}\geq 2x-7\ \ \ \vert \cdot (-2)$$ $$15-3x\leq -4x+14\ \ \ \ \ \ \ $$ Beachte, dass sich das Ungleichungszeichen gedreht hat!

Nun bringen wir alle $x$ auf eine Seite: $$15-3x\leq -4x+14 \ \ \ \vert +4x\ \hspace{0.5em} \vert -15$$ $$x\leq -1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $$

Lösungsmenge:

graphisch	Intervall	Mengenschreibweise
graphische Darstellung der Lösung für $x\leq -1$	$$\ (-\infty ;-1]\ \hspace{1em} \text{oder} \hspace{1em} ]-\infty;1]$$	$$\mathbb{L}=\{x\in \mathbb{R}\vert x\leq -1\}$$

Fallunterscheidung bei Multiplikation mit $x$

folgt in Kürze

Ungleichungssysteme mit einer Variablen

folgt in Kürze

Übungsaufgaben

Online-Übungen

• Aufgaben auf mathe-online.at

Quiz: Ungleichungen (AG 2.4)

Siehe:

Lineare Ungleichungen mit 2 Variablen