Potenz- und Polynomfunktionen
Inhaltsverzeichnis
Potenzfunktionen - Allgemeines
|
Eine Potenzfunktion ist eine Funktion der Form $f(x)=a\cdot x^n \ \textrm{mit} \ n\in \mathbb{Q}$. |
Wenn man den Schieberegler bewegt, kann man erkennen, dass Potenzfunktionen für verschiedene Hochzahlen $n$ zum Teil sehr unterschiedliche Graphen liefern.
Um die Eigenschaften der Potenzfunktionen genauer zu untersuchen, ist es hilfreich, die Potenzfunktionen Kategorien einzuteilen, die dieselben Eigenschaften haben:
- Potenzfunktionen mit natürlichen Exponenten $n \in \mathbb{N}$
- Exponent ungerade
- Exponent gerade
- Potenzfunktionen mit negativen ganzzahligen Exponenten
- Exponent ungerade
- Exponent gerade
- Potenzfunktionen mit „echt rationalen“ Exponenten - Wurzelfunktionen
Graphen von Potenzfunktionen
Je nach Größe der Parameter $a$ und $n$ verändert sich der Graph. Im Folgenden werden die Auswirkungen der einzelnen Parameter auf den Graphen der Funktion besprochen:
$$f(x)=a\cdot x^n$$
Bedeutung der Hochzahl $n$ für den Funktionsgraphen
Um die Bedeutung des Hochzahl $n$ für den Funktionsgraphen zu verstehen, lassen wir vorerst den Wert von $a$ konstant bei $1$ ($f(x)=x^n$).
| Potenzfunktionen mit ungeraden natürlichen Exponenten | |
| In diesem Fall ist der Graph monoton steigend. Je größer $n$ ist, desto mehr „schmiegt“ sich die Funktion im Bereich $[-1;1]$ der $x$-Achse an. Im gesamten übrigen Bereich steigt die Funktion hingegen stärker. Für negative $x$-Werte sind auch die zugehörigen Funktionswerte negativ. Diese Potenzfunktionen haben immer genau eine reelle Nullstelle bei $x=0$. | 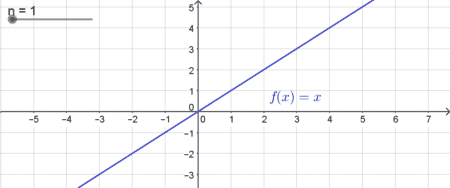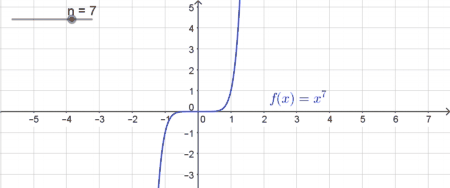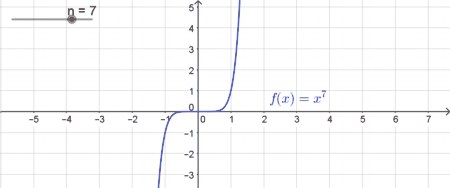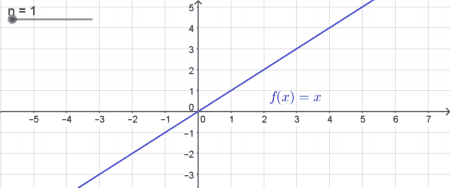
|
| Potenzfunktionen mit geraden natürlichen Exponenten | |
| In diesem Fall ist der Graph im Intervall $] - \infty ; 0]$ monoton fallend und im Intervall $[0; \infty[ $ monoton steigend. Der Graph nimmt nur positive Funktionswerte an („Minus mal Minus ergibt Plus“). Für $n=2$ nennt man den Funktionsgraph eine Parabel (siehe Quadratische Funktionen). Auch dieser Typ von Potenzfunktionen hat genau eine reelle Nullstelle bei $x=0$. | 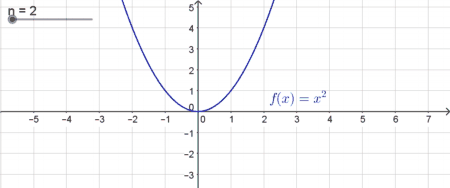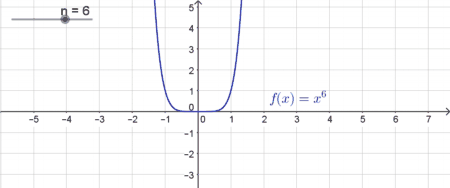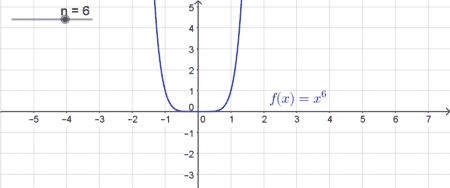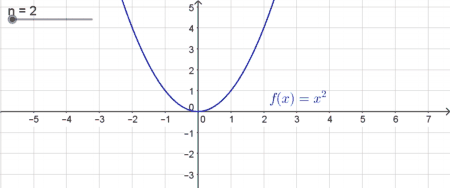
|
| Potenzfunktionen mit ungeraden negativen Exponenten | |
| In diesem Fall ist der Graph sowohl im Intervall $] - \infty ; 0[$ monoton fallend als auch im Intervall $[0; \infty[ $ monoton fallend. Die Funktion ist für $x=0$ nicht definiert, was sich durch die alternative Schreibweise $f(x)=x^{-n} = \frac{1}{x^n}$ (siehe Potenzregeln leicht erklären lässt, da es bei $x=0$ zu einer Division durch Null kommen würde. Deshalb besteht an der Stelle $x=0$ eine sogenannte „Sprungstelle“. Der Graph nähert sich im negativen und im positiven Bereich immer mehr der $x$-Achse, berührt diese jedoch nie. Es gibt somit keine reellen Nullstellen. | 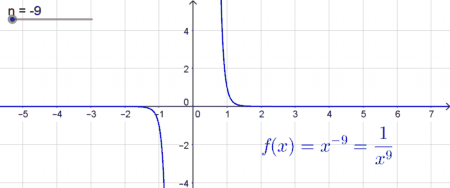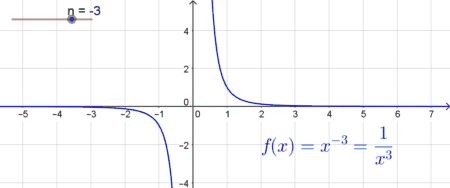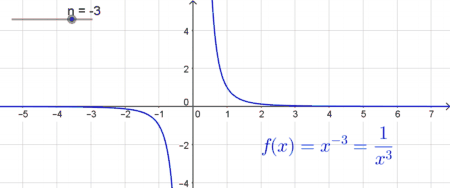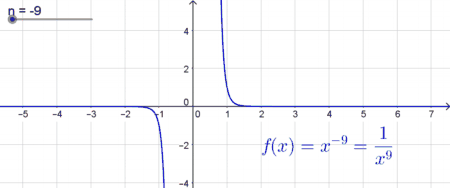
|
| Potenzfunktionen mit geraden negativen Exponenten | |
| In diesem Fall ist der Graph im Intervall $] - \infty ; 0[$ monoton steigend und im Intervall $[0; \infty[ $ monoton fallend. Auch diese Funktion ist für $x=0$ nicht definiert und es gibt an der Stelle $x=0$ wiederum eine „Sprungstelle“. Der Graph nimmt nur positive Funktionswerte an, da beispielsweise $f(x)=x^{-2}$ auch als $ \frac{1}{x^2}$ geschrieben werden kann und $x^2$ stets positive Werte liefert („Minus mal Minus ergibt Plus“). Der Graph nähert sich im negativen und im positiven Bereich immer mehr der $x$-Achse, berührt diese jedoch nie. Es gibt somit keine reellen Nullstellen. | 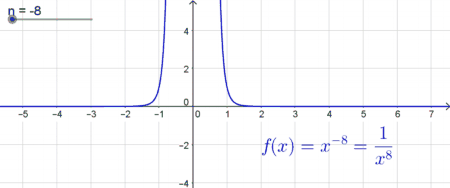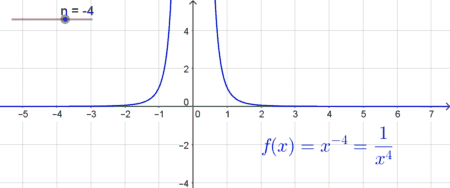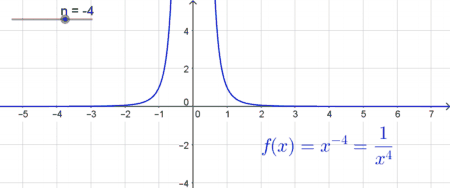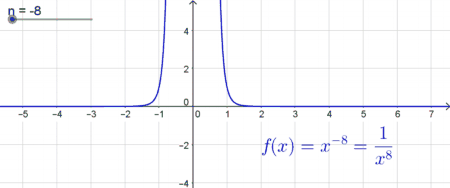
|
| Potenzfunktionen mit „echt rationalen“ Exponenten | |
| Diese Funktionen können aufgrund der Rechenregeln Potenzregeln auch als Wurzelfunktionen angeschrieben werden: $\sqrt[n]{x^m}=x^{\frac{m}{n} }$. Wir beschränken uns hier auf die Diskussion der Quadratwurzelfunktion: $\sqrt{x}=x^{\frac{1}{2} }$.
Die (Quadrat-)Wurzelfunktion ist nur für $ \mathbb{R}_0^+$ definiert. Sie ist im gesamten Intervall $[0; \infty[ $ monoton steigend. Die Steigung des Graphen ist am Anfang sehr groß, nimmt jedoch immer mehr ab. Die Steigung bleibt jedoch stets $>0$. Es gibt genau eine reelle Nullstelle bei $x=0$. |
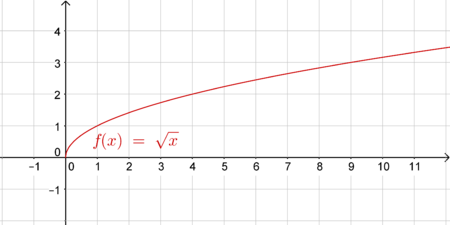
|
Füge im folgenden Applet zu jeder Graphik die passende Funktion hinzu.
Bedeutung des Parameters $a$ für den Funktionsgraphen
Das folgende GeoGebra-Applet soll dir helfen, die Bedeutung des Parameters $a$ zu verstehen.
Aufgabenstellungen zum Applet
- Untersuche, wie sich eine Änderung des Vorzeichens des Parameters $a$ auf den Funktionsgraphen auswirkt. Variiere dazu den Schieberegler von $a$. Begründe, warum sich der Graph so verändert.
- Stelle den Wert von $n$ nun auf $1$. Gib an, um welchen speziellen Funktionstyp es sich hier handelt und was der Wert von $a$ angibt.
- Stelle den Wert von $n$ nun auf $2$. Beobachte, wie sich die Veränderung von $a$ auf den Funktionsgraphen auswirkt.
Lösungen zu den Aufgabenstellungen
- Eine Änderung des Vorzeichens bewirkt eine Spiegelung des Funktionsgraphen. Exemplarische Begründung: Angenommen die ursprüngliche Funktion ist $f(x)= 2 \cdot x^3$. Die Vorzeichenänderung führt zur Funktionsgleichung $f(x)= -2 \cdot x^3$. Das Minus macht also nichts anderes, als das Vorzeichen eines jeden Funktionswertes „umzudrehen“.
- Funktionen der Form $f(x)= a \cdot x$ sind lineare Funktionen, bei denen $d=0$ ist. Der Parameter $a$ gibt somit die Steigung der Geraden an.
- Wie du sicher bemerkt hast, handelt es sich hier um einen einfachen Fall von quadratischen Funktionen. Eine ausführliche Erklärung, wie sich die Veränderung des Parameters auf den Funktionsgraphen auswirkt, findest du hier.
Füge im folgenden Applet zu jeder Graphik die passende Funktion hinzu.
Inhaltsverzeichnis
Polynomfunktionen
|
Polynomfunktionen sind Funktionen, die aus Potenzfunktionen mit natürlichen Exponenten zusammengesetzt sind. Die allgemeine Funktionsgleichung einer Polynomfunktion lautet:
$$f(x)=a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+a_{n-2}\cdot x^{n-2} +\dots + a_1\cdot x^1 + a_0\ \ \textrm{mit } a_i \in \mathbb{R}, 0\leq i\leq n$$ oder in Kurzschreibweise: $$f(x)=\sum_{i=0}^n a_i \cdot x^i \ \textrm{mit } a_i \in \mathbb{R}$$
|
Beispiel:
- für eine Polynomfunktion 3. Grades (kubische Funktion): $f(x)=2\cdot x^3+x^2+3\cdot x+5$
- für eine Polynomfunktion 2. Grades (quadratische Funktion): $f(x)=x^2+2x-5$
Verwende im folgenden GeoGebra-Applet Schieberegler um verschiedene Polynomfunktionen zu erzeugen:
Das Applet zeigt, dass Polynomfunktionen sehr verschiedenartig aussehen können. Um etwas Ordnung in die „Polynoms-Vielfalt“ zu bringen, werden wir uns jeweils die wichtigsten Gemeinsamkeiten der Polynomfunktionen eines bestimmten „Grades“ genauer anschauen:
Polynomfunktionen vom Grad $1$
| Allgemeine Gleichung: $f(x)=a_1 \cdot x + a_0$ |
| In diesem Fall ist der Graph eine lineare Funktion. Bei diesen Funktionen werden anstatt der Variablen $a_1$ und $a_0$ meist $k$ und $d$ verwendet. Genaue Details zu den Eigenschaften linearer Funktionen findest du im Kapitel lineare Funktionen.
Aufgabe: Stelle im obigen GeoGebra-Applet die Schieberegler von $a_4$, $a_3$ und $a_2$ auf Null und überzeuge dich davon, dass du stets eine lineare Funktion erhältst. |
Polynomfunktionen vom Grad $2$
| Allgemeine Gleichung: $f(x)=a_2 \cdot x^2 + a_1 \cdot x + a_0 $ |
| In diesem Fall ist der Graph eine quadratische Funktion. Genaue Details findest du im Kapitel quadratische Funktionen.
Aufgabe: Stelle im obigen GeoGebra-Applet die Schieberegler von $a_4$ und $a_3$ auf Null und überzeuge dich davon, dass du stets eine quadratische Funktion erhältst. Variiere nun die Schieberegler von $a_2$, $a_1$ und $a_0$ um unterschiedliche Funktionsgraphen zu erzeugen. |
Polynomfunktionen vom Grad $3$
| Allgemeine Gleichung: $f(x)=a_3 \cdot x^3 + a_2 \cdot x^2 + a_1 \cdot x + a_0 $ |
| Aufgabe: Stelle im obigen GeoGebra-Applet die Schieberegler von $a_4$ auf Null ($a_3 \neq 0$) um eine Polynomfunktion vom Grad drei zu erhalten. Variiere nun die Schieberegler von $a_3$, $a_2$, $a_1$ und $a_0$ um unterschiedliche Funktionsgraphen zu erzeugen. |
| Polynomfunktionen vom Grad $3$ haben stets mindestens eine Nullstelle. |
Polynomfunktionen vom Grad $4$
| Allgemeine Gleichung: $f(x)=a_4 \cdot x^4 + a_3 \cdot x^3 + a_2 \cdot x^2 + a_1 \cdot x + a_0 $ |
| Aufgabe: Stelle im obigen GeoGebra-Applet die Schieberegler von $a_4 \neq 0$ um eine Polynomfunktion vom Grad vier zu erhalten. Variiere nun die Schieberegler um unterschiedliche Funktionsgraphen zu erzeugen. |
Nullstellen von Polynomfunktionen
- Die Anzahl der möglichen Nullstellen kann sehr einfach abgeschätzt werden: Eine Polynomfunktion vom Grad $n$ hat maximal $n$ Nullstellen. Das heißt, dass z. B. eine Polynomfunktion vom Grad $3$ maximal $3$ reelle Nullstellen haben kann.
- Polynomfunktionen vom Grad $1, 3, 5, ...$ haben stets mindestens eine reelle Nullstelle.
- Polynomfunktionen vom Grad $2, 4, 6, ...$ müssen nicht unbedingt eine reelle Nullstelle haben. Es kann z. B. sein, dass bei einer Funktion vom Grad $2$ der Graph der Parabel nach oben verschoben ist (Bsp.: $f(x)=x^2+2$) und die $x$-Achse somit nicht geschnitten wird.
- Um Nullstellen einer Funktion zu berechnen muss $f(x)=0$ gesetzt werden. Bei Polynomfunktionen vom Grad $2$ können die Lösungsformeln angewandt werden um die Gleichung zu lösen.
Hat die Polynomfunktion einen höheren Grad ($n>2$), müssen spezielle Formeln angewandt oder der Grad der Funktion mithilfe einer Polynomdivision „heruntergedrückt“ werden. Hierzu versucht man durch geschicktes Probieren eine ganzzahlige Nullstelle zu erraten und dividiert das ursprüngliche Polynom durch die Differenz $(x-Nullstelle)$. Dadurch erhält man ein neues Polynom, das einfacher gelöst werden kann (z. B. mithilfe einer Lösungsformel).
- Manchmal können Polynomfunktionen auch als Produkt von Linearfaktoren angegeben werden. In diesem Fall können die Nullstellen besonders einfach abgelesen werden.
Beispiel: $$f(x)=x²+x-6=(x-2) \cdot (x+3)$$ Berechnung der Nullstellen: $0=x²+x-6$ bzw. $0=(x-2) \cdot (x+3)$ In der linken Form kann die kleine Lösungsformel eingesetzt werden, um die Nullstellen zu berechnen. Durch Einsetzen in die Formel erhält man $x_1=2, \ x_2=-3$. Ist die Gleichung in der rechten Form (Produkt von Linearfaktoren) gegeben, so können die Nullstellen im Kopf berechnet bzw. abgelesen werden: Damit das Produkt von $(x-2) \cdot (x+3)$ Null ergibt, muss entweder $(x-2)$ oder $(x+3)$ gleich Null sein. Hier kommen nur $x_1=2$ und $x_2=-3$ in Frage.
Bestimme die Nullstellen der Funktion $f(x)=x^2 \cdot (x+2)^2$:
$$0=x^2 \cdot (x+2)^2$$
Damit das Produkt Null wird, muss entweder $x^2$ oder $(x+2)^2$ Null sein.
Somit gibt es nur zwei reelle Nullstellen: $x_1=0$ und $x_2=-2$ (siehe Abb.)
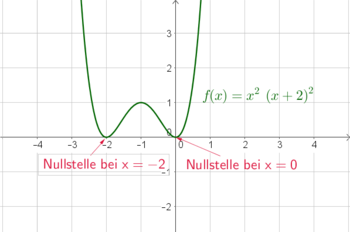
Würde man den Term ausmultiplizieren und versuchen die Nullstellen des erhaltenen Polynoms (vom Grad $4$) zu berechnen, wäre das deutlich aufwändiger.
Anmerkung zur Theorie: Vielfachheit von Nullstellen
Im vorangegangenen Beispiel hatten wir eine Polynomfunktion vom Grad $4$, weshalb wir maximal $4$ Nullstellen erwarten können. Die Nullstellen $x_1=0$ und $x_2=-2$ kommen jedoch „doppelt“ vor. Man sagt dazu, dass sie die „Vielfachheit“ $2$ haben. Woran erkennt man die „Vielfachheit“ einer Nullstelle?
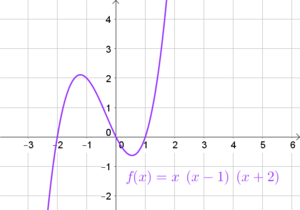
- Vielfachheit 1: Der Linearfaktor kommt einfach vor. Bsp.: $f(x)=x \cdot (x-1) \cdot (x+2)$ hat drei Nullstellen der Vielfachheit 1 ($x_1=0, \ x_2=1, \ x_3=-2$).
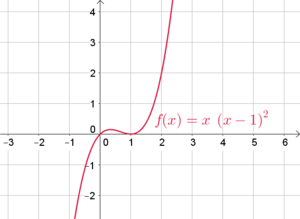
- Vielfachheit 2: Ein Linearfaktor kommt doppelt („zum Quadrat“) vor. Bsp.: $f(x)=x \cdot (x-1)^2$ hat eine Nullstelle mit Vielfachheit 1 ($x_1=0$) und eine Nullstelle mit Vielfachheit 2 ($x_2=1$). Die Vielfachheit 2 erkennt man daran, dass die Funktion die $x$-Achse nur berührt und nicht schneidet.
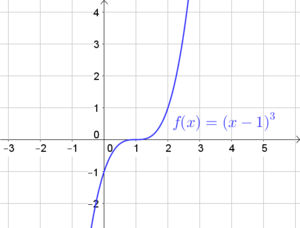
- Vielfachheit 3: Ein Linearfaktor kommt dreifach („hoch drei“) vor. Bsp.: $f(x)=(x-1)^3$ hat genau eine Nullstelle mit Vielfachheit 3 ($x_1=1$).
- Auch die anderen Vielfachheiten können einfach an den Hochzahlen der Linearfaktoren erkannt werden.
Der Begriff Vielfachheit ist etwas verwirrend, da wir eine doppelte Nullstelle graphisch nur als eine Stelle sehen.
Interaktive Übungen
|
Sollten die Aufgaben nicht korrekt dargestellt werden, lade die Seite noch einmal, indem du $F5$ drückst oder ganz oben im Browser auf „Aktualisieren“ |
Quiz: Potenzfunktionen (FA 3.1-3.3)
Quiz: Polynomfunktionen (FA 4.1-4.4)
Tipp: Orientiere dich am Grad der Funktion, den Nullstellen und evtl. dem absoluten Glied $a_0$.