Inhalt:Integration: Weg, Geschwindigkeit, Beschleunigung: Unterschied zwischen den Versionen
Aus Matura Wiki
(→Beispiele) |
(→Beispiele) |
||
| Zeile 27: | Zeile 27: | ||
{{Vorlage:Beispiel|1= | {{Vorlage:Beispiel|1= | ||
Die ESA (European Space Agency) bringt mithilfe der Ariane 5 regelmäßig Satelliten in den Weltraum. Die Startbeschleunigung beträgt dabei ca. $5.5 m/s^2$. Gehen Sie im Folgenden davon aus, dass die Beschleunigung während des ganzen Fluges konstant ist (d. h. $a(t)=5.5 m/s^2$). Die Variable $t$ gebe die Zeit nach dem Start in Sekunden ($s$) an. | Die ESA (European Space Agency) bringt mithilfe der Ariane 5 regelmäßig Satelliten in den Weltraum. Die Startbeschleunigung beträgt dabei ca. $5.5 m/s^2$. Gehen Sie im Folgenden davon aus, dass die Beschleunigung während des ganzen Fluges konstant ist (d. h. $a(t)=5.5 m/s^2$). Die Variable $t$ gebe die Zeit nach dem Start in Sekunden ($s$) an. | ||
| − | |||
::::a) Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$) | ::::a) Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$) | ||
| − | |||
::::b) Bestimmen Sie mithilfe von $v$ die Funktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | ::::b) Bestimmen Sie mithilfe von $v$ die Funktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | ||
| − | |||
::::c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia). | ::::c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia). | ||
:::::Berechnen Sie: | :::::Berechnen Sie: | ||
:::::* die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet. | :::::* die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet. | ||
:::::* die Geschwindigkeit der Rakete zu diesem Zeitpunkt. | :::::* die Geschwindigkeit der Rakete zu diesem Zeitpunkt. | ||
| − | |||
::::d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. | ::::d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. | ||
| − | |||
|2= | |2= | ||
| Zeile 49: | Zeile 44: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$v(t)=\int a(t) \cdot dt$$ | $$v(t)=\int a(t) \cdot dt$$ | ||
| Zeile 57: | Zeile 51: | ||
'''Antwort:''' Die Geschwindigkeitsfunktion lautet $v(t)=5.5 \cdot t$. | '''Antwort:''' Die Geschwindigkeitsfunktion lautet $v(t)=5.5 \cdot t$. | ||
| − | |||
| − | |||
b) Bestimmen Sie mithilfe von $v$ die Wegfunktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | b) Bestimmen Sie mithilfe von $v$ die Wegfunktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | ||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| Zeile 68: | Zeile 59: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$s(t)=\int v(t) \cdot dt$$ | $$s(t)=\int v(t) \cdot dt$$ | ||
| Zeile 74: | Zeile 64: | ||
$$s(t)=5.5 \cdot \frac{t^2}{2} +c$$ | $$s(t)=5.5 \cdot \frac{t^2}{2} +c$$ | ||
$$s(t)=2.75 \cdot t^2$$ | $$s(t)=2.75 \cdot t^2$$ | ||
| − | |||
'''Antwort:''' Die Funktionsgleichung lautet $s(t)=2.75 \cdot t^2$. | '''Antwort:''' Die Funktionsgleichung lautet $s(t)=2.75 \cdot t^2$. | ||
| − | |||
| − | |||
c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia). | c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia). | ||
| − | Berechnen Sie | + | Berechnen Sie ... |
| − | + | ||
| − | + | ||
| − | + | ||
| + | - ... die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet. | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| − | |||
<div class="mw-collapsible-content"> $s(t)$ ist die Formel der zurückgelegten Strecke. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wo sich die Rakete nach $180$ Sekunden befindet. | <div class="mw-collapsible-content"> $s(t)$ ist die Formel der zurückgelegten Strecke. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wo sich die Rakete nach $180$ Sekunden befindet. | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
| − | |||
$$s(t)=2.75 \cdot t^2$$ | $$s(t)=2.75 \cdot t^2$$ | ||
$$s(180)=2.75 \cdot 180^2$$ | $$s(180)=2.75 \cdot 180^2$$ | ||
$$s(180)=89 100 m$$ | $$s(180)=89 100 m$$ | ||
| − | |||
'''Antwort:''' Nach $180$ Sekunden befindet sich unsere Rakete in einer Höhe von $89 100 m$. | '''Antwort:''' Nach $180$ Sekunden befindet sich unsere Rakete in einer Höhe von $89 100 m$. | ||
| − | |||
| − | |||
[[Datei:Weg Geschwindigkeit Zeit Grafik (Christina Felder).png|miniatur|]] | [[Datei:Weg Geschwindigkeit Zeit Grafik (Christina Felder).png|miniatur|]] | ||
| − | |||
| − | |||
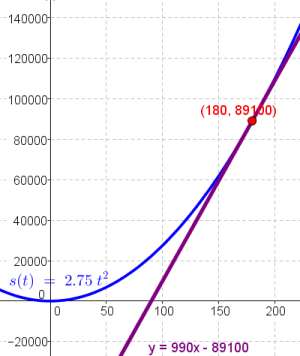
[[Datei:C.png|miniatur|Das $k$ der Tangente gibt die Geschwindigkeit an.]] | [[Datei:C.png|miniatur|Das $k$ der Tangente gibt die Geschwindigkeit an.]] | ||
| − | |||
| + | - ... die Geschwindigkeit der Rakete zu diesem Zeitpunkt. | ||
| Zeile 118: | Zeile 95: | ||
$v(t)$ ist die Formel, die die Geschwindigkeit zum Zeitpunkt $t$ angibt. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wie hoch die Geschwindigkeit der Rakete nach $180$ Sekunden ist. Das Ergebnis erscheint in $m/s$. Wenn das Ergebnis in $km/h$ gewünscht wäre, müsste man das Ergebnis noch mal $3.6$ rechnen. | $v(t)$ ist die Formel, die die Geschwindigkeit zum Zeitpunkt $t$ angibt. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wie hoch die Geschwindigkeit der Rakete nach $180$ Sekunden ist. Das Ergebnis erscheint in $m/s$. Wenn das Ergebnis in $km/h$ gewünscht wäre, müsste man das Ergebnis noch mal $3.6$ rechnen. | ||
}} | }} | ||
| − | |||
| Zeile 130: | Zeile 106: | ||
'''Antwort:''' Nach $180$ Sekunden hat unsere Rakete eine Geschwindigkeit von $3 564 km/h$ erreicht. | '''Antwort:''' Nach $180$ Sekunden hat unsere Rakete eine Geschwindigkeit von $3 564 km/h$ erreicht. | ||
| − | |||
| − | |||
d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. | d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. | ||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| Zeile 142: | Zeile 115: | ||
Wichtig ist hierbei, dass $s(t)$ den Weg in $m$ angibt! </div> | Wichtig ist hierbei, dass $s(t)$ den Weg in $m$ angibt! </div> | ||
</div> | </div> | ||
| − | |||
| − | |||
$$1 000 000=2.75 \cdot t^2$$ | $$1 000 000=2.75 \cdot t^2$$ | ||
$$t=603.02$$ | $$t=603.02$$ | ||
<br /> | <br /> | ||
| − | |||
'''Antwort:''' Nach $603.02$ Sekunden erreichen wir mit unserer Rakete die Höhe $1 000 000$ Meter. | '''Antwort:''' Nach $603.02$ Sekunden erreichen wir mit unserer Rakete die Höhe $1 000 000$ Meter. | ||
| Zeile 176: | Zeile 146: | ||
'''Antwort:''' Die Funktion lautet $$v(t)=7.94 \cdot t$$. | '''Antwort:''' Die Funktion lautet $$v(t)=7.94 \cdot t$$. | ||
| − | |||
| − | |||
b) Bestimmen Sie mithilfe der Geschwindigkeitsfunktion $v(t)$ die Funktion $s(t)$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | b) Bestimmen Sie mithilfe der Geschwindigkeitsfunktion $v(t)$ die Funktion $s(t)$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | ||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| Zeile 187: | Zeile 154: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$v(t)= 7.94 \cdot t (+c)$$ | $$v(t)= 7.94 \cdot t (+c)$$ | ||
| Zeile 194: | Zeile 160: | ||
$$s(t)=7.94 (t^2)/2 + c \cdot t$$ | $$s(t)=7.94 (t^2)/2 + c \cdot t$$ | ||
$$s(t)=3.97 \cdot t^2 (+ c \cdot t)$$ | $$s(t)=3.97 \cdot t^2 (+ c \cdot t)$$ | ||
| − | |||
'''Antwort:''' Die Funktion lautet: $$s(t)=3.97 \cdot t^2 (+ c \cdot t)$$ | '''Antwort:''' Die Funktion lautet: $$s(t)=3.97 \cdot t^2 (+ c \cdot t)$$ | ||
| − | |||
c) Berechnen Sie ... | c) Berechnen Sie ... | ||
| − | |||
- ... die zurückgelegte Distanz nach $300$ Sekunden. | - ... die zurückgelegte Distanz nach $300$ Sekunden. | ||
| Zeile 209: | Zeile 172: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$s(300)= 3.9t \cdot 300^2 (+c \cdot t)$$ | $$s(300)= 3.9t \cdot 300^2 (+c \cdot t)$$ | ||
$$s(300)= 357 300 m$$ | $$s(300)= 357 300 m$$ | ||
| − | |||
- ... die Geschwindigkeit zu diesem Zeitpunkt. | - ... die Geschwindigkeit zu diesem Zeitpunkt. | ||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| Zeile 223: | Zeile 183: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$v(300)= 7.94 \cdot 300 (+c)$$ | $$v(300)= 7.94 \cdot 300 (+c)$$ | ||
| Zeile 230: | Zeile 189: | ||
$2 382 m/s \rightarrow 661.67 km/h$ | $2 382 m/s \rightarrow 661.67 km/h$ | ||
| − | |||
| − | |||
d) Nach $2 000 km$ erreicht das Raumschiff den Mars. Ermitteln Sie, nach wie vielen Sekunden das Raumschiff den Mars erreicht. | d) Nach $2 000 km$ erreicht das Raumschiff den Mars. Ermitteln Sie, nach wie vielen Sekunden das Raumschiff den Mars erreicht. | ||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| Zeile 241: | Zeile 197: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$2 000 000=3.97 \cdot t^2$$ | $$2 000 000=3.97 \cdot t^2$$ | ||
$$t = 709.77 Sek.$$ | $$t = 709.77 Sek.$$ | ||
| − | |||
$709.77 s \rightarrow 11.83 min$ | $709.77 s \rightarrow 11.83 min$ | ||
| Zeile 254: | Zeile 208: | ||
*[http://www.brinkmann-du.de/physik/ph_aufgaben/phob_a02/phob_a02.htm Beispiele mit Lösungen von brinkmann-du] | *[http://www.brinkmann-du.de/physik/ph_aufgaben/phob_a02/phob_a02.htm Beispiele mit Lösungen von brinkmann-du] | ||
| − | + | *[http://learningapps.org/watch?v=per6zao0n01 Ordne die Ableitungen der richtigen Stammfunktion zu.] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | http://learningapps.org/watch?v=per6zao0n01 | + | |
Version vom 24. Januar 2021, 19:08 Uhr
Begriffe
Wird die Geschwindigkeit $v$ durch den Graphen angegeben, so ist die Steigung die Beschleunigung $a$. Der Flächeninhalt unter $v$ gibt den Weg $s$ an.
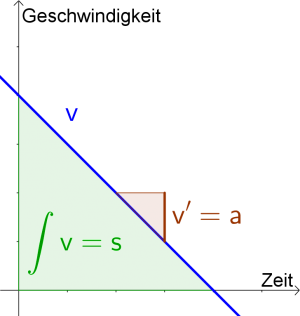
- $s(t)$ gibt den zurückgelegten Weg zum Zeitpunkt $t$ an (Einheit: $m$ oder $km$ ...)
- $v(t)$ gibt die Momentangeschwindigkeit zum Zeitpunkt $t$ an (Einheit: $m/s$ oder $km/h$ ...). Die Geschwindigkeit ist die momentane Änderung des Weges $s(t)$, d. h.
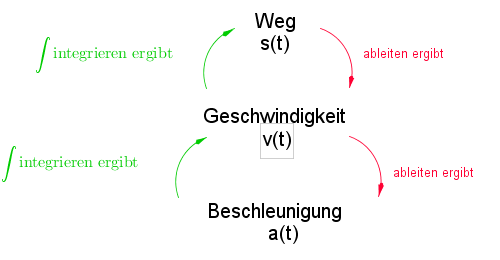
$$s'(t)=v(t)\textrm{ bzw. } \int v(t)=s(t)+c,\textrm{ wobei $c$ die Anfangsstrecke $s_0$ angibt.}$$
- $a(t)$ gibt die Beschleunigung zum Zeitpunkt $t$ an (Einheit: $m/s^2$ oder $km/h^2$ ...). Die Beschleunigung ist die momentane Änderung der Geschwindigkeit $v(t)$, d. h.
$$v'(t)=a(t)\textrm{ bzw. } \int a(t)=v(t)+c,\textrm{ wobei $c$ die Anfangsgeschwindigkeit $v_0$ angibt.}$$
Vereinfacht gesagt gilt folgender Zusammenhang:
Beispiele
Die ESA (European Space Agency) bringt mithilfe der Ariane 5 regelmäßig Satelliten in den Weltraum. Die Startbeschleunigung beträgt dabei ca. $5.5 m/s^2$. Gehen Sie im Folgenden davon aus, dass die Beschleunigung während des ganzen Fluges konstant ist (d. h. $a(t)=5.5 m/s^2$). Die Variable $t$ gebe die Zeit nach dem Start in Sekunden ($s$) an.
- a) Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$)
- b) Bestimmen Sie mithilfe von $v$ die Funktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt.
- c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia).
- Berechnen Sie:
- die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet.
- die Geschwindigkeit der Rakete zu diesem Zeitpunkt.
- Berechnen Sie:
- d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird.
a) Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$)
Tipp zur Berechnung:
Da die Funktion der Geschwindigkeit $v(t)$ gesucht wird, müssen wir die Formel der Beschleunigung $a(t)$ einmal integrieren. Wir setzen $5.5$ (Dies entnehmen wir aus der Angabe) für $a(t)$ ein und berechnen $v(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=v_0$ wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ beträgt und damit $v(0)=0$ gelten muss.
$$v(t)=\int a(t) \cdot dt$$ $$v(t)=\int 5.5 \cdot dt$$ $$v(t)=5.5 \cdot t + v_0$$ $$v(t)=5.5 \cdot t$$
Antwort: Die Geschwindigkeitsfunktion lautet $v(t)=5.5 \cdot t$.
b) Bestimmen Sie mithilfe von $v$ die Wegfunktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt.
Tipp zur Berechnung:
Da die Funktion des Weges $s$ gesucht wird, müssen wir die Formel der Geschwindigkeit $v(t)$ einmal integrieren. Wir setzen $5.5t$ (dies entnehmen wir aus dem Ergebnis von Aufgabe a) für $v(t)$ ein und berechnen so unser Ergebnis für $s(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=s_0$ wegfällt, da unsere zurückgelegte Strecke zu Beginn $0$ ist.
$$s(t)=\int v(t) \cdot dt$$ $$s(t)=\int 5.5t \cdot dt$$ $$s(t)=5.5 \cdot \frac{t^2}{2} +c$$ $$s(t)=2.75 \cdot t^2$$
Antwort: Die Funktionsgleichung lautet $s(t)=2.75 \cdot t^2$.
c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia).
Berechnen Sie ...
- ... die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet.
$s(t)$ ist die Formel der zurückgelegten Strecke. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wo sich die Rakete nach $180$ Sekunden befindet.
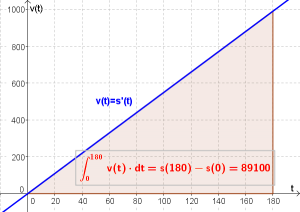
$$s(t)=2.75 \cdot t^2$$ $$s(180)=2.75 \cdot 180^2$$ $$s(180)=89 100 m$$
Antwort: Nach $180$ Sekunden befindet sich unsere Rakete in einer Höhe von $89 100 m$.
.png)
- ... die Geschwindigkeit der Rakete zu diesem Zeitpunkt.
Tipp zur Berechnung:
$v(t)$ ist die Formel, die die Geschwindigkeit zum Zeitpunkt $t$ angibt. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wie hoch die Geschwindigkeit der Rakete nach $180$ Sekunden ist. Das Ergebnis erscheint in $m/s$. Wenn das Ergebnis in $km/h$ gewünscht wäre, müsste man das Ergebnis noch mal $3.6$ rechnen.
$$v(t)=5.5 \cdot t$$
$$v(180)=5.5 \cdot 180$$
$$v(180)=990 m/s$$
$$990 m/s \rightarrow 3 564 km/h$$
Antwort: Nach $180$ Sekunden hat unsere Rakete eine Geschwindigkeit von $3 564 km/h$ erreicht.
d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird.
Tipp zur Berechnung:
Die Funktion $s$ beschreibt den zurückgelegten Weg. Wenn wir die unrealistische Annahme voraussetzen, dass die Rakete „kerzengerade“ emporsteigt, müssen wir somit berechnen, wann $s(t)=1000 km=1 000 000 m$ beträgt.
Wichtig ist hierbei, dass $s(t)$ den Weg in $m$ angibt!
$$1 000 000=2.75 \cdot t^2$$
$$t=603.02$$
Antwort: Nach $603.02$ Sekunden erreichen wir mit unserer Rakete die Höhe $1 000 000$ Meter.
