Inhalt:Integration: Weg, Geschwindigkeit, Beschleunigung: Unterschied zwischen den Versionen
Aus Matura Wiki
(→Begriffe) |
(→Beispiele) |
||
| Zeile 26: | Zeile 26: | ||
==Beispiele== | ==Beispiele== | ||
{{Vorlage:Beispiel|1= | {{Vorlage:Beispiel|1= | ||
| − | Die ESA (European Space Agency) bringt mithilfe der Ariane 5 regelmäßig Satelliten in den Weltraum. | + | Die ESA (European Space Agency) bringt mithilfe der Ariane 5 regelmäßig Satelliten in den Weltraum. Die Startbeschleunigung beträgt dabei ca. $5.5 m/s^2$. Gehen Sie im Folgenden davon aus, dass die Beschleunigung während des ganzen Fluges konstant ist (d. h. $a(t)=5.5 m/s^2$). Die Variable $t$ gebe die Zeit nach dem Start in Sekunden ($s$) an. |
| − | Die Startbeschleunigung beträgt dabei ca. 5.5 m/ | + | |
| − | Gehen Sie im Folgenden davon aus, dass die Beschleunigung | + | |
| − | Die Variable t gebe die Zeit nach dem Start in Sekunden (s) an. | + | |
<br> | <br> | ||
<br> | <br> | ||
| − | '''a)'''Bestimmen Sie die Funktion v, die die Geschwindigkeit der Rakete nach t Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit v(0)=v_0=0) | + | '''a)'''Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$) |
<br> | <br> | ||
<br> | <br> | ||
| − | '''b)''' Bestimmen Sie mithilfe von v die Funktion s, die den nach t Sekunden zurückgelegten Weg angibt. | + | '''b)''' Bestimmen Sie mithilfe von $v$ die Funktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt. |
<br> | <br> | ||
<br> | <br> | ||
| − | '''c)''' 180 Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia). | + | '''c)''' $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia). |
Berechnen Sie: | Berechnen Sie: | ||
:* die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet. | :* die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet. | ||
| − | :* die Geschwindigkeit der Rakete zu diesem Zeitpunkt | + | :* die Geschwindigkeit der Rakete zu diesem Zeitpunkt. |
<br> | <br> | ||
| − | '''d)''' In etwa 1000 km Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. | + | '''d)''' In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. |
| − | + | ||
| − | + | ||
| Zeile 54: | Zeile 49: | ||
|2= | |2= | ||
| − | + | '''a)'''Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$) | |
| − | '''a)'''Bestimmen Sie die Funktion v, die die Geschwindigkeit der Rakete nach t Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit v(0)=v_0=0) | + | |
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Da die Funktion der Geschwindigkeit v(t) gesucht wird, müssen wir die Formel der Beschleunigung a(t) einmal integrieren. Wir setzen 5 | + | <div class="mw-collapsible-content"> Da die Funktion der Geschwindigkeit $v(t)$ gesucht wird, müssen wir die Formel der Beschleunigung $a(t)$ einmal integrieren. Wir setzen $5.5$ (Dies entnehmen wir aus der Angabe) für $a(t)$ ein und berechnen $v(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=v_0$ wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ beträgt und damit $v(0)=0$ gelten muss. |
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$v(t)=\int a(t) \cdot dt$$ | $$v(t)=\int a(t) \cdot dt$$ | ||
| − | $$v(t)=\int 5 | + | $$v(t)=\int 5.5 \cdot dt$$ |
| − | $$v(t)=5 | + | $$v(t)=5.5 \cdot t + v_0$$ |
| − | $$v(t)=5 | + | $$v(t)=5.5 \cdot t$$ |
| − | + | ||
| − | + | ||
| + | '''Antwort''': Die Geschwindigkeitsfunktion lautet $v(t)=5.5 \cdot t$. | ||
| − | |||
| + | '''b)''' Bestimmen Sie mithilfe von $v$ die Wegfunktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Da die Funktion des Weges s gesucht wird, müssen wir die Formel der Geschwindigkeit v(t) einmal integrieren. Wir setzen 5 | + | <div class="mw-collapsible-content"> Da die Funktion des Weges $s$ gesucht wird, müssen wir die Formel der Geschwindigkeit $v(t)$ einmal integrieren. Wir setzen $5.5t$ (dies entnehmen wir aus dem Ergebnis von Aufgabe a) für $v(t)$ ein und berechnen so unser Ergebnis für $s(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=s_0$ wegfällt, da unsere zurückgelegte Strecke zu Beginn $0$ ist. |
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$s(t)=\int v(t) \cdot dt$$ | $$s(t)=\int v(t) \cdot dt$$ | ||
| − | $$s(t)=\int 5 | + | $$s(t)=\int 5.5t \cdot dt$$ |
| − | $$s(t)=5 | + | $$s(t)=5.5 \cdot \frac{t^2}{2} +c$$ |
| − | $$s(t)=2 | + | $$s(t)=2.75 \cdot t^2$$ |
| − | '''Antwort:''' Die Funktionsgleichung lautet | + | '''Antwort:''' Die Funktionsgleichung lautet $s(t)=2.75 \cdot t^2$. |
| + | '''c)''' $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia). | ||
| − | |||
Berechnen Sie: | Berechnen Sie: | ||
| Zeile 106: | Zeile 97: | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> s(t) ist die Formel der zurückgelegten Strecke | + | <div class="mw-collapsible-content"> $s(t)$ ist die Formel der zurückgelegten Strecke. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wo sich die Rakete nach $180$ Sekunden befindet. |
</div> | </div> | ||
</div> | </div> | ||
| Zeile 112: | Zeile 103: | ||
| − | $$s(t)=2 | + | $$s(t)=2.75 \cdot t^2$$ |
| − | $$s(180)=2 | + | $$s(180)=2.75 \cdot 180^2$$ |
| − | $$s(180)= | + | $$s(180)=89 100 m$$ |
| − | '''Nach 180 Sekunden befindet sich unsere Rakete in einer Höhe von | + | '''Nach $180$ Sekunden befindet sich unsere Rakete in einer Höhe von $89 100 m$.''' |
| Zeile 125: | Zeile 116: | ||
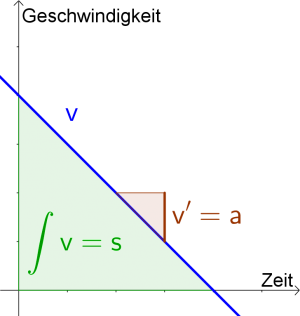
| − | + | [[Datei:C.png|miniatur|Das $k$ der Tangente gibt die Geschwindigkeit an.]] | |
| − | [[Datei:C.png|miniatur|Das k der Tangente gibt die Geschwindigkeit an]] | + | |
- die Geschwindigkeit der Rakete zu diesem Zeitpunkt. | - die Geschwindigkeit der Rakete zu diesem Zeitpunkt. | ||
| Zeile 133: | Zeile 123: | ||
{{Vorlage:Ausklapp|1= Tipp zur Berechnung: | {{Vorlage:Ausklapp|1= Tipp zur Berechnung: | ||
|2= | |2= | ||
| − | v(t) ist die Formel, die die Geschwindigkeit zum Zeitpunkt t angibt | + | $v(t)$ ist die Formel, die die Geschwindigkeit zum Zeitpunkt $t$ angibt. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wie hoch die Geschwindigkeit der Rakete nach $180$ Sekunden ist. Das Ergebnis erscheint in $m/s$. Wenn das Ergebnis in $km/h$ gewünscht wäre, müsste man das Ergebnis noch $\cdot 3.6$ rechnen. |
}} | }} | ||
| − | + | $$v(t)=5.5 \cdot t$$ | |
| − | $$v(t)=5 | + | $$v(180)=5.5 \cdot 180$$ |
| − | $$v(180)=5 | + | |
$$v(180)=990 m/s$$ | $$v(180)=990 m/s$$ | ||
<br /> | <br /> | ||
| − | $$990 m/s \rightarrow | + | $$990 m/s \rightarrow 3 564 km/h$$ |
| − | '''Nach 180 Sekunden hat unsere Rakete eine Geschwindigkeit von | + | '''Nach $180$ Sekunden hat unsere Rakete eine Geschwindigkeit von $3 564 km/h$ erreicht.''' |
| − | '''d)''' In etwa 1000 km Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. | + | '''d)''' In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird. |
| Zeile 157: | Zeile 146: | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Die Funktion s beschreibt den zurückgelegten Weg. Wenn wir die unrealistische Annahme voraussetzen, dass die Rakete | + | <div class="mw-collapsible-content"> Die Funktion $s$ beschreibt den zurückgelegten Weg. Wenn wir die unrealistische Annahme voraussetzen, dass die Rakete „kerzengerade“ emporsteigt, müssen wir somit berechnen, wann $s(t)=1000 km=1 000 000 m$ beträgt. |
| − | Wichtig ist hierbei, dass s(t) den Weg in m | + | Wichtig ist hierbei, dass $s(t)$ den Weg in $m$ angibt! </div> |
</div> | </div> | ||
| − | $$1 | + | $$1 000 000=2.75 \cdot t^2$$ |
| − | $$t=603 | + | $$t=603.02$$ |
<br /> | <br /> | ||
| − | '''Nach 603 | + | '''Nach $603.02$ Sekunden erreichen wir mit unserer Rakete die Höhe $1 000 000$ Meter.''' |
}} | }} | ||
| − | |||
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 181: | Zeile 168: | ||
| − | Ein Raumschiff hat eine Beschleunigung von 7 | + | Ein Raumschiff hat eine Beschleunigung von $7.94 m/s^2$. Gehen Sie im Folgenden davon aus, dass die Beschleunigung während der ganzen Fahrt konstant bleibt, d. h. $a(t)=7.94 m/s^2$. |
| − | Gehen Sie im Folgenden davon aus, dass die Beschleunigung während der ganzen Fahrt konstant bleibt | + | Die Variable $t$ gibt die Zeit nach dem Start in Sekunden an. |
| − | Die | + | |
| − | + | '''a)''' Bestimmen Sie die Funktion $v(t)$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angibt. (Anfangsfunktion $= 0$) | |
| − | + | ||
| − | '''a)''' Bestimmen Sie die Funktion v(t), die die Geschwindigkeit der Rakete nach t Sekunden angibt. (Anfangsfunktion = 0) | + | |
| Zeile 194: | Zeile 178: | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Da die Funktion der Geschwindigkeit v(t) gesucht wird, müssen wir die Formel der Beschleunigung a(t) einmal integrieren. Wir setzen 7 | + | <div class="mw-collapsible-content"> Da die Funktion der Geschwindigkeit $v(t)$ gesucht wird, müssen wir die Formel der Beschleunigung $a(t)$ einmal integrieren. Wir setzen $7.94$ (dies entnehmen wir aus der Angabe) für $a(t)$ ein und berechnen so unser Ergebnis für $v(t)$. Außerdem ist anzumerken, dass $c$ wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ beträgt und dadurch $c$ nach dem integrieren wegfällt. |
</div> | </div> | ||
</div> | </div> | ||
| − | |||
$$v(t)=\int a(t) \cdot dt$$ | $$v(t)=\int a(t) \cdot dt$$ | ||
| − | $$v(t)=\int 7 | + | $$v(t)=\int 7.94 \cdot dt$$ |
| − | $$v(t)=7 | + | $$v(t)=7.94 \cdot t (+ c)$$ |
| − | $$v(t)=7 | + | $$v(t)=7.94 \cdot t$$ |
| − | '''Die Funktion lautet | + | '''Die Funktion lautet $$v(t)=7.94 \cdot t$$.''' |
| − | + | '''b)''' Bestimmen Sie mithilfe der Geschwindigkeitsfunktion $v(t)$ die Funktion $s(t)$, die den nach $t$ Sekunden zurückgelegten Weg angibt. | |
| − | + | ||
| − | '''b)''' Bestimmen Sie mithilfe | + | |
| Zeile 218: | Zeile 199: | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Da die Funktion des Weges s(t) gesucht wird, müssen wir die Formel der Geschwindigkeit v(t) einmal integrieren. Wir setzen 7 | + | <div class="mw-collapsible-content"> Da die Funktion des Weges $s(t)$ gesucht wird, müssen wir die Formel der Geschwindigkeit $v(t)$ einmal integrieren. Wir setzen $7.94$ (dies entnehmen wir aus dem Ergebnis, der oberen Aufgabe) für $v(t)$ ein und berechnen so unser Ergebnis für $s(t)$. Außerdem ist anzumerken, dass $c$ wieder wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ beträgt und dadurch $c$ nach dem Integrieren wegfällt. |
</div> | </div> | ||
</div> | </div> | ||
| Zeile 224: | Zeile 205: | ||
| − | $$v(t)= 7 | + | $$v(t)= 7.94 \cdot t (+c)$$ |
| − | $$s(t)=\int 7 | + | $$s(t)=\int 7.94 \cdot dt$$ |
| − | $$s(t)=\int 7 | + | $$s(t)=\int 7.94 \cdot dt (+ c)$$ |
| − | $$s(t)=7 | + | $$s(t)=7.94 (t^2)/2 + c \cdot t$$ |
| − | $$s(t)=3 | + | $$s(t)=3.97 \cdot t^2 (+ c \cdot t)$$ |
| − | '''Die Funktion lautet: $$s(t)=3 | + | '''Die Funktion lautet: $$s(t)=3.97 \cdot t^2 (+ c \cdot t)$$ |
''' | ''' | ||
| − | |||
| − | |||
| Zeile 241: | Zeile 220: | ||
| − | - die zurückgelegte Distanz nach 300 Sekunden | + | - die zurückgelegte Distanz nach $300$ Sekunden. |
| Zeile 247: | Zeile 226: | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Da wir ermitteln wollen, wie viele Meter wir nach 300 Sekunden zurückgelegt haben, verwenden wir die Funktion des Weges s(t). Für unsere Zeit setzen wir 300 Sekunden ein. Außerdem ist anzumerken, dass | + | <div class="mw-collapsible-content"> Da wir ermitteln wollen, wie viele Meter wir nach $300$ Sekunden zurückgelegt haben, verwenden wir die Funktion des Weges $s(t)$. Für unsere Zeit setzen wir $300$ Sekunden ein. Außerdem ist anzumerken, dass $c$ wieder wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ ist. |
</div> | </div> | ||
</div> | </div> | ||
| Zeile 253: | Zeile 232: | ||
| − | $$s(300)= 3 | + | $$s(300)= 3.9t \cdot 300^2 (+c \cdot t)$$ |
| − | $$s(300)= | + | $$s(300)= 357 300 m$$ |
| − | - die Geschwindigkeit zu diesem Zeitpunkt | + | - die Geschwindigkeit zu diesem Zeitpunkt. |
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Da wir ermitteln wollen, wie hoch die Geschwindigkeit nach 300 Sekunden ist, verwenden wir die Funktion der Geschwindigkeit v(t). Für unsere Zeit setzen wir daher 300 Sekunden ein. Außerdem ist anzumerken, dass | + | <div class="mw-collapsible-content"> Da wir ermitteln wollen, wie hoch die Geschwindigkeit nach $300$ Sekunden ist, verwenden wir die Funktion der Geschwindigkeit $v(t)$. Für unsere Zeit setzen wir daher $300$ Sekunden ein. Außerdem ist anzumerken, dass $c$ wieder wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ ist. |
</div> | </div> | ||
</div> | </div> | ||
| Zeile 269: | Zeile 248: | ||
| − | $$v(300)= 7 | + | $$v(300)= 7.94 \cdot 300 (+c)$$ |
| − | $$v(300)= | + | $$v(300)= 2 382 m/s$$ |
| − | + | $2 382 m/s \rightarrow 661.67 km/h$ | |
| − | '''d)''' Nach | + | '''d)''' Nach $2 000 km$ erreicht das Raumschiff den Mars. Ermitteln Sie, nach wie vielen Sekunden das Raumschiff den Mars erreicht. |
| Zeile 284: | Zeile 263: | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
<span style="color:#A020F0> Tipp zur Berechnung: </span> | <span style="color:#A020F0> Tipp zur Berechnung: </span> | ||
| − | <div class="mw-collapsible-content"> Da wir ermitteln wollen, nach wie vielen Sekunden das Raumschiff den Mars erreicht, verwenden wir die Funktion des Weges s(t). Für unseren Weg setzen wir daher | + | <div class="mw-collapsible-content"> Da wir ermitteln wollen, nach wie vielen Sekunden das Raumschiff den Mars erreicht, verwenden wir die Funktion des Weges $s(t)$. Für unseren Weg setzen wir daher $2 000 m$ ein (Wir rechnen zuvor noch $km$ in $m$ um, da wir die Zeit in Sekunden angegeben haben wollen.). |
</div> | </div> | ||
</div> | </div> | ||
| − | $$2 | + | $$2 000 000=3.97 \cdot t^2$$ |
| − | $$t = 709 | + | $$t = 709.77 Sek.$$ |
| − | 709 | + | $709.77 s \rightarrow 11.83 min$ |
<br /> | <br /> | ||
| Zeile 304: | Zeile 283: | ||
[http://www.brinkmann-du.de/physik/ph_aufgaben/phob_a02/phob_a02.htm Beispiele samt Lösungen von brinkmann-du] | [http://www.brinkmann-du.de/physik/ph_aufgaben/phob_a02/phob_a02.htm Beispiele samt Lösungen von brinkmann-du] | ||
| − | |||
| − | |||
== Quiz == | == Quiz == | ||
Version vom 28. Dezember 2018, 16:40 Uhr
Inhaltsverzeichnis
Begriffe
Wird die Geschwindigkeit $v$ durch den Graphen angegeben, so ist die Steigung die Beschleunigung $a$. Der Flächeninhalt unter $v$ gibt den Weg $s$ an.
- $s(t)$ gibt den zurückgelegten Weg zum Zeitpunkt $t$ an (Einheit: $m$ oder $km$ ...)
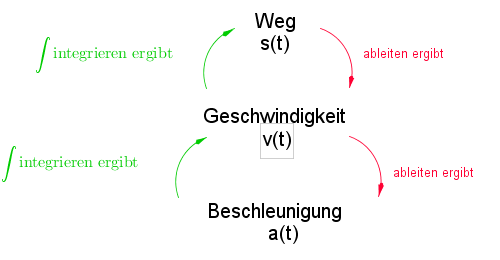
- $v(t)$ gibt die Momentangeschwindigkeit zum Zeitpunkt $t$ an (Einheit: $m/s$ oder $km/h$ ...). Die Geschwindigkeit ist die momentane Änderung des Weges $s(t)$, d. h.
$$s'(t)=v(t)\textrm{ bzw. } \int v(t)=s(t)+c,\textrm{ wobei $c$ die Anfangsstrecke $s_0$ angibt.}$$
- $a(t)$ gibt die Beschleunigung zum Zeitpunkt $t$ an (Einheit: $m/s^2$ oder $km/h^2$ ...). Die Beschleunigung ist die momentane Änderung der Geschwindigkeit $v(t)$, d. h.
$$v'(t)=a(t)\textrm{ bzw. } \int a(t)=v(t)+c,\textrm{ wobei $c$ die Anfangsgeschwindigkeit $v_0$ angibt.}$$
Vereinfacht gesagt gilt folgender Zusammenhang:
Beispiele
Die ESA (European Space Agency) bringt mithilfe der Ariane 5 regelmäßig Satelliten in den Weltraum. Die Startbeschleunigung beträgt dabei ca. $5.5 m/s^2$. Gehen Sie im Folgenden davon aus, dass die Beschleunigung während des ganzen Fluges konstant ist (d. h. $a(t)=5.5 m/s^2$). Die Variable $t$ gebe die Zeit nach dem Start in Sekunden ($s$) an.
a)Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$)
b) Bestimmen Sie mithilfe von $v$ die Funktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt.
c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia).
Berechnen Sie:
- die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet.
- die Geschwindigkeit der Rakete zu diesem Zeitpunkt.
d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird.
a)Bestimmen Sie die Funktion $v$, die die Geschwindigkeit der Rakete nach $t$ Sekunden angebe. (Hinweis für die Integrationskonstante: Die Anfangsgeschwindigkeit $v(0)=v_0=0$)
Tipp zur Berechnung:
Da die Funktion der Geschwindigkeit $v(t)$ gesucht wird, müssen wir die Formel der Beschleunigung $a(t)$ einmal integrieren. Wir setzen $5.5$ (Dies entnehmen wir aus der Angabe) für $a(t)$ ein und berechnen $v(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=v_0$ wegfällt, da unsere Anfangsgeschwindigkeit (Geschwindigkeit zum Zeitpunkt $t=0$) $0$ beträgt und damit $v(0)=0$ gelten muss.
$$v(t)=\int a(t) \cdot dt$$
$$v(t)=\int 5.5 \cdot dt$$
$$v(t)=5.5 \cdot t + v_0$$
$$v(t)=5.5 \cdot t$$
Antwort: Die Geschwindigkeitsfunktion lautet $v(t)=5.5 \cdot t$.
b) Bestimmen Sie mithilfe von $v$ die Wegfunktion $s$, die den nach $t$ Sekunden zurückgelegten Weg angibt.
Tipp zur Berechnung:
Da die Funktion des Weges $s$ gesucht wird, müssen wir die Formel der Geschwindigkeit $v(t)$ einmal integrieren. Wir setzen $5.5t$ (dies entnehmen wir aus dem Ergebnis von Aufgabe a) für $v(t)$ ein und berechnen so unser Ergebnis für $s(t)$. Außerdem ist anzumerken, dass die Integrationskonstante $c=s_0$ wegfällt, da unsere zurückgelegte Strecke zu Beginn $0$ ist.
$$s(t)=\int v(t) \cdot dt$$
$$s(t)=\int 5.5t \cdot dt$$
$$s(t)=5.5 \cdot \frac{t^2}{2} +c$$
$$s(t)=2.75 \cdot t^2$$
Antwort: Die Funktionsgleichung lautet $s(t)=2.75 \cdot t^2$.
c) $180$ Sekunden nach dem Start sind die Feststoffbooster ausgebrannt und werden abgesprengt (Quelle: Wikipedia).
Berechnen Sie:
- die Höhe, in der sich die Rakete zu diesem Zeitpunkt befindet.
Tipp zur Berechnung:
$s(t)$ ist die Formel der zurückgelegten Strecke. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wo sich die Rakete nach $180$ Sekunden befindet.
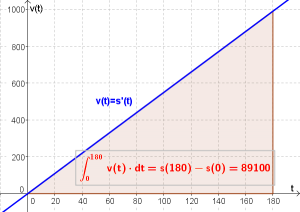
$$s(t)=2.75 \cdot t^2$$ $$s(180)=2.75 \cdot 180^2$$ $$s(180)=89 100 m$$
Nach $180$ Sekunden befindet sich unsere Rakete in einer Höhe von $89 100 m$.
.png)
- die Geschwindigkeit der Rakete zu diesem Zeitpunkt.
Tipp zur Berechnung:
$v(t)$ ist die Formel, die die Geschwindigkeit zum Zeitpunkt $t$ angibt. Wir setzen daher in diese Formel für die Zeit $t=180$ ein, da wir wissen wollen, wie hoch die Geschwindigkeit der Rakete nach $180$ Sekunden ist. Das Ergebnis erscheint in $m/s$. Wenn das Ergebnis in $km/h$ gewünscht wäre, müsste man das Ergebnis noch $\cdot 3.6$ rechnen.
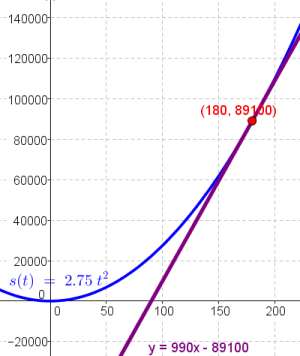
$$v(t)=5.5 \cdot t$$
$$v(180)=5.5 \cdot 180$$
$$v(180)=990 m/s$$
$$990 m/s \rightarrow 3 564 km/h$$
Nach $180$ Sekunden hat unsere Rakete eine Geschwindigkeit von $3 564 km/h$ erreicht.
d) In etwa $1000 km$ Höhe erreicht die Rakete die geostationäre Umlaufbahn (Quelle: Wikipedia). Ermitteln Sie, nach wie vielen Sekunden diese Umlaufbahn erreicht wird.
Tipp zur Berechnung:
Die Funktion $s$ beschreibt den zurückgelegten Weg. Wenn wir die unrealistische Annahme voraussetzen, dass die Rakete „kerzengerade“ emporsteigt, müssen wir somit berechnen, wann $s(t)=1000 km=1 000 000 m$ beträgt.
Wichtig ist hierbei, dass $s(t)$ den Weg in $m$ angibt!
$$1 000 000=2.75 \cdot t^2$$
$$t=603.02$$
Nach $603.02$ Sekunden erreichen wir mit unserer Rakete die Höhe $1 000 000$ Meter.
Weitere Beispiele
Beispiele samt Lösungen von brinkmann-du
Quiz
noch zu überarbeiten!
