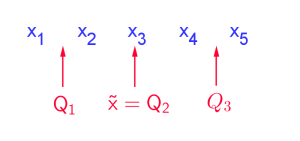Beschreibende Statistik
$Step\ by\ Step!$ Lernpfad beschreibende Statistik
In der beschreibenden Statistik beschäftigen wir uns mit der Auswertung von Datenmengen. Die Auswertung erfolgt dabei über graphische Darstellungsformen (Diagramme) und einzelne aussagekräftige Kennzahlen (z.B. Mittelwert, Spannweite, ...) mit denen Rückschlüsse auf Grundgesamtheit aller Daten bezogen werden können.
Inhaltsverzeichnis
Begriffe
$n...$ Umfang der Stichprobe
$x_1...$ Zahl an der 1. Stelle
$x_i...$ Zahl an der $i.$ Stelle
$\{ x_1;x_2;.....;x_n \} ...$ Stichprobe (z.B. $\{ 1; ;5; 5; 5; 10;\}$ )
$a_1...$ erster Wert, der in der Stichprobe vorkommt (im oberen Beispiel ist $a_1=1$)
$a_2...$ zweiter Wert, der in der Stichprobe vorkommt (im oberen Beispiel ist $a_2=5$)
$a_i...$ $i.$Wert, der in der Stichprobe vorkommt
Arten von Merkmalen/Daten
Im groben unterscheidet man zwischen 3 Arten von Merkmalen:
- nominale Merkmale können nicht sinnvoll durch eine Zahl beschrieben oder in eine Reihenfolge gebracht werden. Beispiele sind "Geschlecht", "Haarfarbe".
- ordinale Merkmale können in eine Reihenfolge gebracht werden, eignen sich aber nicht für Rechnungen (wie z.B. Addition). Beispiele sind "Platzierung bei einem Rennen", "Bildungsabschlüsse".
- metrische Merkmale können durch Zahlen beschrieben werden, mit denen man auch rechnen kann. Beispiele: "Gehalt", "Alter", "Schuhgröße".
Absolute und relative Häufigkeit
|
Die absolute Häufigkeit $H_i$ gibt an, wie oft das $i-$te Element in der Stichprobe auftritt.
z.B.: In der Menge $\{ 1;2;2;2;4;4;6\} $ ist die absolute Häufigkeit der Zahl 2 genau $H=3$, da die 2 insgesamt dreimal vorkommt |
In einer (kleinen) Umfrage werden von $n=15$ Personen die Schuhgrößen gemessen. Das Ergebnis ist in der folgenden Liste angegeben:
$$\{36;36;36;37;37;37;37;38;38;40;41;42;42;42;46\}$$
Aufgabe: Ermitteln Sie in einer Tabelle die Häufigkeit jedes Merkmals (=$a_i$).
{
| Werte $a_i$ | Häufigkeiten $H_i$ |
|---|---|
| 36 | 3 |
| 37 | 4 |
| 38 | 2 |
| 40 | 1 |
| 41 | 1 |
| 42 | 3 |
| 46 | 1 |
| Summe | 15 |
Aus der absoluten Häufigkeit kann man noch nicht darauf schließen, ob ein Merkmal wirklich häufig auftritt oder nicht, da es immer auch auf die Gesamtanzahl $n$ der untersuchten Werte ankommt.
So ist eine absolute Häufigkeit von $100$ für $n=150$ sehr groß, für $n=1$ Mrd dagegen wohl eher klein.
In solchen Fällen ist es hilfreich zu wissen, wie viel Prozent der Gesamtmenge $n$ dieses Merkmal besitzen. Dies wird berechnet mit...
|
Die relative Häufigkeit $h_i$ gibt an, mit wie viel Prozent ein Merkmal in Bezug auf die Gesamtmenge $n$ auftritt. Es gilt:
$$h_i=\frac{H_i}{n}$$ z.B.: In der Menge $\{1;2;2;2;4;4;6\}$ ist die absolute Häufigkeit der Zahl 2 genau $H=3$, die relative Häufigkeit ergibt sich dann mit: $$h=\frac{H}{n}=\frac{3}{7}\approx 43\%$$ |
Berechnen Sie mithilfe der Tabelle aus der Schuhgrößenumfrage (siehe oben) die relative Häufigkeiten $h_i$. {
| Werte $a_i$ | absolute Häufigkeiten $H_i$ | relative Häufigkeiten $h_i$ |
|---|---|---|
| 36 | 3 | $\ \ \ $ |
| 37 | 4 | |
| 38 | 2 | |
| 40 | 1 | |
| 41 | 1 | |
| 42 | 3 | |
| 46 | 1 | |
| Summe | 15 |
$n=15$ {
| Werte $a_i$ | absolute Häufigkeiten $H_i$ | relative Häufigkeiten $h_i$ |
|---|---|---|
| 36 | 3 | $\frac{3}{15}=20$% |
| 37 | 4 | $\frac{4}{15}=26.7$% |
| 38 | 2 | $\frac{2}{15}=13.3$% |
| 40 | 1 | $\frac{1}{15}=6.7$% |
| 41 | 1 | $\frac{1}{15}=6.7$% |
| 42 | 3 | $\frac{3}{15}=20$% |
| 46 | 1 | $\frac{1}{15}=6.7$% |
| Summe | 15 | $\frac{15}{15}=100$% |
Diagramme
Stab- und Balken-/Säulendiagramme
Kreisdiagramm
Boxplot (Kastenschaubild)
http://tube.geogebra.org/student/m5245
http://tube.geogebra.org/student/m274871 (Andi Lindner)
http://tube.geogebra.org/student/b115371#material/56673 (sollte bearbeitet werden)
http://tube.geogebra.org/student/m129201 (Test)
Schummeln mit Statistik
Rest folgt noch
Zentralmaße - statistische Kennzahlen für das Mittel
Um "das Mittel" zu berechnen, gibt es verschiedene Möglichkeiten. Dabei hat jede Vor- und Nachteile:
arithmetisches Mittel $\bar{x}$
Definition
Das arithmetische Mittel verwendest du in der Schule regelmäßig, um deine Durchschnittsnote zu berechnen. Dabei zählst du alle Noten zusammen und dividierst sie durch die Anzahl der Noten.
Z.B.: Gegeben ist die Menge an Schulnoten $\{ 1;2;2;2;5\} $. Das arithmetische Mittel (="Durchschnittsnote") ergibt: $$\rightarrow \bar{x}=\frac{1+2+2+2+5}{5}=\frac{12}{5}=2.4$$
|
Das arithmetische Mittel $\bar{x}$ ist definiert als
$$\bar{x}=\frac{x_1+x_2+...+x_n}{n}$$ $$(Summe\ aller\ Werte,\ dividiert\ durch\ die\ Anzahl)$$ Formal: $$\bar{x}=\frac{1}{n}\cdot \sum_{i=1}^{n} x_i$$ |
Das gewichtete arithmetische Mittel
Sind bereits die absoluten oder relativen Häufigkeiten für das arithmetische Mittel bekannt, so kann auch eine der folgenden Formeln für das "gewichtete arithmetische Mittel" verwendet werden:
|
Formel mit der absoluten Häufigkeit
$$\bar{x}=\frac{a_1\cdot H_1+a_2\cdot H_2+...}{n}=\frac{1}{n}\cdot \sum_{i} a_i\cdot H_i$$ $$(Summe\ aller\ Werte\ mal\ deren\ abs.\ Häufigkeit,\ dividiert\ durch\ n)$$ |
Beispiel zur Berechnung des arithmetischen Mittels mithilfe der absoluten Häufigkeiten:
Gegeben sind die Notenmenge $\{ 1;2;2;2;5\} $. Zuerst erstellen wir die Häufigkeitstabelle
| Noten $a_i$ | $H_i$ | $h_i$ |
|---|---|---|
| 1 | 1 | $\frac{1}{5}=20$% |
| 2 | 3 | $\frac{3}{5}=60$% |
| 5 | 1 | $\frac{1}{5}=20$% |
| $\sum$ | 5 | $\frac{5}{5}=100$% |
Setzen wir in die Formel für die absolute Häufigkeit ein, so erhalten wir
$$\bar{x}=\frac{a_1\cdot H_1+a_2\cdot H_2+a_3\cdot H_3}{n}$$
$$\bar{x}=\frac{1\cdot 1+2\cdot 3+5\cdot 1}{5}=\frac{12}{5}=2.4$$
|
Formel mit der relativen Häufigkeit
$$\bar{x}=a_1\cdot h_1+a_2\cdot h_2+...=\sum_{i} a_i\cdot h_i $$ $$(Summe\ aller\ Werte\ mal\ deren\ rel.\ Häufigkeit)$$
|
Beispiel zur Berechnung des arithmetischen Mittels mithilfe der relativen Häufigkeiten:
Gegeben sind die Noten=$\{ 1;2;2;2;5\} $. Um das arithmetische Mittel zu berechnen, lesen wir die Werte sowie die relativen Häufigkeiten aus der Häufigkeitstabelle und setzen in die Formel ein:
| Noten $a_i$ | $H_i$ | $h_i$ |
|---|---|---|
| 1 | 1 | $\frac{1}{5}=20$% |
| 2 | 3 | $\frac{3}{5}=60$% |
| 5 | 1 | $\frac{1}{5}=20$% |
| $\sum$ | 5 | $\frac{5}{5}=100$% |
$$\bar{x}=a_1\cdot h_1+a_2\cdot h_2+a_3\cdot h_3=1\cdot \frac{1}{5}+2\cdot \frac{3}{5}+5\cdot \frac{1}{5}$$
$$\bar{x}=\frac{12}{5}=2.4$$
|
|
Neben dem arithmetischen Mittel gibt es nun noch einen weiteren wichtigen Zentralwert, den...
Median $\tilde{x}$
|
Sortiert man eine Datenliste nach Größe, so ist der Median $\tilde{x}$ der Wert in der Mitte der geordneten Liste
Liegen genau zwei werte in der Mitte (was immer dann der Fall ist, wenn die Anzahl der Werte $n$ gerade ist), so ist $\tilde{x}$ das arithm. Mittel dieser beiden Werte.
Formal: $\begin{align} &\tilde{x}=x_{\frac{n+1}{2} }&& \textrm{ für ungerade n}\\ &\tilde{x}=\frac{1}{2}\cdot \left(x_{\frac{n}{2} }+ x_{\frac{n+1}{2} } \right)&& \textrm{ für gerade n}\\ \end{align}$ |
Beispiel für den Median: Geben ist die folgende Liste an Schulnoten $\{1;2;2;2;5\}$. Ermitteln sie den Median $\tilde{x}$.
Lösung: Insgesamt sind es $n=5$ Werte. Da die Liste bereits nach Größe geordnet ist, können wir den Median einfach ablesen:
| durch Ablesen | $\{1;2;\color{red}{2};2;5\}$ |
| rechnerisch | $$\tilde{x}=x_{\frac{5+1}{2}}=x_3=2$$ |
Der Median $\tilde{x}$ ist der Wert an der dritten Stelle und somit $\tilde{x}=2$
Vorteil des Median - Nachteil des arithmetischen Mittels
Vergleichen wir noch einmal das arithmetische Mittel und den Median unserer Notenliste $\{1;2;2;2;5\}$. $$\bar{x}=2.4 \textrm{ und } \tilde{x}=2$$ Warum ist das arithmetische Mittel größer, als der Median?
Antwort: Der Grund liegt daran, dass das arithmetische Mittel durch den "Ausreißer" 5 verzerrt wurde. Der Median hat sich dadurch nicht verändert.
|
Allgemein gilt:
Hinweis: Als Ausreißer gelten Zahlen, die im Vergleich zu den anderen Werten sehr klein oder sehr groß sind |
$Aha!$ Zur besseren Verdeutlichung kannst du dir dieses Arbeitsblatt ansehen (Klicke dabei zuerst auf "Median" und "Mittelwert" und verändere dann die Zahlen).
Aufgaben zum Arbeitsblatt
- Setze "Zahl der Datenwerte" auf 5.
- Schiebe nun 4 Werte auf "1" und einen auf "4". Wie verhält sich der Median, wie der Mittelwert?
- Verteile anschließend alle 5 Werte gleichmäßig auf den Zahlengeraden.
- Nimm dann den ganz linken Wert und verschiebe ihn langsam ganz nach rechts. Beobachte dabei, wann und wie sich Median und arithmetisches Mittel verändern.
Lösungen:
1. Der Median ist der mittlere Wert aller 5 Werte und bleibt deshalb bei 1. Mittelwert dagegen liegt zwischen 1 und 4.
2. Der Median bleibt gleich, solange der zu verschiebende Wert nicht in der MItte ist. Der Mittelwert ändert seinen Wert ständig.
Hinweis: Ein etwas komplexeres Arbeitsblatt findest du hier
Modus
kommt bald
geometrisches Mittel
statistische Kennzahlen für die Streuung
Im vorigen Kapitel haben wir gelernt, wie wir verschiedene Arten von Zentralmaßen bestimmen. Ein Zentralmaß allein sagt uns allerdings noch nicht viel über die Verteilung (=Streuung) der Werte aus.
Bilder von 2 Zahlensträngen mit denselben Zentralmaßen, aber unterschiedlichen Streuungen
Beide Datenmengen haben dieselben Zentralmaße, aber unterschiedliche Streuungen. Die Werte im linken Bild liegen näher um die Zentralmaße, als die Werte im rechten Bild.
Aus diesem Grund lernen wir nun noch zusätzlich Kennzahlen für die Streuung von Werten.
Spannweite
|
Die Spannweite ist die Differenz (Abstand) zwischen dem kleinsten und dem größten Wert der Datenmenge.
$$Spannweite=x_{max}-x_{min}$$ |
Beispiel: Gegeben sei die Datenmenge $\{1;2;2;2;5\}$. Bestimme die Spannweite.
Lösung: $x_{max}=5;\ x_{min}=1$ $$Spannweite=x_{max}-x_{min}=5-1=4$$
Die Spannweite beträgt $4$
Varianz und Standardabweichung
Eine andere Möglichkeit, um die Streuung anzugeben wäre foldende: Wir berechnen den durchschnittlichen Abstand aller Werte vom arithmetischen Mittel $\bar{x}$ zu berechnen. Diesen durchschnittlichen Abstand nennen wir Standardabweichung oder kurz $\sigma$ (=sigma).
Herleitung der Standardabweichung Um die durchschnittlichen Abstand aller Werte vom arithmetischen Mittel $\bar{x}$ (=Standardabweichung) zu erhalten machen wir folgendes:
- Schritt: Wir berechnen den Abstand aller Werte von $\bar{x}$:
- $$(x_1-\bar{x}) \textrm{ und } (x_2-\bar{x}) \textrm{ und ... und } (x_n-\bar{x})$$
- Schritt: Da die Abstände mitunter negativ sind (wenn $x_i<\bar{x}$), quadrieren wir alle Abstände:
- $$(x_1-\bar{x})^2 \textrm{ und } (x_2-\bar{x})^2 \textrm{ und ... und } (x_n-\bar{x})^2$$
- Schritt: Nun zählen wir die quadrate aller Abstände zusammen und berechnen den Durchschnitt (d.h. wir dividieren durch $n$:
- $$\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n}$$
- Da wir oben quadriert haben, ziehen wir nun wieder die Wurzel (Achtung! Dadurch fallen die $(\ )^2$ nicht weg!):
- $$\sqrt{\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n} }$$
Oder verkürz angeschrieben: $$\sqrt{ \frac{\sum_{i}(x_i-\bar{x})^2}{n} }$$
|
Die Standardabweichung $\sigma$ gibt die Streuung aller Werte vom Erwartungswert $\bar{x}$ an und wird berechnet mit
$$\sigma=\sqrt{\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n} }$$ Verkürzt: $$\sigma=\sqrt{ \frac{\sum_{i}(x_i-\bar{x})^2}{n} }$$
|
Berechnen Sie arithmetisches Mittel und Standardabweichung der Liste $\{1;2;2;2;5\}$.
$$\bar{x}=\frac{1+2\cdot 3+5}{5}=\frac{12}{5}=2.4$$ Somit beträgt das arithm. Mittel $\bar{x}=2.4$
Um die Standardabweichung zu berechnen, ermitteln wir zuerst die Varianz und ziehen anschließend die Wurzel (so vermeiden wir häufige Rechenfehler):
$$\sigma^2 =\frac{(x_1-\bar{x})^2 + (x_2-\bar{x})^2 +...+ (x_n-\bar{x})^2}{n}$$
$$\sigma^2=\frac{(1-2.4)^2+(1-2.4)^2+(2-2.4)^2+(2-2.4)^2+(2-2.4)^2+(5-2.4)^2}{5}$$
$$\sigma^2=\frac{(1-2.4)^2+(2-2.4)^2\cdot 3+(5-2.4)^2}{5}$$
$$\sigma^2=\frac{(-1.4)^2+(-0.4)^2\cdot 3+2.6^2}{5}$$
$$\sigma^2=\frac{9.2}{5}=1.84$$
Somit erhalten wir für die Standardabweichung $\sigma$:
$$\sigma=\sqrt{\sigma^2}=\sqrt{1.84}=1.36$$
Die Standardabweichung beträgt $\sigma=1.36$
Quartile
|
Die Quartile $Q_1,\ Q_2\ (=\tilde{x}),\ Q_3$ teilen die Werte der Datenmenge insgesamt in 4 Bereiche.
Berechnung:
|
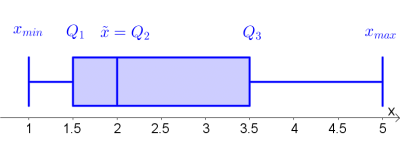
Die Quartile sind vor allem für die Erstellung eines Boxplot-Diagramms relevant.
Gegeben ist die Datenmenge $\{1;2;2;2;5\}$. Bestimme $x_{min},\ x_{max}$ sowie alle Quartile und erstelle damit ein Boxplotdiagramm.
|
Der Quartilsabstand" ist der Abstand zwischen den Quartilen $Q_1$ und $Q_3$.
$$Quartilsabstand=Q_3-Q_1$$ Graphsich entspricht dies der Länge der "Box" im Boxplot-Diagramm. |
Berechnung der Kennzahlen mit Technologie
GeoGebra
Ti-8x
Excel
Regression
$\rightarrow$ siehe Regression
Matura-Aufgaben
- $Bifie$ : Schiunfälle (bifie-Aufgabe: leicht)
- siehe auch Wachstums- und Zerfallsprozesse
- $Bifie$ : Radausflug (bifie-Aufgabe:mittel-mittel-mittel-leicht)
- Siehe auch
- * Wachstums- und Zerfallsprozesse
- * Trigonometrie