Inhalt:Integration:Das unbestimmte Integral - Berechnung der Stammfunktion

Inhalt:Integration:Das unbestimmte Integral - Berechnung der Stammfunktion

Für fast jede uns bekannte Rechenoperation existiert auch eine Umkehroperation (siehe Äquivalenzumformungen). Die Umkehroperation der Addition ist zum Beispiel die Subtraktion.

Die passende Umkehroperation zum Differenzieren (Ableitungen bestimmen) ist die Integration.

Wir haben bereits gelernt, dass wir zu einer Funktion $f$ die Ableitungsfunktion $f'$ bestimmen können mithilfe der Ableitungsregeln. Nun sollte es natürlich möglich sein, zu einer Ableitungsfunktion die dazugehörige Ausgangsfunktion zu finden. Man kann jede Funktion als Ableitung betrachten und demnach muss es zu jeder Funktion (die man selbst ableiten kann) auch eine Funktion geben, aus der sie durch Ableiten hervorgegangen ist. Diese Überlegung führt uns zum Begriff Stammfunktion.

Definition

Stammfunktion Die Funktion $F$ heißt Stammfunktion der Funktion $f$, wenn gilt: $$F'(x)=f(x)$$ Eine andere Schreibweise, die wir erst später rechtfertigen, ist: $$F(x)=\int f(x)\cdot dx$$

Musterbeispiel

$f(x)=2x$

$\rightarrow$

$F_1(x)=x^2$ $F_2(x)=x^2+3$ $F_3(x)=x^2-7.2$

weil $F_1'(x)=2x$ weil $F_2'(x)=2x$ weil $F_3'(x)=2x$

Alle diese Funktionen $F_1,\ F_2$ und $F_3$ sind Stammfunktionen von $f(x)=2x$, da die konstanten Zahlen durch das Ableiten wegfallen. Aus diesem Grund geben wir eine allgemeine Stammfunktion an:

Allgemeine Stammfunktion

$f(x)=2x \ \ \ \rightarrow \ \ \ F(x)=x^2+c$ mit $c\in$ $\mathbb{R}$.

weil $F'(x)=f(x) \leftrightarrow (x^2+c)'=2x$

Merke

Integrationskonstante $c$ Die Integrationskonstante $c$ ist jener unbekannte konstante Term ($c\in$ $\mathbb{R}$) der Stammfunktion, der durch das Ableiten wieder wegfällt. Wir sehen also, dass die Integration keine exakte Umkehrung des Differenzierens ist, da wir die Integrationskonstante $c$ ohne weitere Informationen nicht wieder zurückgewinnen können.

Beispiele

$f(x)=5$

$F(x)=5x+c$ weil $F'(x)=5$

$f(x)=3x^2$

$F(x)=x^3+c$ weil $F'(x)=3x^2$

$f(x)=x^2$

$F(x)=\frac{x^3}{3}+c$ weil $F'(x)=\frac{3\cdot x^2}{3}=x^2$

$f(x)=5x+2$

$F(x)=\frac{5x^2}{2}+2x+c$ weil $F'(x)=5x+2$

Integrationsregeln

	Regel	Bemerkung
Potenzregel	$$\int x^n\,dx=\frac{x^{n+1}}{n+1}+c$$	Exponent um $1$ erhöhen und mit dem neuen Exponenten dividieren. Die Potenzregel gilt für alle Potenzen mit $n\neq -1$
Summenregel	$$\int [f(x)± g(x)]\,dx=\int f (x)\,dx±\int g (x)\,dx$$	Eine Summe wird integriert, indem man jeden Summanden einzeln integriert.
Faktorregel	$$\int c\cdot f (x)\,dx=c\cdot\int f (x)\,dx$$	Einen konstanten Faktor kann man herausheben. Dies gilt auch für Brüche.
Regel für $\frac{1}{x}$	$$\int \frac{1}{x}\,dx=In|x|+c$$	Wobei $ln(x)$ der Logarithmus zur Basis $e$ ist. Diese Regel braucht man für $\frac{1}{x}=x^{-1}$
Regel für die Exponentialfunktion $e^x$	$$\int e^x=e^x+c$$	Wie beim Ableiten ändert sich auch beim Integrieren nichts.
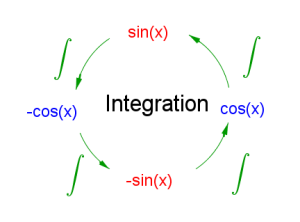
Trigonometrische Funktionen	$$\int sin(x)\cdot dx=-cos(x)+c$$ $$\int cos(x)\cdot dx=sin(x)+c$$	Integrationsregeln für die Sinus- und Cosinusfunktion

Beispiele

Bestimmen Sie alle Stammfunktionen:

$f(x)=3.7$

$F(x)=\int 3.7\cdot dx=3.7x+c$

$f(x)=2x+3$

$\int (2x+3)\cdot dx=x^2+3x+c$

$f(x)=-x+\frac{1}{2}$

$\int\left(-x+\frac{1}{2}\right)\cdot dx=-\frac{x^2}{2}+\frac{1}{2}x+c\ \ \ \ \ \ \ \ (\textrm{oder: }-0.5x^2+0.5x+c)$

$f(x)=\frac{x^2}{2}$

$\int \left( \frac{x^2}{2}\right) \cdot dx=\frac{x^3}{3\cdot 2}+c=\frac{x^3}{6}+c$

$f(x)=9x^2-8x+7$

$\int (9x^2-8x+7)\cdot dx=3x^3-4x^2+7x+c$

$f(x)=\frac{1}{x}$

$\int \frac{1}{x}\cdot dx=In\vert x\vert +c$

$f(x)=\frac{1}{x^2}+x^{-3}-\frac{5}{3}$

$\int x^{-2}+x^{-3}-\frac{5}{3}\cdot dx=\frac{x^{-1} }{-1}+\frac{x^{-2} }{-2}-\frac{5}{3}\cdot x +c=-\frac{1}{x}-\frac{1}{2x^2}+\frac{5}{3}\cdot x+c$

Zusatzmaterial

Die folgenden Materialien wurden von Schüler*innen der HLW Marienberg erstellt:

? $\ $ Kreuzworträtsel zum unbestimmten Integral

? $\ $ Zuordnungsaufgaben zu den Integrationsregeln