Differenzieren:Graphisches Bestimmen von f'

Die Ableitungsfunktion $f'(x)$ kann allein durch Betrachtung der ursprünglichen Funktion $f(x)$ graphisch bestimmt werden.

Das folgende Applet zeigt dir den Zusammenhang zwischen einer Funktion und ihrer Ableitungsfunktion. Verschiebe dazu den Punkt $P$ in der linken Graphik:

Aufgaben zu diesem Applet

Betrachte die linke Graphik: Der Wert $k$ zeigt die Steigung der Tangente im Punkt $P$ an.

1. Verschieben Sie den Punkt $P$. Auf der rechten Graphik wird laufend die Steigung $k$ beim jeweiligen $x$-Wert von $P$ abgetragen. Verschieben Sie $P$ solange, bis in der rechten Graphik ein schöner Funktionsgraph zu sehen ist. Dieser Graph ist der Graph von $f'(x)$ (=1. Ableitung von $x$).

2. Geben Sie eine andere Funktion im Eingabefeld ein. Versuchen Sie den Graphen von $f'(x)$ zuerst zu erraten und zeichnen Sie ihn erst dann durch Verschieben des Punktes $P$.

Funktionen zum Eintippen:
a) $f(x)=1.5x^3-4x^2$
b) $f(x)=0.05x^4-0.225x^3-0.325x^2+0.9x+0.5$
c) $f(x)=3x$

Merke

$f'(x)$ gibt die Steigung von $f(x)$ an. Somit muss gelten:

$f(x)$	$f'(x)$
1. $f(x)$ hat bei $a$ eine Extremstelle	$\rightarrow$ Hier ist die Steigung $f'(a)=0$
2. $f(x)$ hat bei $b$ einen Wendepunkt	$\rightarrow$ Hier ist der Graph lokal am steilsten oder am flachsten $\rightarrow$ die Steigung $f'$ hat hier einen Hoch- oder Tiefpunkt $\rightarrow$ $f''(b)=0$
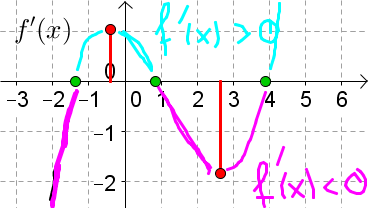
3. $f(x)$ ist monoton wachsend	$\rightarrow$ $f'(x)$ ist positiv, d. h. oberhalb der $x$-Achse.
4. $f(x)$ ist monoton fallend	$\rightarrow$ $f'(x)$ ist negativ, d. h. unterhalb der $x$-Achse.

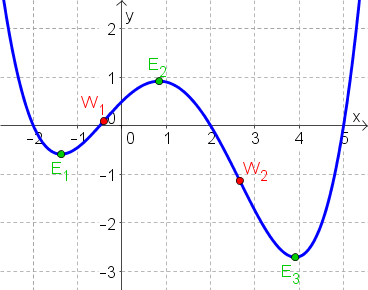
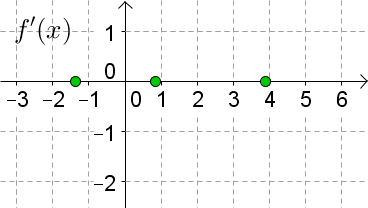
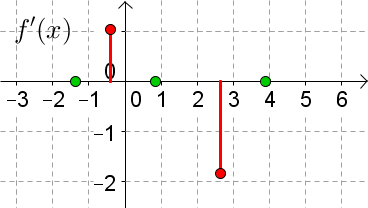
Skizzieren Sie zum gegebenen Graphen von $f(x)$ den Graphen von $f'(x)$.

Graph von f(x)

1. Schritt: Zeichne die Nullstellen von $f'(x)$ (= Extremwerte von $f(x)$) ein.	2. Schritt: Zeichne die Extremwerte von $f'(x)$ (= Wendepunkte von $f(x)$ ein. Die Höhen entsprechen den Steigungen von $f(x)$ bei den Wendepunkten.
3. und 4. Schritt: Aufgrund des Monotonieverhaltens von $f(x)$ wissen wir, wann $f'(x)$ positiv oder negativ ist.	$f'(x)$ schön eingezeichnet