Differenzengleichungen
- Einleitung
- Lineare Differenzengleichung (arithmetische Folge)
- Exponentielle Differenzengleichung (geometrische Folge)
- Interaktive Übungen
Einleitung
Differenzengleichungen ermöglichen es, praktische Fragestellungen aus der Finanzmathematik (Zinseszins-, Renten- und Tilgungsrechnung), der Populationsdynamik (Entwicklung einer Population) sowie aus vielen weiteren wissenschaftlichen Disziplinen der Wirtschaft, Medizin, Technik usw. mathematisch zu beschreiben.
Bei einer Differenzengleichung (auch Rekursionsgleichung genannt) handelt es sich um eine rekursive Folge, also um eine Aufzählung von Zahlen. Besteht eine Folge aus den Zahlen $x_0, x_1, x_2, x_3, …$ , so heißen diese Zahlen „Glieder der Folge“, wobei $x_0$ das 0. Folgeglied (= Anfangswert), $x_1$ das 1. Folgeglied usw. bezeichnet.
Rekursiv bedeutet, dass man unter Kenntnis eines Folgeglieds immer das nächste Folgeglied ermitteln kann.
Es gelte $y_0=4$ und $y_{n+1}=y_n-2$.
Ermitteln Sie $y_n$ für $n=1, 2, 3$.
$y_0$ … Anfangs- bzw. Startwert (erste Zahl der Zahlenfolge)
$\hspace{2.1cm} y_n$ … Wert nach $n$ Einheiten ($n$-tes Folgeglied)
$\hspace{2.1cm} y_{n+1}$ … Wert nach $(n+1)$ Einheiten ($(n+1)$-tes Folgeglied bzw. Nachfolger von $y_n$)
Anmerkungen: Anstelle der Schreibweise $y_0, y_n$ bzw. $y_{n+1}$ wird auch häufig die Form $y(0), y(n)$ bzw. $y(n+1)$ verwendet. Beachte, dass $n$ immer nur eine natürliche Zahl sein kann (d. h. $n=0, 1, 2, 3, …$). Denn es macht keinen Sinn das $-1$-te Folgeglied oder etwa das $1.5$-te Folgeglied zu berechnen.
Der Anfangswert der Zahlenfolge ist $4$. Jedes weitere Folgeglied ist um $2$ kleiner als das vorige. Somit erhalten wir $y_1$, indem wir vom Anfangswert $2$ abziehen. Es gilt:
$\boldsymbol{y_1}=y_0-2 \Rightarrow y_1=4-2=\boldsymbol{2}$
Das 2. Folgeglied $y_2$ erhalten wir nun, indem wir vom aktuellen Folgeglied $y_1$ erneut $2$ abziehen.
$\boldsymbol{y_2}=y_1-2\Rightarrow y_2=2-2=\boldsymbol{0}$
Analog resultiert für das 3. Folgeglied $\boldsymbol{y_3=-2}$.
Verständnisfrage: Warum wird durch die alleinige Angabe von $y_{n+1}=y_n-2$ für alle $n\in \mathbb{N}$ keine Folge eindeutig definiert?
Es fehlt die Anfangsbedingung, denn je nach Wahl des Anfangswertes ergibt sich eine andere Zahlenfolge. So erhalten wir für $y_0=3$ die Folge $(3, 1, -1, -3, …)$, für $y=4$ ergibt sich allerdings die Folge $(4, 2, 0, -2, …)$. Beide erfüllen die Bedingung $y_{n+1}=y_n-2$ für alle $n\in \mathbb{N}$, sind aber voneinander verschieden.
Es ist also unbedingt erforderlich, die Anfangsbedingung immer mit anzugeben!
Grundsätzlich unterscheidet man bei Differenzengleichungen zwei Grundformen:
- Lineare Differenzengleichung (arithmetische Folge)
- Exponentielle Differenzengleichung (geometrische Folge)
Lineare Differenzengleichung (arithmetische Folge)
Für ein lineares Wachstum ist eine konstante Zunahme in gleichen Zeitspannen charakteristisch.
Bei einer linearen Differenzengleichung wächst bzw. sinkt der angegebene Wert mit jedem Folgeglied um einen festen Betrag. Ein Beispiel dafür ist die einleitende Folge $y_{n+1}=y_n-2$, wo der Wert stets um $2$ gesunken ist.
|
Lineare Differenzengleichung (Rekursive Darstellung) Bei linearem Wachstum bzw. linearer Abnahme gilt für einen Bestand $y_t$ nach $t$ Zeitschritten:
mit konstanter Änderungsrate $k$ und Anfangsbestand $y_0$.
|
Ein Produkt kostet $1000 €$ und wird jährlich um $40 €$ teurer. Stellen Sie eine geeignete Differenzengleichung (Rekursionsgleichung) auf, die diesen Sachverhalt modelliert.
Zunächst benennen wir die Folge mit einer beliebigen Variablen, beispielsweise mit $a$.
Beim Ausgangswert handelt es sich um die ursprünglichen Kosten des Produkts, d. h. $a_0=1000 €$. Der Betrag erhöht sich jährlich um $40 €$, sprich $k=40€$.
Somit gilt: $\boldsymbol{a_0=1000€}$; $\hspace{0.3cm} \boldsymbol{a_{n+1}=a_n+40}$
Folglich beträgt die Differenz zwischen dem nächsten Jahr und dem aktuellen Jahr $40$, oder anders ausgedrückt $a_{n+1}-a_n=40$.
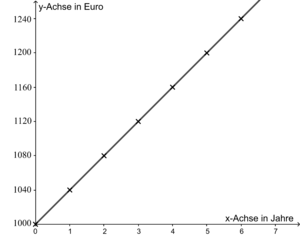
Die Aufgabe lässt sich nun auch noch grafisch darstellen:
Zu Beginn kostet das Produkt $1000€$. Dies entspricht dem Punkt $(0\vert 1000)$ im Koordinatensystem. Nach einem Jahr kostet das Produkt $1040 €$ ($(1\vert 1040)$), nach einem weiteren Jahr bereits $1080$ ($(2\vert 1080)$) usw.
Zur besseren Veranschaulichung wurde die $y$-Achse gestaucht.
Da nun alle eingezeichneten Punkte auf einer Linie liegen, handelt es sich dabei um eine lineare Differenzengleichung.
In einer Regentonne befinden sich $250l$ Regenwasser. Davon werden täglich $15l$ zur Bewässerung der Pflanzen genutzt. Stellen Sie eine geeignete Differenzengleichung (Rekursionsgleichung) auf, die diesen Sachverhalt modelliert.
Wir bezeichnen unsere Folge nun mit $b$. Analog zum vorherigen Beispiel beträgt der Anfangswert $b_0=250l$ und $k=-15$, da es sich nun um eine Abnahme handelt. Es gilt:
$\boldsymbol{b_0=250l \quad, \quad b_{n+1}=b_n-15 \quad}$ bzw. $\boldsymbol{\quad b_{n+1}-b_n=-15}$
Exponentielle Differenzengleichung (geometrische Folge)
Für ein exponentielles Wachstum ist eine konstante prozentuelle Zunahme in gleichen Zeitspannen charakteristisch.
Bei einer exponentiellen Differenzengleichung wächst bzw. sinkt der angegebene Wert mit jedem Folgeglied um denselben Prozentsatz bzw. um denselben relativen Anteil.
|
Exponentielle Differenzengleichung (Rekursive Darstellung) Bei exponentiellem Wachstum bzw. exponentieller Abnahme gilt für einen Bestand $y_t$ nach $t$ Zeitschritten:
mit konstantem Änderungsfaktor $a$ und Anfangsbestand $y_0$.
|
Vera zahlt $2€$ auf ihr Konto ein. Diesen Betrag verdreifacht sie jeden Monat. Stellen Sie eine geeignete Differenzengleichung (Rekursionsgleichung) auf, die diesen Sachverhalt modelliert.
Da sich der Kontostand monatlich verdreifacht, muss dieser mit dem Faktor $3$ multipliziert werden. Dabei handelt es sich um den Wachstumsfaktor $a$ in der vorherigen Definition (analog zur Exponentialfunktion). Es gilt:
$\boldsymbol{y_0=2€ \quad , \quad y_{n+1}=y_n\cdot 3\quad}$ mit $\quad \frac{y_{n+1} }{y_n}=3 \qquad$ bzw. $\boldsymbol{\qquad y_{n+1}-y_n=y_n\cdot 2}$.
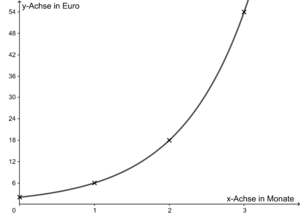
Der Ausdruck $y_{n+1}-y_n=y_n\cdot 2$ beschreibt den Unterschied des Kontostands von einem Monat zum darauffolgenden, beispielsweise vom 6. zum 7. Monat. Dieser beträgt immer das Doppelte des Kontostands vom Ausgangsmonat. Somit erhält man den Kontostand des 7. Monats, indem man zum Kontostand des 6. Monats erneut das Doppelte desselbigen addiert.
Grafische Veranschaulichung:
In einem Waldgebiet mit $20 000$ Bäumen tritt ein Schädling auf, der jährlich $5\%$ der noch nicht geschädigten Bäume befällt. Stellen Sie eine geeignete Differenzengleichung (Rekursionsgleichung) auf, die diesen Sachverhalt modelliert.
Da der Anfangsbestand der Bäume $20 000$ beträgt, gilt $b_0=20 000$. Mithilfe des angegebenen Prozentsatzes können wir nun den Zerfallsfaktor $a$ bestimmen:
$a=1-\frac{p}{100}=1-\frac{5}{100}=0.95$
Der Zerfallsfaktor gibt an, dass nach einem Jahr noch $95\%$ der Bäume nicht befallen sind.
Analog zu oben erhalten wir:
$\boldsymbol{b_0=20 000 \quad , \quad b_{n+1}=b_n\cdot 0.95\quad}$ mit $\quad \frac{b_{n+1} }{b_n}=0.95 \qquad$ bzw. $\boldsymbol{\qquad b_{n+1}-b_n=b_n\cdot (-0.05)}$.
Der Faktor $(-0.05)$ gibt an, dass die Anzahl der noch nicht geschädigten Bäume jährlich um $5\%$ abnimmt.
Quiz: Differenzengleichungen (AN 1.4)