Konfidenzintervall
Einleitendes Video
Einleitung
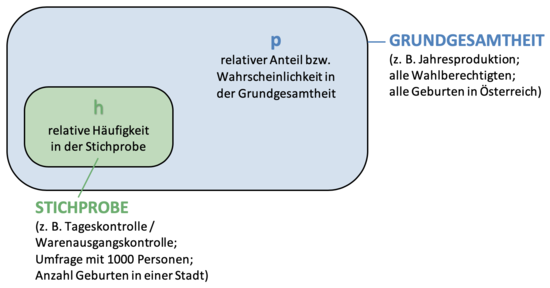
In der beurteilenden Statistik werden Beziehungen zwischen einer Grundgesamtheit und dazugehörigen Stichproben untersucht. Vielfach steht für praktische Anwendungen die Grundgesamtheit nicht oder nicht mehr zur Verfügung. Deshalb werden geeignete Stichproben genutzt, um Rückschlüsse auf die betreffende Grundgesamtheit treffen zu können.
Beispielsweise ist es für eine Wahlprognose zu aufwändig, alle Wähler (= Grundgesamtheit) zu befragen. Stattdessen wird nur eine Stichprobe von Wählern befragt und anschließend wird versucht, von dem Ergebnis der Stichprobe auf die Grundgesamtheit zu schließen.
Problemstellungen
Im Folgenden unterscheiden wir zwei Fragestellungen:
| 1) Bei einer Wahl erhielt die Partei A insgesamt $40,5 \%$ aller Stimmen. Nach dem Auszählen der Stimmen werden zufällig $100$ Stimmzettel ausgewählt. Auf wie vielen Stimmzetteln der Stichprobe wird die Partei A angekreuzt sein? | 2) Bevor die Stimmzettel einer Wahl ausgezählt werden, zieht man $100$ Stimmzettel zufällig aus den Wahlurnen. Auf $44$ Stimmzetteln ist die Partei A angekreuzt. Welchen Stimmenanteil hat diese Partei in der Gesamtheit erreicht? |
1) Von der Gesamtheit auf die Stichprobe - Schätzbereich
Die zugrundeliegende Erfolgswahrscheinlichkeit der Gesamtheit $p$ und der Stichprobenumfang $n$ sind bekannt. Es sei $H$ die absolute Häufigkeit der Partei-A-Wähler in der Stichprobe. Es soll ein $\gamma$-Schätzbereich ermittelt werden.
|
$\gamma$-Schätzbereich Das symmetrisch um $p$ liegende Intervall, welches die unbekannte relative Häufigkeit $h$ mit der Wahrscheinlichkeit (Sicherheit) $\gamma$ enthält, heißt $\gamma$-Schätzbereich. |
Im Beispiel mit $n=100$ und $p=0.405$ soll ein $90\%$-Schätzbereich um den Erwartungswert $\mu$ ermittelt werden. Wegen $n\cdot p\cdot (1-p) > 9$ darf die Binomialverteilung näherungsweise durch eine Normalverteilung ersetzt werden.
Zunächst ermitteln wir den Erwartungswert $\mu$ und die Standardabweichung $\sigma$:
$$\mu=n\cdot p=100\cdot 0.405=40.5 \quad \text{und} \quad \sigma=\sqrt{n\cdot p\cdot (1-p)}\approx 4.91$$
Für einen $90\%$-Schätzbereich um $\mu$ gilt:
$$P(x_{min}\leq H \leq x_{max})=0.9$$
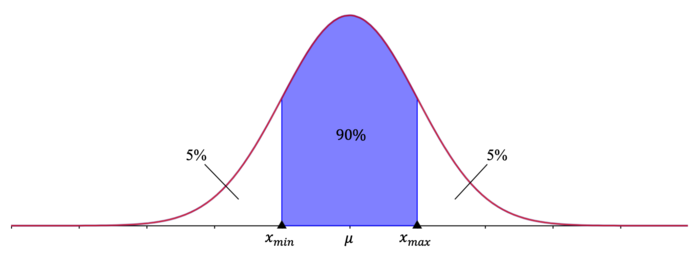
Zur Ermittlung der gesuchten Intervallgrenzen $x_{min}$ und $x_{max}$ verwenden wir nun zwei Eigenschaften des Graphen der Dichtefunktion:
1) Die gesamte Fläche unterhalb der Dichtefunktion ist $1$, sie entspricht also $100\%$.
2) Die Glockenkurve ist symmetrisch um den Erwartungswert $\mu$.
Aus den genannten Eigenschaften folgt, dass die beiden Flächenstücke links und rechts von der blau markierten Fläche jeweils $5\%$ einnehmen.
Mithilfe von Technologieeinsatz können wir somit die beiden Intervallgrenzen $x_{min}$ und $x_{max}$ ermitteln:
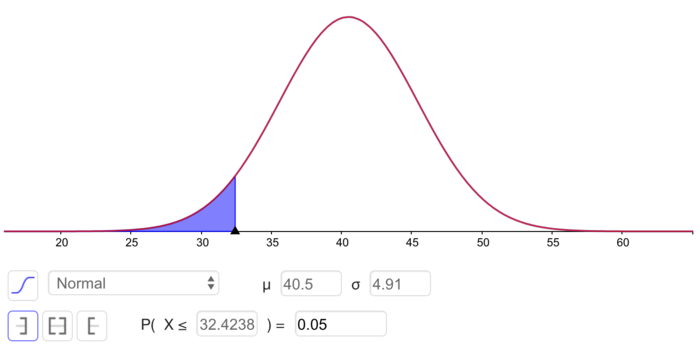
$P(H\leq x_{min})=0.05 \Rightarrow \boldsymbol{x_{min}\approx 32 }$
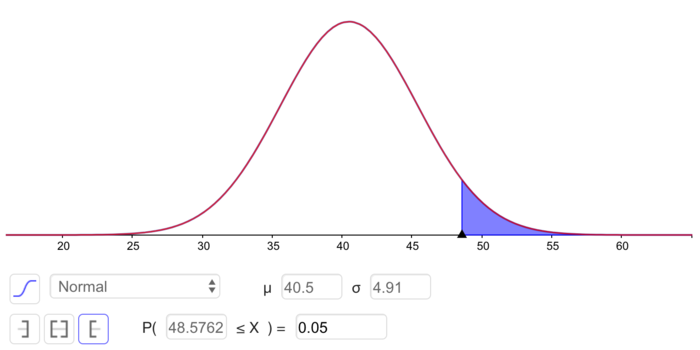
Da die beiden Werte symmetrisch zum Erwartungswert liegen, muss auch deren Abstand derselbe sein. Der Abstand von $x_{min}$ zum Erwartungswert $\mu$ beträgt $\mu-x_{min}=40.5-32.42=8.08$. Daraus resultiert für
$\boldsymbol{x_{max}=\mu + 8.08=48.58 \approx 49 }$
Antwort: Die Anzahl der in der Stichprobe für die Partei A abgegebenen Stimmen wird mit $90\%$-iger Wahrscheinlichkeit zwischen $32$ und $49$ liegen, wobei $32$ nicht unter- und $49$ nicht überschritten wird.
Alternativ erhält man als $\gamma$-Schätzbereich für die relative Häufigkeit $h$ in einer Stichprobe näherungsweise
$h\approx\left[p-z\cdot \sqrt{\left(\frac{p\cdot (1-p)}{n}\right)}; p+z\cdot \sqrt{\left(\frac{p\cdot (1-p)}{n}\right)}\right] \qquad$ mit $\quad 2 \Phi(z)-1=\gamma \qquad$ (siehe Formelsammlung)
$n$ … Stichprobenumfang
$h$ ... unbekannte relative Häufigkeit in einer Stichprobe
$p$ ... relativer Anteil in der Grundgesamtheit
$\gamma$ ... Wahrscheinlichkeit
Für die Berechnung von $0.90$- bzw. $0.95$- bzw. $0.99$-Schätzbereichen kann man sich merken:
| Zu $\gamma=0.9$ gehört $z=1.645 \qquad$ | Zu $\gamma=0.95$ gehört $z=1.96 \qquad$ | Zu $\gamma=0.99$ gehört $z=2.576 \qquad$ |
Hinweis: Bei anderen Konfidenzniveaus – welche in der Regel im Schulgebrauch nicht vorkommen – muss für die Ermittlung des Verteilungswerts $z$ die Tabelle der Standardnormalverteilung herangezogen werden.
Auf das Beispiel angewendet erhält man somit
$h\approx \left[0.405-1.645\cdot\sqrt{\left(\frac{0.405\cdot (1-0.405)}{100}\right) }; 0.405-1.645\cdot\sqrt{\left(\frac{0.405\cdot (1-0.405)}{100}\right)}\right]$
$h\approx[0.324; 0.486]\Rightarrow \boldsymbol{H\approx [32; 49]}$
Eine weitere Möglichkeit zur Ermittlung des gesuchten $90\%$-Schätzbereichs bietet GeoGebra im CAS-Modus mit dem Befehl {GaußAnteilSchätzer( <Stichprobenanteil>, <Stichprobengröße>, <Signifikanzniveau> )}:
Anmerkungen: Neben obigem Beispiel zum $\gamma$-Schätzbereich lassen sich noch zwei weitere, durchaus relevante Typen von Fragestellungen formulieren:
- Mit welcher Wahrscheinlichkeit findet man unter einer Stichprobe von $100$ zufällig ausgewählten Stimmzetteln zwischen $32$ und $49$ Partei-A-Wähler? ($n$ und Intervall gegeben, $\gamma$ gesucht)
- Wie viele Stimmzettel muss man zufällig auswählen, damit man mit $90 \%$iger Wahrscheinlichkeit zwischen $32$ und $49$ Partei-A-Wähler in der Stichprobe hat? ($\gamma$ und Intervall gegeben, $n$ gesucht)
2) Von der Stichprobe auf die Gesamtheit - Konfidenzintervall
Die zugrundeliegende Erfolgswahrscheinlichkeit der Gesamtheit ist nicht bekannt. Sie muss aus der relativen Häufigkeit der Stichprobe geschätzt werden.
|
$\gamma$-Konfidenzintervall (Sicherheits- bzw. Vertrauensintervall) Die Menge aller Schätzwerte für $p$, deren zugehörige $\gamma$-Schätzbereiche den in der Stichprobe beobachteten Wert $h$ überdecken, heißt Konfidenzintervall mit Sicherheit $\gamma$ ($\gamma$-Konfidenzintervall oder Vertrauensintervall zum Konfidenzniveau $\gamma$) für den unbekannten relativen Anteil $p$. |
Es soll nun ein $90\%$-Konfidenzintervall, also ein Schätzbereich, der mit einer Wahrscheinlichkeit von $90\%$ den gesuchten wahren Wert beinhaltet, für den relativen Anteil $p$ in der Grundgesamtheit ermittelt werden.
Analog zum $\gamma$-Schätzbereich ist die Näherungsformel zur Bestimmung des $\gamma$-Konfidenzintervalls für den relativen Anteil $p$ in der Grundgesamtheit ausreichend. Es gilt:
$ p\approx \left[h-z\cdot\sqrt{\left(\frac{h\cdot (1-h)}{n}\right) }; h+z\cdot \sqrt{ \left(\frac{h\cdot (1-h)}{n}\right) } \right] \qquad $ mit $\quad 2 \Phi(z)-1= \gamma \qquad$ (siehe Formelsammlung)
$n$ … Stichprobenumfang
$h$ ... relative Häufigkeit in einer Stichprobe
$p$ ... unbekannter relativer Anteil in der Grundgesamtheit
$\gamma$ ... Konfidenzniveau (Vertrauens- bzw. Sicherheitsniveau)
Auch für die Berechnung von $0.90$- bzw. $0.95$- bzw. $0.99$-Konfidenzintervallen gilt:
| Zu $\gamma=0.9$ gehört $z=1.645\qquad$ | Zu $\gamma=0.95$ gehört $z=1.96\qquad$ | Zu $\gamma=0.99$ gehört $z=2.576\qquad $ |
Auf das Beispiel angewendet erhält man somit mit $n=100; h=\frac{44}{100}=0.44$ und $z=1.645$ für
$p\approx \left[0.44-1.645\cdot\sqrt{\left(\frac{0.44\cdot (1-0.44)}{100}\right)}; 0.44-1.645\cdot\sqrt{\left(\frac{0.44\cdot (1-0.44)}{100}\right)}\right]$
$\boldsymbol{p\approx[0.358; 0.522]}$
Antwort: In der Gesamtheit wird der Anteil der Stimmen für die Partei A mit der Wahrscheinlichkeit $0.90$ ungefähr im Intervall $[0.36;0.52]$ liegen.
Auch hier kann zur Ermittlung des gesuchten $90\%$-Konfidenzintervalls der GeoGebra-Befehl GaußAnteilSchätzer( <Stichprobenanteil>, <Stichprobengröße>, <Signifikanzniveau> ) verwendet werden:
|
Wichtige Eigenschaften:
|
Quiz: Konfidenzintervalle (WS 4.1)