Integration: Berechnung von Flächen zwischen zwei Kurven
Inhaltsverzeichnis
Wiederholung und Herleitung der Formel
| Das folgende Video bietet dir einen Überblick über das gelernte und erklärt dir die Formel für die Fläche zwischen 2 Kurven: |
| ab Minute 3:23 geht es um die Fläche zwischen 2 Kurven. |
|
Formel zur Berechnung der Fläche zwischen 2 Graphen
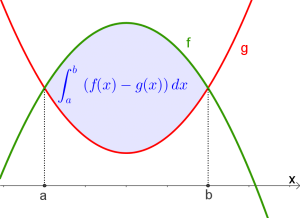
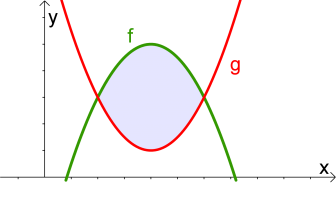
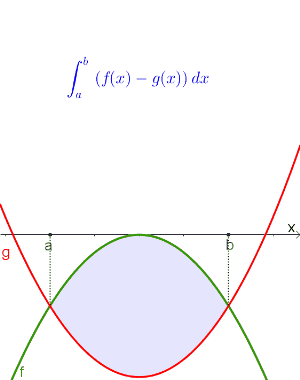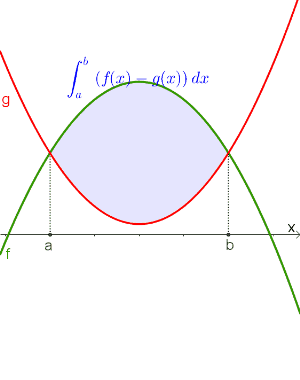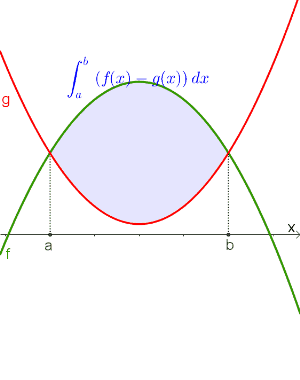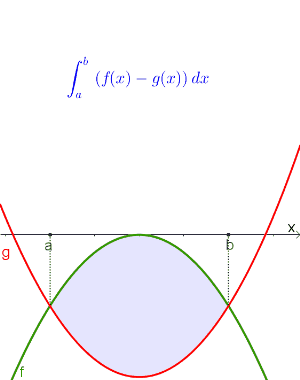
Gegeben sei eine Fläche zwischen zwei Funktionsgraphen $f$ und $g$, dann kann der Inhalt der eingeschlossenen Formel mit dieser Formel berechnet werden: $$\int_a^b f(x)dx-\int_a^b g(x)dx \textrm{ bzw. } \int_a^b \left(f(x)-g(x)\right)dx$$ wobei der Graph von $f$ die obere und der Graph von $g$ die untere Begrenzungskurve sein muss! $$\int_{\color{blue}{linke\ Schnittstelle} }^{\color{blue}{rechte\ Schnittstelle} } \left(\color{green}{obere\ Funktion}-\color{red}{untere\ Funktion}\right)dx$$ |
$Aha!$ Das folgende Applet zeigt dir die Herleitung dieser Formel
Herleitung der Formel als Bilderreihe
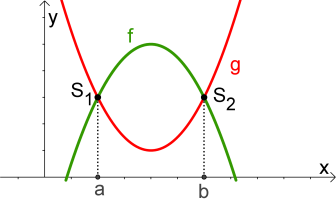
Zuerst werden die Schnittpunkte bestimmt.
Als nächstes berechnet man die große Fläche mit $\int_a^b f(x) dx$ und ...
... zieht davon die kleine Fläche $\int_a^b g(x)dx$ ab.
Als Ergebnis erhält man die gesuchte blaue Fläche.
|
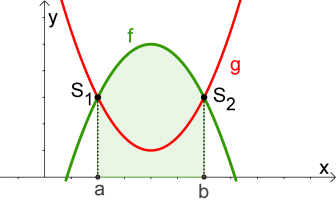
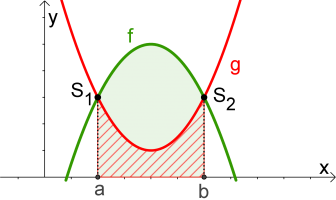
$$\int_a^b f(x)dx-\int_a^b g(x)dx$$ gilt immer! |
Exkurs: Wie werden Schnittpunkte berechnet und warum sind diese wichtig?
Schnittpunkt zweier Funktionen
|
Schnittpunkte sind wichtig, weil sie uns zeigen, in welchem Bereich wir integrieren müssen. |
Beispiele
Berechnen Sie den Inhalt der Fläche, die von den Funktionen f und g umschlossen wird.
$f(x)=x^2$
$g(x)=4$
$$f(x)=g(x)$$ $$x^2=4$$ $$x=\pm 2$$ Somit haben wir einen Schnittpunkt bei $x=-2$ und einen bei $x=2$ (Hinweis: Die y-Koordinaten sind für die weitere Berechnung nicht erforderlich!).
2. Schritt: Flächen berechnen und voneinander abziehen:
Fläche unter $f(x)=A_{\cup}$
Fläche unter $g(x)=A_{ \Box }$
Dann ist die gesuchte Fläche $A$:
$$A=A_{ \Box }-A_{\cup}$$
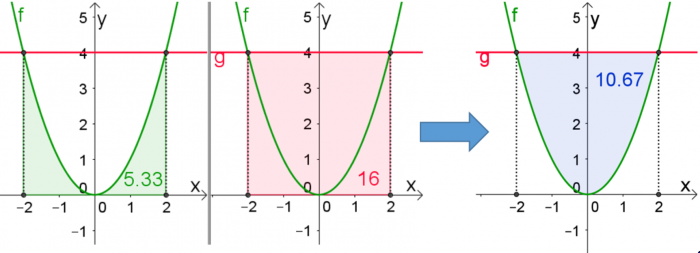
$A_{ \Box }=a*a=4*4=16$
Alternativ kann man hier auch das bestimmte Integral verwenden:
$$A_{ \Box }=\int_{-2}^2 g(x)dx=\int_{-2}^2 4dx=\left[ 4x\right]_{-2}^2=4\cdot 2-\left[ 4\cdot (-2)\right]=\underline{16}$$
$$A_{\cup}=\int_{-2}^2 f(x)dx=\int_{-2}^2 x^2dx=\left[\frac{x^3}{3}\right]_{-2}^2=\frac{2^3}{3}-\frac{(-2)^3}{3}=\frac{16}{3}=\underline{5.33}$$
Damit erhält man für $A$: $$A=A_{ \Box }-A_{\cup}=\int_{-2}^2 g(x)dx-\int_{-2}^2 f(x)dx$$ $$A=16-5,33=\underline{\underline{10,67} }$$ Wichtig: Da hier der Graph von $g$ oberhalb von $f$ liegt, muss man die Formel wie hier gezeigt anschreiben!
In den folgenden Beispielen wenden wir nun direkt die Formel an, ohne die Einzelheiten zu erklären:
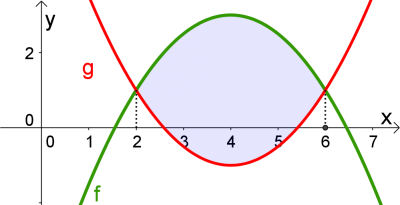
Berechne den Inhalt der Fläche, die von den beiden Funktionsgraphen mit $f(x)=-0.5 x² + 4x - 5$ und $g(x)=0.5x² - 4x + 7$ eingeschlossen wird. Fertige zuerst eine Skizze.
1. Schritt: Schnittpunkte $$f(x)=g(x)$$ $$-0.5 x² + 4x - 5=0.5x² - 4x + 7$$ $$0=x^2-8x+12$$ $$x_1=2\textrm{ und } x_2=6$$
2. Schritt: Anwenden der Formel $$\int_a^b \left(f(x)-g(x)\right)dx$$ $$\int_2^6 \left((-0.5 x² + 4x - 5)-(0.5x² - 4x + 7))\right)dx$$ $$\int_2^6 \left(-x^2+8x-12\right)dx=10.67$$
Der gesuchte Flächeninhalt beträgt 10.67 FE.
|
Wichtig ist immer, dass in der Formel immer die obere Funktion minus die untere Funktion berechnet wird.
Besteht eine Fläche aus mehreren Teilschnittflächen, so muss in der Regel jede einzeln berechnet werden! |
Dies muss in Beispielen wie dem folgenden berücksichtigt werden:
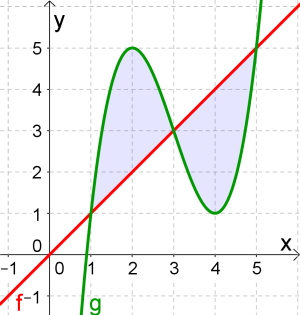
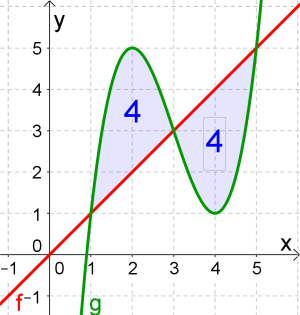
Berechne den Inhalt der blau eingefärbten Fläche, wobei $f(x)=x$ und $g(x)=x^3-9x^2+24x-15$ ist.
$$f(x)=g(x)$$ $$x=x^3-9x^2+24x-15$$ Mithilfe von Technologie erhält man: $$x_1=1,\ x_2=3 \textrm{ und } x_3=5$$
2. Schritt: Berechnung des Flächeninhaltes
Die gesuchte Fläche besteht aus zwei Flächeninhalten, die wir getrennt von einander berechnen würden, weil f und g abwechselnd oben bzw. unten sind.
Die Rechnung $\int_1^5 (f(x)-g(x))dx$ wäre <span style="color=red" falsch</span>, da hier 0 herauskommt (prüfe es selbst nach!)
- Linke Fläche: Hier ist g oben und f unten:
$$\int_1^3 (g(x)-f(x))dx=\int_1^3 (x^3-9x^2+24x-15-x)dx=\underline{4}$$
- Rechte Fläche: Hier ist f oben und g unten:
$$\int_3^5 (f(x)-g(x))dx=\int_1^3 (x-(x^3-9x^2+24x-15))dx=\underline{4}$$
- Gesamt: $4+4=\underline{\underline{8} } $
Die eingeschlossene Fläche hat 8 FE.
Übungs- und Lernlinks
- Erklärungen und Beispiele von brinkmann-du
- Erklärung von matheguru
- Beispiele samt Lösungen von Roolfs
- weiters Lernvideo in dem ein Beispiel vorgerechnet wird
