Inhalt:Integration: Idee der Integration: Fläche als Summe unendlich kleiner Rechtecke
Ober- und Untersummen
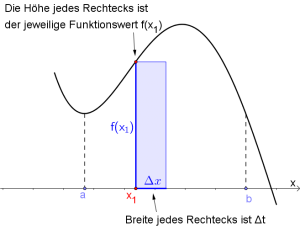
In diesem Kapitel wollen wir die tatsächliche Fläche unter einer Kurve annähernd berechnen (siehe Abbildung oben). Dies machen wir auf zwei Arten:
a) Wir zeichnen viele Rechtecke unter die Kurve (siehe Abbildung) und addieren dann Rechtecksflächen (= Untersumme). Damit erhalten wir eine Fläche die sicherlich kleiner als die tatsächliche Fläche unter der Kurve ist.
b) Nun zeichnen wir viele Rechtecke über die Kurve und addieren dann wieder die Rechtecksflächen (= Obersumme). Das Ergebnis muss größer sein, als der tatsächliche Inhalt unter der Kurve.
Wie können wir damit aber den tatsächlichen Flächeninhalt unter der Kurve berechnen?
|
Die Idee ist nun, beliebig viele Rechtecke einzuschreiben.
$Aha!$ $\ $ Wie du an diesem Applet erkennen kannst, nähern sich die Ober- und Untersumme immer mehr dem tatsächlichen Flächeninhalt an. |
Wie ist dieses Applet zu bedienen?
- Klicke links unten auf das „Play“-Symbol oder verschiebe den Schieberegler „Rechtecksanzahl“.
- Beobachte, wie sich die Untersumme immer mehr der tatsächlichen Fläche annähert.
- Klicke dann auf das Kästchen „Obersumme“ und wiederhole hier die Schritte 1 und 2.
Die orientierte Fläche unter einer Kurve kann somit als Grenzwert (= Limes) der Summe von unendlich vielen Rechtecken mit der Höhe $f(x)$ und einer unendlich kleinen Breite berechnet werden.
Formale Berechnung und Schreibweise
Die Berechnung der Ober- und Untersumme funktioniert nun folgendermaßen:
- Zuerst berechnen wir die Fläche eines der Rechtecke. Dieses hat die Breite $\Delta x$ und die Höhe $f(x_1)$ (da die Höhe an der Stelle $x_1$ ja dem Funktionswert von $f$ entspricht). Somit gilt: $$Inhalt\ eines\ Rechtecks=f(x_1)\cdot \Delta x$$
- Dann summieren wir über alle Rechtecke, um die Unter- bzw. Obersumme zu erhalten: $$\sum_{i=1}^{n} f(x_i)\cdot \Delta x$$
- Im letzten Schritt bilden wir unendlich viele Summen, da wir aus dem vorigen Applet wissen, dass wir damit der tatsächlichen Fläche beliebig nahe kommen:
$$\lim_{n\rightarrow \infty}\sum_{i=1}^{n}\underbrace{f(x_i)\cdot \Delta x}_{\textrm{Fläche eines Rechteckes}}=\int_{a}^{b} f(x)\cdot dx$$ Der letzte Term $\int_{a}^{b} f(x)\cdot dx$ ist nun die verkürzte Schreibweise für „die unendliche Summe aller Rechtecksinhalte zwischen $a$ und $b$“. Der Term $\int_{a}^{b} f(x)\cdot dx$ wird so ausgesprochen: „das Integral zwischen $a$ bis $b$ von $f(x)$ mal $dx$“
Bedeutung der einzelnen Terme: $$\lim_{n\rightarrow \infty}\sum_{i=1}^{n} f(x_i)\cdot \Delta x=\int_{a}^{b} f(x)\cdot dx$$
- $f(x_i)$...Höhe eines Rechtecks
- $\Delta x$ .... Breite eines Rechtecks
- $f(x_i)\cdot \Delta x$...Fläche eines Rechtecks
- $\sum_{i=1}^{n}$... Summe aller n Rechtecksflächen
- $\int $ unendliche Summe (= Integrationszeichen) und damit eine verkürzte Schreibweise für $\lim_{n\rightarrow \infty}\sum_{i=1}^{n}$
- $dx$...unendlich kleine Breite eines Rechtecks
- $\int_{a}^{b} f(x)\cdot dx$... unendliche Summe aller Rechtecksflächen zwischen $a$ und $b$
$$\int_{a}^{b} f(x)\cdot dx$$
- $f(x)$ heißt Integrand (das, was integriert wird)
- $x$ heißt Integrationsvariable
- $a$ und $b$ heißen untere bzw. obere Integrationsgrenze
- $\int_{a}^{b} f(x)\cdot dx$ ist das bestimmte Integral und gibt die orientierte Fläche zwischen $f(x)$ und der $x$-Achse an.
|
|
Beispiel
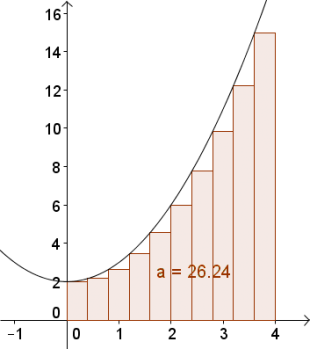
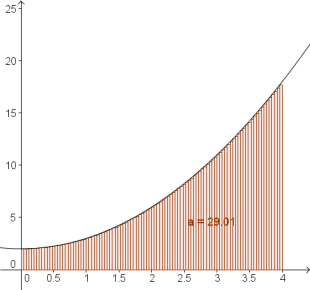
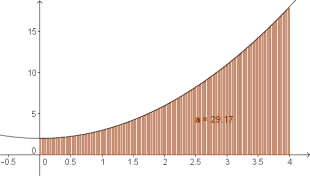
Im folgenden Beispiel ist die Funtkion $f(x)=x^2+2$ gegeben und es wird die Fläche zwischen $0$ und $4$ mithilfe von Rechtecken berechnet. Die tatsächliche Fläche beträgt $a=29.33$ FE.
- Je größer die Anzahl der Rechtecke, desto näher liegt die Untersumme am tatsächlichen Flächeninhalt.