Änderungsmaße

Änderungsmaße

Änderungsmaße

Möchte man Daten miteinander vergleichen oder Änderungen von Größen beschreiben, so können sogenannte Änderungsmaße verwendet werden.

Definition

Änderungsmaße Sei $f$ eine reelle Funktion, die auf dem Intervall $[a; b]$ definiert ist. Dann bezeichnet man die reelle Zahl - $\quad$ $f(b)-f(a) \hspace{1cm}$ als absolute Änderung von $f$ in $[a; b]$. - $\quad$ $\frac{f(b)-f(a)}{f(a)} \hspace{1.6cm}$ als relative Änderung von $f$ in $[a; b]$. - $\quad$ $\frac{f(b)-f(a)}{f(a)}\cdot 100 \hspace{0.6cm}$ als prozentuelle Änderung von $f$ in $[a; b]$. - $\quad$ $\frac{f(b)-f(a)}{b-a} \hspace{1.65cm}$ als mittlere Änderungsrate (oder Differenzenquotient) von $f$ in $[a; b]$. - $\quad$ $\frac{f(b)}{f(a)} \hspace{2.35cm}$ als Änderungsfaktor von $f$ in $[a; b]$. Anmerkung: Der Änderungsfaktor ist immer um $1$ größer als die relative Änderung: $\frac{f(b)-f(a)}{f(a)}=\frac{f(b)}{f(a)}-\frac{f(a)}{(f(a)}=\frac{f(b)}{f(a)}-1$

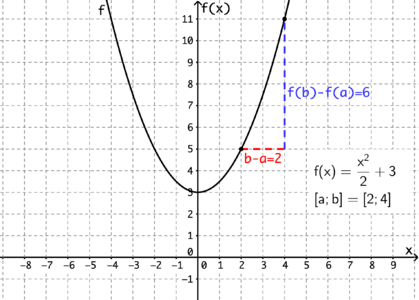
Gegeben ist die Funktion $f$ mit der Funktionsgleichung $f(x)=\frac{x^2}{2}+3$.

$\hspace{2.15cm}$Aufgabenstellung:
$\hspace{2.05cm}$ Berechnen Sie (1) die absolute, (2) die relative und (3) die prozentuelle Änderung sowie (4) den Änderungsfaktor von $f$ im
$\hspace{2.05cm}$ Intervall $[2; 4]$.

(1) Absolute Änderung: $f(b)-f(a)=f(4)-f(2)=\frac{4^2}{2}+3-(\frac{2^2}{2}+3)=(8+3)-(2+3)=6$
Der Funktionswert nimmt in diesem Intervall absolut um $6$ zu.

(2) Relative und (3) prozentuelle Änderung: $\frac{f(b)-f(a)}{f(a)}=\frac{f(4)-f(2)}{f(2)}=\frac{6}{5}=1.2\Rightarrow 1.2\cdot 100=120\%$
Der Funktionswert nimmt in diesem Intervall um $120\%$ zu.

(4) Änderungsfaktor: $\frac{f(b)}{f(a)}=\frac{4}{2}=\frac{11}{5}=2.2$
Man muss $f(2)$ mit $2.2$ multiplizieren um $f(4)$ zu erhalten.

Eine Funktion $s:[0;6]\rightarrow \mathbb{R}$ beschreibt den von einem Radfahrer innerhalb von $t$ Sekunden zurückgelegten Weg. Es gilt: $s(t)=\frac{1}{2}t^2+2t$
Der zurückgelegte Weg wird dabei in Metern angegeben, die Zeit wird ab dem Zeitpunkt $t_0=0$ in Sekunden gemessen.

$\hspace{2.05cm}$ Aufgabenstellung:
$\hspace{2.05cm}$ Ermitteln Sie den Differenzenquotienten der Funktion $s$ im Intervall [0; 6] und deuten Sie das Ergebnis.

$\frac{s(6)-s(0)}{6-0}=\frac{30-0}{6}=5$

Interpretation: Die mittlere (durchschnittliche) Geschwindigkeit des Radfahrers im Zeitintervall $[0;6]$ Sekunden beträgt $5 m/s$.

Aufgrund einer Beförderung erhöht sich das Gehalt eines Angestellten von $2 400€$ auf $2 760€$.

Aufgabenstellung:
$\hspace{2.05cm}$ Um wie viel Prozent ist sein Gehalt gestiegen?

Lösungsansatz mithilfe der relativen bzw. prozentuellen Änderung:

$\frac{f(b)-f(a)}{f(a)}=\frac{Endgehalt-Ausgangsgehalt}{Ausgangsgehalt}=\frac{2 760€-2 400€}{2 400€}=0.15$

Sein Gehalt ist somit um $15\%$ gestiegen.

Lösungsansatz mithilfe des Änderungsfaktors:
$\frac{f(b)}{f(a)}=\frac{Endgehalt}{Ausgangsgehalt}=\frac{2 760€}{2 400€}=1.15$

Sein Gehalt ist somit auf das $1.15$-Fache angestiegen. Darüber hinaus entsprechen der Dezimalzahl $1.15$ umgerechnet $115\%$. Da wir beim Änderungsfaktor immer von $100\%$ ausgehen, bedeutet dies einen Anstieg des Gehalts um insgesamt $15\%$.

Die Aufgabe kann also sowohl mit der relativen bzw. prozentuellen Änderung, als auch mit dem Änderungsfaktor gelöst werden.