Theorie Zahlenmengen (1.1.): Unterschied zwischen den Versionen
(→a) Zuordnung) |
(→a) Zuordnung) |
||
| Zeile 198: | Zeile 198: | ||
</div> | </div> | ||
| − | [[Kategorie | + | [[Kategorie: Zahlen und Maße]] |
Version vom 26. September 2013, 17:28 Uhr
Inhaltsverzeichnis
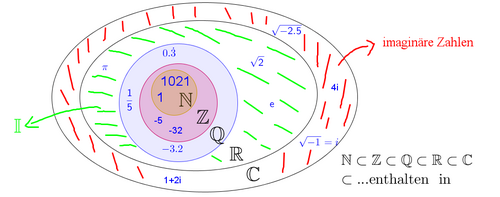
Was haben 2, -8, 3.5 oder $\sqrt{7}$ gemeinsam?
Es sind alles Zahlen. Allerdings sind sie unterschiedlich.
- Einerseits ist ihr Wert unterschiedlich (2 ≠ -8 ≠ 3.5 ≠ $ \sqrt{7} $).
- Andererseits gehören die Zahlen unterschiedlichen Zahlenmengen an.
die natürlichen Zahlen $\mathbb{N}$
| Definition: | Die natürlichen Zahlen $\mathbb{N}$ sind die Zahlenmenge $\mathbb{N}$ ={0,1,2,3,.....} |
Sie sind "abgeschlossen" bezüglich der Addition. Das heißt, wenn man zwei natürliche Zahlen addiert, so landet man wieder bei einer natürlichen Zahl.
Beispiel: $ 7+15=22 $
Sowohl die beiden Summanden links, als auch die Summe rechts sind natürliche Zahlen. Es ist nicht möglich, zwei natürliche Zahlen zu addieren und dabei eine "nicht-natürliche" Zahl zu erhalten.
die ganzen Zahlen $\mathbb{Z}$
| Definition: | Die ganzen Zahlen $\mathbb{Z}$ sind die Zahlenmenge $\mathbb{Z}$ ={...,-3,-2,-1,0,1,2,3,.....}. |
Beachte, dass jede natürliche Zahl auch eine ganze Zahl ist! Um auf die ganzen Zahlen zu kommen, fügt man den natürlichen Zahlen eifnach alle negativen ganzen Zahlen hinzu.
$\mathbb{Z}$ ist "abgeschlossen" bezüglich der Addition und der Subtraktion.
Beispiele
- $-3+7=4$
- $ -8-17=-25$
Was ist nun aber, wenn man zwei ganze Zahlen dividiert? Beispiel: $$ -2:4= \frac{-2}{4}=-\frac{1}{2} $$ Die Zahl$ -\frac{1}{2} $ ist ein Bruch und sicherlich keine ganze Zahl mehr. Hier sind wir in der nächsten Zahlenmenge gelandet:
Deshalb fügt man nun zu den ganzen Zahlen alle Brüche hinzu und erhält.
die rationalen Zahlen $\mathbb{Q} $
| Definition: | Zu den rationalen Zahlen gehören alle Brüche mit Zähler und Nenner aus den ganzen Zahlen, wobei im Nenner natürlich keine 0 stehen darf. Formal kann man das folgendermaßen schreiben: $$ \mathbb{Q} = \left\{ \frac{a}{b} | a,b \in \mathbb{Z}, b \neq 0\right\} $$ |
Da man jeden Bruch in eine endliche oder unendlich periodische Dezimalzahl verwandeln kann, indem man Zähler mit Nenner dividiert, gehören zu $\mathbb{Q} $ auch alle endlichen ODER unendlich periodischen Dezimalzahlen
Beispiel: $$ \frac{1}{3}=0.333333...$$
oder
$$ \frac{1}{5}=1:5=0.2 $$
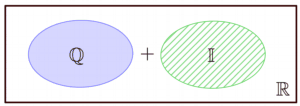
Nun gibt es aber noch Dezimalzahlen, die undendlich lang, aber niemals periodisch sind, diese liegen außerhalb von $\mathbb{Q} $ und heißen die irrationalen Zahlen $\mathbb{I}$
die irrationalen Zahlen $\mathbb{I}$
| Definition: | Zu den irrationalen Zahlen $\mathbb{I}$ gehören alle Dezimalzahlen, die undendlich lang UND niemals periodisch sind |
Beispiele:
- $0,1001000100001....$ (immer eine 0 mehr)
- $\pi =3.14159.... $
- $e =2.718...$, die eulersche Zahl
- $\sqrt{2}=1.414...$ (und alle weiteren Wurzeln von Primzahlen).
die reellen Zahlen $\mathbb{R}$
Fasst man nun alle Dezimahlzahlen zusammen, die
- endlichen oder unendlich periodischen und die
- unendlichen aber niemals periodischen
so erhält man die reellen Zahlen
| Definition: | $$ \mathbb{R} = \mathbb{Q} \cup \mathbb{I} $$ Vereinfacht gesagt: $ \mathbb{R}= $ alle Dezimalzahlen. |
die imaginären Zahlen
Stoff der 2. Klasse
Während in den reellen Zahlen $\mathbb{R}$ addiert, subtrahiert, multipliziert und dividiert werden kann, kann man aber NICHT die Wurzel aus negativen Zahlen berechnen.
Beispiel:
$ \sqrt{-1} $
Aus diesem Grund erweitert man die reellen Zahlen mit allen negativen Wurzeln und nennt
| Definition: | \begin{align} \textrm{die imaginären Zahlen} &=& \textrm{die Menge der negativen Wurzeln} \\ &=&\left\{ \sqrt{-b}\; | b\in \mathbb{R^{+}}\right\}\end{align} |
Weitere Beispiele:
- $ \sqrt{-1}=i$
- $ \sqrt{-4}=4i\ \ $ (weil $\sqrt{4\cdot (-1)}= \sqrt{4}\cdot \sqrt{-1}=2\cdot i $)
Imaginäre Zahlen treten bei den quadratischen Gleichungen auf, wenn die entsprechende Parabel keine Nullstelle hat.
die komplexen Zahlen $\mathbb{C}$
Die komplexen Zahlen $\mathbb{C}$ erhält man, wenn man die reellen Zahlen $\mathbb{R}$ und die imaginären Zahlen zusammenfügt.
| Definition: | $$ \mathbb{C} = \mathbb{R} \cup \textrm{imaginäre Zahlen}$$ |
Setzt man also eine reelle Zahl (z.B. 5) und eine imaginäre Zahl (z.B. 7i) zusammen, so erhält man die komplexe Zahl $$5+7i$$
Beispiele
- 2 + 3i
(jede komplexe Zahl besteht aus einer reellen Zahl, dem sogenannten Realteil (hier: 2) und einer imaginären Zahl (hier 3i), wobei 3 der sogennante Imaginärteil ist.
- -9+18i (Realteil=-9 und Imaginärteil=18)
- 4 $\ \ $ (hier ist der Imaginärteil 0)
- 8i $\ \ $(hier ist der Realteil 0)