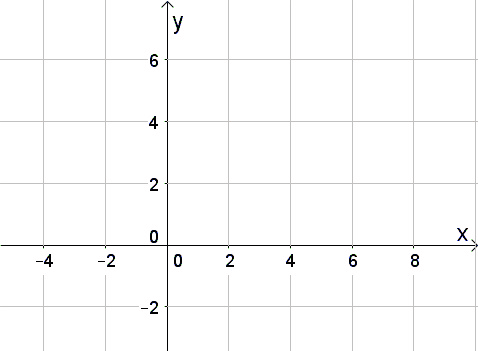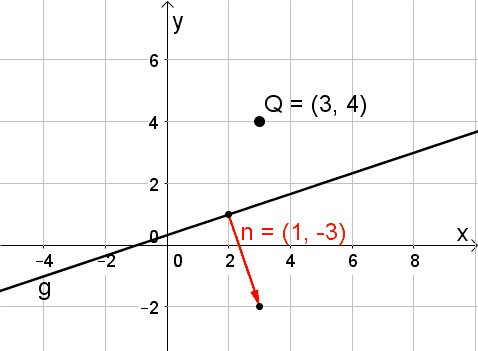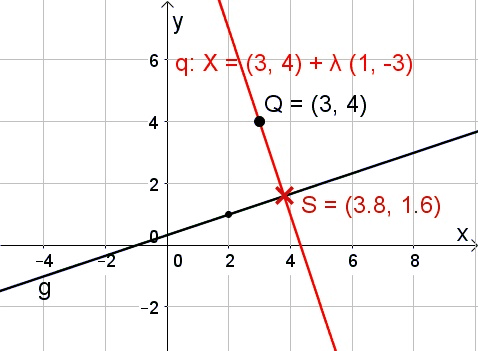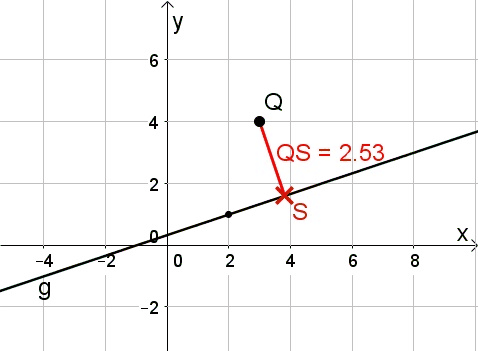Vektorrechnung
Koordinatensystem
Für die Vektorrechnung sind Koordinatensysteme essentiell. Im zweidimensionalen Raum besitzt ein Koordinatensystem $2$ Achsen:
- die $x$-Achse (waagrecht) und
- die $y$-Achse (senkrecht)
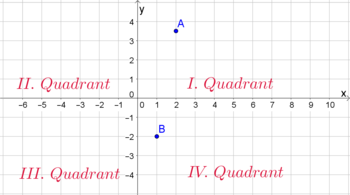
Diese sind unendlich lang und spannen die sogenannten vier Quadranten auf, die meist mit den römischen Ziffern I-IV beschriftet werden (gesprochen: Erster Quadrant, Zweiter Quadrant etc.). Die rechte Grafik zeigt die Positionen der Quadranten. Dort, wo die $2$ Achsen einander treffen, liegt der sogenannte Ursprung (kurz: $\vec{0}$); seine Koordinaten sind $(0|0)$.
Was es außerdem noch zu beachten gibt, hast du vielleicht bereits selbst erkannt:
An den gegenüberliegenden Seiten der $x$- und $y$-Achsen werden unterschiedliche Vorzeichen verwendet. So spricht man „links“ des Ursprungs von der negativen bzw. „rechts“ des Ursprungs von der positiven $x$-Achse. Analog ist mit „oben“ bzw. „unten“ die positive bzw. negative $y$-Achse gemeint.
Im dreidimensionalen Raum kommt eine dritte Achse - die $z$-Achse - dazu. Punkte und Vektoren besitzen dann auch $3$ Koordinaten. Dies kann man bis ins $n$-dimensionale weiterführen.
Punkte
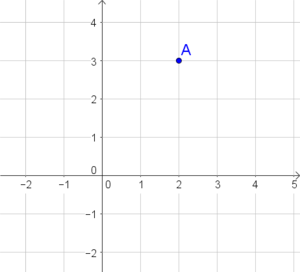
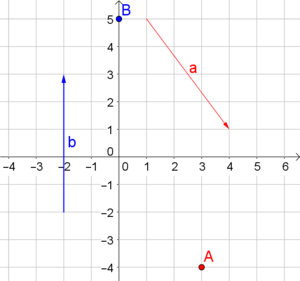
In ein Koordinatensystem lassen sich Punkte eintragen. Diese besitzen, entsprechend ihrer Lage, Koordinaten. Im obigen Bild haben wir beispielsweise die Punkte $A$ und $B$, wobei sich $A$ im ersten und $B$ im vierten Quadranten befindet, eingezeichnet. Man schreibt: $A(2|3.5), B(1|-2)$.
|
Einen allgemeinen Punkt schreibt man an als $P(x_1 \vert x_2 \vert ... \vert x_n)$ (im $n$-dimensionalen Raum $\mathbb{R^n}$) bzw. $P(x \vert y)$ (im $2$-dimensionalen Raum $ \mathbb{R^2}$) oder $P(x \vert y \vert z)$ (im $3$-dimensionalen Raum $\mathbb{R^3}$).
Punkte werden in der Regel mit Großbuchstaben bezeichnet. |
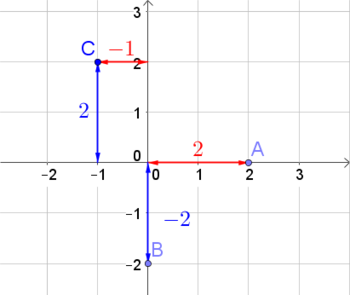
Koordinaten von Punkten lassen sich also ganz einfach ablesen. Die $x$- bzw. $y$-Koordinate entspricht dabei dem Abstand vom Ursprung zum Punkt in Richtung der jeweiligen Koordinatenachse. So erkennen wir im Bild rechts die folgenden Punkte:
- $A($$2$$|$$0$$)$
- $B($$0$$|$$-2$$)$
- $C($$-1$$|$$2$$)$
Inhaltsverzeichnis
- 1 Definition & Darstellung von Vektoren
- 2 Rechnen mit Vektoren
- 3 Mittelpunkt einer Strecke
Definition & Darstellung von Vektoren
|
Ein Zahlenpaar $\vec{v}=\left( \begin{array}{c} x \\ y \end{array} \right) \in \mathbb{R^2}$ wird als Vektor aus $\mathbb{R^2}$ bezeichnet.
Analog bezeichnet man ein Zahlentripel $\vec{v}=\left( \begin{array}{c} x \\ y \\ z \end{array} \right) \in \mathbb{R^3}$ als Vektor aus $\mathbb{R^3}$ . |
Da sowohl die Rechenoperationen, als auch die geometrischen Darstellungen leicht vom $\mathbb{R^2}$ in den $\mathbb{R^3}$ übertragen werden können, werden wir hier meistens nur die Vorgangsweise für Zahlenpaare aus dem $\mathbb{R^2}$ beschreiben.
Geometrische Darstellung von Vektoren
Es gibt zwei Möglichkeiten, wie wir einen Vektor $\vec{v}=\left( \begin{array}{c} a \\ b \end{array} \right) \ \in \mathbb{R^2}$ geometrisch darstellen können:
- Darstellung als Punkt: Dabei gibt $a$ die $x$-Koordinate und $b$ die $y$-Koordinate des Punktes an. Die Beschriftung erfolgt mit Großbuchstaben.
- Darstellung als Pfeil: Dabei gibt $a$ die $x$-Richtung des Pfeils (wie weit zeigt der Pfeil nach links bzw. rechts) und $b$ die $y$-Richtung des Pfeils (wie weit zeigt der Pfeil nach oben bzw. unten) an. Pfeile werden mit Kleinbuchstaben (oft mit Pfeil $\vec{v}$) beschriftet.
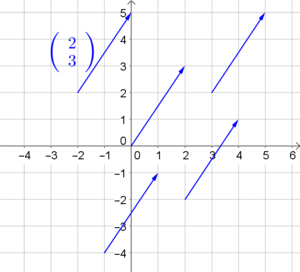
Die Darstellung als Punkt ist eindeutig: Einem Zahlenpaar (= Vektor) entspricht genau ein Punkt.
Die Darstellung als Pfeil ist nicht eindeutig: Es gibt unendlich viele Pfeile, die denselben Vektor darstellen. Diese Pfeile sind aber alle parallel, gleich lang und gleich gerichtet.
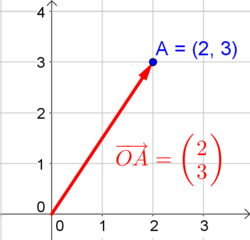
Beispiel: Darstellung des Vektors $\vec{v}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)$
| Punktdarstellung des Vektors | Mögliche Pfeildarstellungen des Vektors |
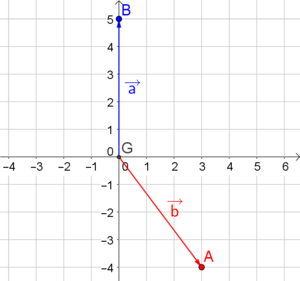
Gegeben seien die Vektoren $\vec{a}=\left( \begin{array}{c} 3 \\ -4 \end{array} \right)$ und $\vec{b}=\left( \begin{array}{c} 0 \\ 5 \end{array} \right)$. Stelle $\vec{a}$ und $\vec{b}$ als Punkte und als Pfeile dar.
Vektoren des $\mathbb{R^3}$ können auch auf diese zwei Arten dargestellt werden. Der einzige Unterschied dabei ist, dass die Punkte bzw. Pfeile im dreidimensionalen Raum liegen. Es gibt also noch eine dritte Richtung, die durch die $z$-Koordinate des Vektors angegeben wird.
Ortsvektoren
Der Ortsvektor von einem Punkt ist der Vektor, der vom Ursprung aus auf den Punkt zeigt. Die Koordinaten bleiben deshalb gleich, es ändert sich quasi nur die Schreibweise:Sei $A(x_1 \vert x_2 \vert ... \vert x_n)$ ein Punkt in der Dimension $n$, dann ist $\vec{0A} = \left( \begin{array}{c} x_1 \\ x_2 \\ ... \\ x_n \end{array} \right)$ dessen Ortsvektor.
Rechnen mit Vektoren
Addition und Subtraktion von Vektoren
Rechnerische Addition
|
Wenn du Vektoren addieren oder subtrahieren möchtest, musst du dazu die entsprechenden Koordinaten addieren: $\left( \begin{array}{c} x_1 \\ x_2 \\ ... \\ x_n \end{array} \right) \pm \left( \begin{array}{c} y_1 \\ y_2 \\ ... \\ y_n \end{array} \right) = \left( \begin{array}{c} x_1 \pm y_1 \\ x_2 \pm y_2 \\ ... \\ x_n \pm y_n \end{array} \right)$ Wichtig ist dabei, dass die Vektoren, die du addieren oder subtrahieren möchtest, derselben Dimension $n$ angehören. D. h. sie haben gleich viele Koordinaten. |
Gegeben seien die beiden Vektoren $\vec{a}=\left( \begin{array}{c} 5 \\ 2 \end{array} \right)$ und $\vec{b}=\left( \begin{array}{c} 1 \\ -3 \end{array} \right)$.
Berechne erst $\vec{a} + \vec{b}$, dann $\vec{a} - \vec{b}$ und zuletzt $\vec{b} - \vec{a}$.
$\vec{a} - \vec{b} = \left( \begin{array}{c} 5 \\ 2 \end{array} \right) - \left( \begin{array}{c} 1 \\ -3 \end{array} \right) = \left( \begin{array}{c} 5-1 \\ 2-(-3) \end{array} \right) = \left( \begin{array}{c} 4 \\ 5 \end{array} \right)$
$\vec{b} - \vec{a} = \left( \begin{array}{c} 1 \\ -3 \end{array} \right) - \left( \begin{array}{c} 5 \\ 2 \end{array} \right) = \left( \begin{array}{c} 1-5 \\ -3-2 \end{array} \right) = \left( \begin{array}{c} -4 \\ -5 \end{array} \right)$
| Übung zur rechnerischen Addition von Vektoren |
|---|
|
|
| Falls das Applet nicht angezeigt wird, klicke hier |
| Übung zur rechnerischen Subtraktion von Vektoren |
|---|
|
|
| Falls das Applet nicht angezeigt wird, klicke hier |
Geometrische Darstellung der Vektoraddition
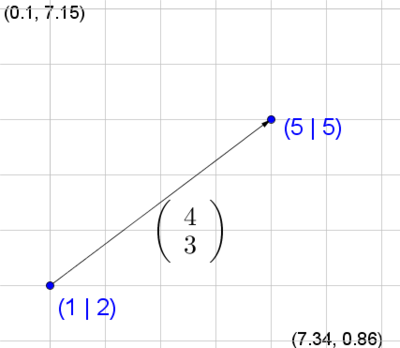
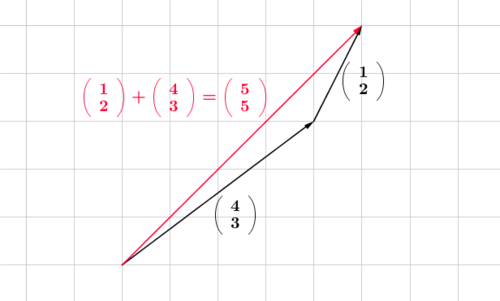
Die Addition zweier Vektoren kann auf zwei verschiedene Arten geometrisch gedeutet werden. Wir illustrieren die beiden Möglichkeiten anhand des Beispiels $\left( \begin{array}{c} 1 \\ 2\end{array} \right) + \left( \begin{array}{c} 4 \\ 3 \end{array} \right)$:
| Punkt + Pfeil - Darstellung: | Pfeil + Pfeil - Darstellung |
| An einen Punkt wird ein Pfeil angehängt. In unserem Beispiel wird an den Punkt $(1 \vert 2)$ ein Pfeil mit der Richtung $\left( \begin{array}{c} 4 \\ 3 \end{array} \right)$ angehängt. Das Ergebnis der Addition ist der Punkt am Ende des Pfeils $(5 \vert 5)$. | Zwei Pfeile werden aneinander gehängt. In unserem Beispiel wird also ein Pfeil mit der Richtung $\left( \begin{array}{c} 4 \\ 3 \end{array} \right)$ und ein Pfeil mit der Richtung $\left( \begin{array}{c} 1 \\ 2 \end{array} \right)$ aneinander gehängt. Das Ergebnis der Addition ist der entstehende Verbindungspfeil mit der Richtung $\left( \begin{array}{c} 5 \\ 5 \end{array} \right)$. |
| Anmerkung: Diese Darstellung ist hilfreich, wenn wir von einem Punkt ausgehen und zu einem neuen Punkt gelangen wollen. | Es spielt keine Rolle, in welcher Reihenfolge die Vektoren angehängt werden. Die Addition ist kommutativ. |
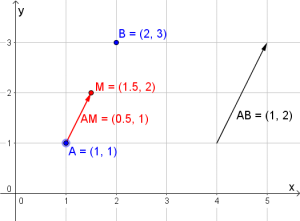
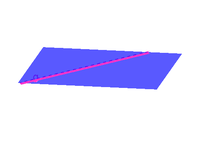
Vektoren bestimmen: „Spitze minus Schaft“ („Ziel minus Start“)
Zwischen $2$ Punkten kann man nun einen Vektor definieren. Dabei gilt die „Spitze minus Schaft“-Regel.
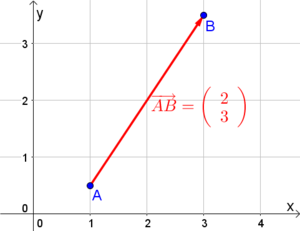
Im Bild rechts wollen wir den Vektor berechnen, der von $A$ nach $B$ geht, also den Vektor $\vec{AB}$. Der Punkt $B(3 \vert 3.5)$ entspricht hierbei der Spitze, und der Punkt $A(1 \vert 0.5)$ dem Schaft. Da das Rechnen mit Punkten allerdings keinen Sinn ergibt, rechnet man stattdessen mit deren Ortsvektoren (siehe oben).
Für unser Beispiel bedeutet das: $\vec{0B} - \vec{0A} = \left( \begin{array}{c} 3 \\ 3.5 \end{array} \right) - \left( \begin{array}{c} 1 \\ 0.5 \end{array} \right) = \left( \begin{array}{c} 3-1 \\ 3.5-0.5 \end{array} \right) = \left( \begin{array}{c} 2 \\ 3 \end{array} \right) = \vec{AB}$
Beachte außerdem:
- Man schreibt der Einfachheit halber oft nur $B-A$, obwohl eigentlich $\vec{0B} - \vec{0A}$ gemeint ist.
- Der Vektor $\vec{AB}$ zeigt in die entgegengesetzte Richtung von $\vec{BA}$. Das bedeutet, dass diese beiden Vektoren entgegengesetzte Vorzeichen haben: $\vec{AB} = - \vec{BA}$
Gegeben sind die Punkte $A(1 \vert 2)$, $B(-3 \vert 1)$ und $C(-4 \vert -1)$. Bilde die folgenden Verbindungsvektoren:
- $\ \vec{AB}$
- $\ \vec{BA}$
- $\ \vec{AC}$
- $\ \vec{BC}$
- $\ \vec{AB}=B-A=\left( \begin{array}{c} -3 \\ 1\end{array} \right) - \left( \begin{array}{c} 1 \\ 2 \end{array} \right)=\left( \begin{array}{c} -4 \\ -1\end{array} \right)$
- $\ \vec{BA}=-\vec{AB}=\left( \begin{array}{c} 4 \\ 1 \end{array} \right)$
- $\ \vec{AC}=\left( \begin{array}{c} -4 \\ -1\end{array} \right) - \left( \begin{array}{c} 1 \\ 2 \end{array} \right)=\left( \begin{array}{c} -5 \\ -3\end{array} \right)$
- $\ \vec{BC}=\left( \begin{array}{c} -4 \\ -1\end{array} \right) - \left( \begin{array}{c} -3 \\ 1 \end{array} \right)=\left( \begin{array}{c} -1 \\ -2\end{array} \right)$
Tipps:
- Pass gut auf die Vorzeichen auf! Beim Subtrahieren von Vektoren passieren leider häufig Vorzeichenfehler. Sei deshalb besonders achtsam.
- Zeichne die Punkte in ein Koordinatensystem und zeichne die Verbindungsvektoren ein. Bei einfachen Koordinaten kannst du den Verbindungsvektor ohne Rechnung ablesen (Probiere es aus!).
Produkt eines Vektors mit einem Skalar
Rechnerische Multiplikation
Wenn man einen Vektor $\vec{v}$ mit einer reellen Zahl $k$, einem sogenannten „Skalar“, multipliziert, werden dabei die einzelnen Koordinaten mit dem Skalar multipliziert:
$k \cdot \vec{v} = k \cdot \left( \begin{array}{c} x_1 \\ x_2 \\ ... \\ x_n \end{array} \right) = \left( \begin{array}{c} k \cdot x_1 \\ k \cdot x_2 \\ ... \\ k \cdot x_n \end{array} \right)$
Gegeben sei der Vektor $\vec{a}=\left( \begin{array}{c} 2 \\ -3 \end{array} \right)$. Multipliziere diesen einmal mit $2$ und einmal mit $-5$.
$(-5) \cdot \vec{a} = (-5) \cdot \left( \begin{array}{c} 2 \\ -3 \end{array} \right) = \left( \begin{array}{c} (-5) \cdot 2 \\ (-5) \cdot (-3) \end{array} \right) = \left( \begin{array}{c} -10 \\ 15 \end{array} \right)$
Geometrische Darstellung der Multiplikation
Eine Multiplikation eines Vektors mit einer reellen Zahl $a$ (Skalar) entspricht einer Streckung (für $|a|>1$) bzw. einer Stauchung (für $|a|<1$) des zugehörigen Pfeiles.
Ist das Vorzeichen des Skalars negativ, so dreht sich die Richtung des Pfeils in die entgegengesetzte Richtung.
Gegeben sei wiederum der Vektor $\vec{a}=\left( \begin{array}{c} 2 \\ -3 \end{array} \right)$. Stelle die Multiplikation mit $2$, mit $-5$ und mit $0.5$ graphisch dar.
- $2 \cdot \vec{a} = \left( \begin{array}{c} 4 \\ -6 \end{array} \right) \rightarrow$ Der Vektor $2\cdot \vec{a}$ hat die doppelte Länge und dieselbe Richtung wie $\vec{a}$.
- $(-5) \cdot \vec{a} = \left( \begin{array}{c} -10 \\ 15 \end{array} \right) \rightarrow$ Der Vektor $(-5)\cdot \vec{a}$ ist fünfmal so lang wie $\vec{a}$ und zeigt in die entgegengesetzte Richtung wie $\vec{a}$.
- $(0.5) \cdot \vec{a} = \left( \begin{array}{c} 1 \\ -1.5 \end{array} \right) \rightarrow$ Der Vektor $0.5\cdot \vec{a}$ ist halb so lang wie $\vec{a}$ und zeigt in dieselbe Richtung wie $\vec{a}$.
Hilfe zum Applet: Gib in die Eingabezeile den Buchstaben des Vektors bzw. die entsprechende Summe / Differenz an (z. B. $u=a$).
Wie Vektoren zueinander stehen
Vektoren können unterschiedliche Richtungen haben, aber auch parallel zueinander oder gar identisch sein. Optisch lässt sich das oft sehr leicht erkennen. Die Lage von Vektoren zueinander kann aber auch rechnerisch überprüft werden.
|
Unter einem Vektor versteht man die Menge aller gleich langen, gleich gerichteten und gleich orientierten Pfeile.
Der Start- bzw. Endpunkt spielen dabei keine Rolle! |
|
$2$ Vektoren stehen parallel zueinander, wenn ein Vektor als Vielfaches des anderen Vektors angeschrieben werden kann. Man sagt auch: Die Vektoren sind linear abhängig. |
Sehen wir uns die verschiedenen Fälle an:
| ident: gleiche Richtung, gleiche Orientierung, gleiche Länge |
$\vec{v} = \vec{u} \Rightarrow \vec{v} \parallel \vec{u}$ | z. B. $\vec{v}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)$ und $\vec{u}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)$ | |
| parallel (gleiche Orientierung): gleiche Richtung, gleiche Orientierung, unterschiedliche Länge |
$\exists k>0 : k \cdot \vec{v} = \vec{u} \ \ \Rightarrow \vec{v} \parallel \vec{u}$ | z. B. $\vec{v}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)$ und $\vec{u}=\left( \begin{array}{c} \frac{4}{3} \\ 2 \end{array} \right)$, $k = \frac{2}{3} $ | |
| parallel (unterschiedliche Orientierung): |
$\exists k<0 : k \cdot \vec{v} = \vec{u} \ \ \Rightarrow \vec{v} \parallel \vec{u}$ | z. B. $\vec{v}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)$ und $\vec{u}=\left( \begin{array}{c} -2 \\ -3 \end{array} \right)$, $k=-1$ | |
| linear unabhängig | $\nexists k : k \cdot \vec{v} = \vec{u} \ \ \Rightarrow \vec{v} \nparallel \vec{u}$ | z. B. $\vec{v}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)$ und $\vec{u}=\left( \begin{array}{c} 1 \\ 3 \end{array} \right)$ |
Überprüfe ob die Vektoren $\vec{a}=\left( \begin{array}{c} 2 \\ 5 \end{array} \right)$ und $\vec{b}=\left( \begin{array}{c} 4 \\ 3 \end{array} \right)$ linear unabhängig voneinander sind.
Es gibt mehrere Lösungsmöglichkeiten:
- Möglichkeit 1: Lineares Gleichungssystem mit zwei Variablen
$I: 2k = 4 \ \ \rightarrow k=2$
$II: 5k = 3 \ \ \rightarrow k=\frac{3}{5}$
Aus der ersten Gleichung ergibt sich $k=2$, in der zweiten aber $k=\frac{3}{5}$. $k$ kann aber nicht beides sein, somit haben wir eine falsche Aussage erhalten. Daraus folgt, dass die beiden Vektoren linear unabhängig und somit nicht parallel zueinander sind.
- Möglichkeit 2: „Vergleichen und Probieren“
Vergleicht man die $x$-Koordinaten der beiden Vektoren, so sieht man, dass $4$ doppelt so groß ist wie $2$. Daraus ergibt sich, dass ein etwaiges $k=2$ sein müsste. Probiert man, auch die zweite Zeile mit $2$ zu multiplizieren, so erhält man $10$. Die $y$-Koordinate von $\vec{b}$ müsste also $10$ sein, damit die beiden Vektoren parallel zueinander sind.
Betrag und Einheitsvektor
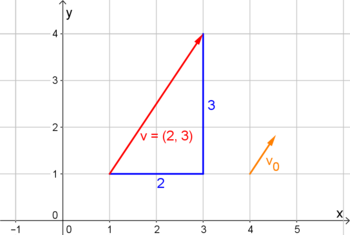
Wie anfangs bereits erwähnt, besitzen Vektoren eine Länge, auch Betrag eines Vektors genannt. Dieser wird mit Hilfe des pythagoreischen Lehrsatzes wie folgt berechnet:Sehen wir uns die Grafik rechts an, können wir mit dieser Formel die Länge des zweidimensionalen Vektors $\parallel \vec{v} \parallel$ berechnen:
Der Einheitsvektor $\vec{a_0}$ eines Vektors $\vec{a}$ ist ein zu $\vec{a}$ paralleler Vektor mit Länge $1$. Rechnerisch erhält man $\vec{a_0}$, indem man $\vec{a}$ durch seine Länge dividiert. $ \vec{a_0}
=\frac{\vec{a}}{\parallel \vec{a}\parallel}$
bzw.
$ \vec{a_0}=\frac{1}{\parallel\vec{a}\parallel}\cdot \vec{a}$
Daraus ergibt sich ein Vektor, der dieselbe Richtung des ursprünglichen Vektors hat, allerdings die Länge $1$ besitzt.
|
Sei $\vec{v} = \left( \begin{array}{c} x_1 \\ x_2 \\ ... \\ x_n \end{array} \right)$ ein Vektor der Dimension $n$ und $\parallel \vec{v} \parallel$ sein Betrag, dann ist $\vec{v_0} = \frac{1}{\parallel \vec{v} \parallel} \cdot \vec{v} \ $ der Einheitsvektor zu $\vec{v}$. |
In unserem Beispiel würde das folgendes bedeuten:
Bestimme den Einheitsvektor von $\vec{v}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)$
Vektoren bestimmter Länge
Da wir nun gelernt haben, Einheitsvektoren zu bilden und Vektoren mit Zahlen zu multiplizieren, könnt ihr euch vielleicht schon vorstellen, wie man aus einem beliebigen Vektor einen Vektor derselben Richtung, allerdings unterschiedlicher Länge bekommt. Wir haben also einen Vektor $\vec{v}=\left( \begin{array}{c} x \\ y \end{array} \right)$ mit der Länge $\parallel \vec{v} \parallel = k$ gegeben und hätten gerne den Vektor $\vec{w} \ \parallel \ \vec{v}$ mit der Länge $l$. Dazu berechnen wir zuerst den Einheitsvektor $\vec{v_0}$ von $\vec{v}$ und multiplizieren diesen dann mit $l$. So erhalten wir schließlich $\vec{w} = l \cdot \frac{\vec{v}}{k} = l \cdot \vec{v_0}$.
Mittelpunkt einer Strecke
Willst du den Mittelpunkt zwischen $2$ Punkten $A$ und $B$ berechnen, musst du wie folgt vorgehen:Zuerst berechnest du einen Vektor zwischen den Punkten ($\vec{AB}$ oder $\vec{BA}$). Dann halbierst du diesen Vektor, und erhältst $\vec{AM}$ bzw. $\vec{BM}$. Addierst du dann diesen Vektor zum entsprechenden Punkt ($A$ bzw. $B$), so erhältst du den Mittelpunkt. Also:
Dies lässt sich folgendermaßen weiter vereinfachen: $$\vec{M} = \vec{A} + \frac{\vec{AB}}{2} = \frac{2\vec{A}}{2} + \frac{\vec{B} - \vec{A}}{2} = \frac{\vec{A} + \vec{B}}{2}$$
Inhaltsverzeichnis
Dieser Artikel befasst sich mit der Vektorrechnung im zweidimensionalen Raum. Grundlegende Informationen zur Vektorrechnung, so wie Punkte und Vektoren, findest du unter dem Tab Grundlagen der Vektorrechnung.
Vektoren
Normalvektoren
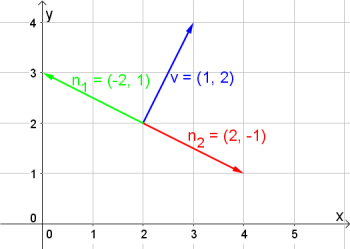
Normalvektoren zu einem Vektor sind alle Vektoren, die normal (im rechten Winkel) auf den Vektor stehen. Im $\mathbb{R^2}$ gibt es zu jedem Vektor genau $2$ Normalvektoren, die dieselbe Länge wie der ursprüngliche Vektor haben. Alle anderen Normalvektoren sind Vielfache eines dieser $2$ Normalvektoren.
|
Sei $\vec{v}=\left( \begin{array}{c} x \\ y \end{array} \right)$ ein Vektor, dann ist $\vec{n_1}=\left( \begin{array}{c} -y \\ x \end{array} \right)$ sein nach links gekippter, und $\vec{n_2}=\left( \begin{array}{c} y \\ -x \end{array} \right)$ sein nach rechts gekippter Normalvektor.
Vertausche die Koordinaten und ändere ein Vorzeichen. |
Skalarprodukt
Unter dem Skalarprodukt versteht man die Multiplikation zweier Vektoren, bei der als Ergebnis ein Skalar (eine Zahl) entsteht.
|
Seien $\vec{a}=\left( \begin{array}{c} x_a \\ y_a \end{array} \right)$ und $\vec{b}=\left( \begin{array}{c} x_b \\ y_b \end{array} \right)$ zwei Vektoren, dann ist $\vec{a} \cdot \vec{b} = \left( \begin{array}{c} x_a \\ y_a \end{array} \right) \cdot \left( \begin{array}{c} x_b \\ y_b \end{array} \right) = x_a \cdot x_b + y_a \cdot y_b$ gleich ihr Skalarprodukt. |
Das Skalarprodukt wirkt auf den ersten Blick etwas „eigenartig“. Man kann sich die Bedeutung des Skalarproduktes besonders gut an einem Anwendungsbeispiel erklären:
Angenommen in einer Preisliste stehen $10$ Kugelschreiber, die jeweils $2€$ kosten und $20$ Bleistifte, die jeweils $0.50€$ kosten.
In Tabellenform sieht das folgendermaßen aus:
| Produkt | Stückzahl | Preis pro Stück (in $€$) |
|---|---|---|
| Kugelschreiber | $10$ | $2$ |
| Bleistift | $20$ | $0.50$ |
Aus dieser Tabelle kann ein Stückzahlvektor $\left( \begin{array}{c} 10 \\ 20 \end{array} \right)$ und ein Preisvektor $\left( \begin{array}{c} 2 \\ 0.50 \end{array} \right)$ abgelesen werden.
Möchte man den Gesamtwert der Produkte berechnen, so müssen jeweils die Einzelpreise mit der Stückzahl multipliziert und anschließend die Summe gebildet werden.
Genau das macht das Skalarprodukt:
$\left( \begin{array}{c} 10 \\ 20\end{array} \right) \cdot \left( \begin{array}{c} 2 \\ 0.50 \end{array} \right) = 10 \cdot 2 + 20 \cdot 0.50 = 20 + 10 = 30€ $
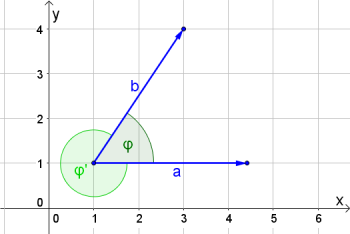
Winkel zwischen zwei Vektoren
$$cos{\varphi} = \frac{\vec{a} \cdot \vec{b} }{\parallel \vec{a} \parallel \cdot \parallel \vec{b} \parallel} = \vec{a_0} \cdot \vec{b_0}$$bzw. $$\vec{a} \cdot \vec{b} = \parallel \vec{a} \parallel \cdot \parallel \vec{b} \parallel \cdot cos{\varphi}$$
Heißt es, den Winkel zwischen $2$ Vektoren/Geraden zu bestimmen, ist damit immer der kleinere Winkel gemeint. Solltest du einmal ein Ergebnis erhalten, das größer als $180°$ ist (nennen wir dieses Ergebnis $\varphi'$), dann ziehe dieses Ergebnis von $360°$ ab und du erhältst den kleineren Winkel ($\varphi = 360° - \varphi'$).
Bei einem Winkel von $\varphi = 90°$ erhalten wir $cos{\varphi} = 0$, was bedeutet, dass auch $\vec{a} \cdot \vec{b} = 0$. Daraus ergibt sich das Orthogonalitätskriterium.
Orthogonalitätskriterium
|
Ergibt das Skalarprodukt zweier Vektoren $0$, so stehen diese zwei Vektoren normal zueinander (und umgekehrt). $$\vec{a} \cdot \vec{b} \ = \ 0 \ \Leftrightarrow \ \vec{a} \bot \vec{b}$$ |
Mithilfe des Orthogonalitätskriteriums kann man auch zeigen, dass $\vec{n}=\left( \begin{array}{c} y \\ -x \end{array} \right)$ stets ein Normalvektor von $\vec{v}=\left( \begin{array}{c} x \\ y \end{array} \right)$ ist.
$$\vec{v} \cdot \vec{n} = \left( \begin{array}{c} x \\ y \end{array} \right) \cdot \left( \begin{array}{c} y \\ -x \end{array} \right) = xy - yx = 0$$
| Übungsaufgabe |
|---|
Geraden
Darstellungsformen
Geraden lassen sich in unterschiedlichen Formen darstellen. In der Vektorrechnung ist die Parameterdarstellung populär, da man dazu nur einen Punkt und einen Vektor kennen muss. Die Normalform allerdings hat den Vorteil, dass man den Normalvektor zur Geraden auf einen Blick ablesen kann. Je nachdem, was man mit der Gerade vorhat, können die verschiedenen Formen ineinander umgewandelt werden.
Parameterdarstellung
$$g: \vec{0X} = \vec{0P} + t \cdot \vec{a}$$wobei
- $X \in g$ ist ein beliebiger Punkt auf der unendlichen Geraden (steht für alle Punkte auf der Geraden)
- $P \in g$ ist ein bekannter Punkt auf der Geraden
- $t \in \mathbb{R}$ ist ein freier Parameter (in der Grafik rechts $\lambda$)
- $\vec{a} \in \mathbb{R^2}$ ist ein Vektor parallel zur Geraden, der die Richtung dieser angibt („Richtungsvektor“)
Beachte, dass in der Parameterdarstellung keine Punkte, sondern Ortsvektoren verwendet werden. (Genauere Informationen zu Ortsvektoren findest du unter Grundlagen der Vektorrechnung.)
Wenn man das weiß, kann man der Einfachheit halber die Gerade auch folgendermaßen beschreiben: $g: X = P + t \cdot \vec{a}$
Eine andere Schreibweise ist, die Koordinaten einzeln zu betrachten und $2$ Gleichungen aufzustellen:
$$g : \begin{cases} x = x_P + t \cdot x_a \\ y = y_P + t \cdot y_a \end{cases}$$
Normalvektorform
Hierzu benötigt man einen Normalvektor des Richtungsvektors und multipliziert dann die Geradengleichung mit diesem Normalvektor. Da $\vec{a} \cdot \vec{n} = 0$, bleibt über:
Sei $g: \vec{0X} = \vec{0P} + t \cdot \vec{a}$ eine Gerade in Parameterform, so ist
dieselbe Gerade in Normalform, wobei $\vec{0X}=\left( \begin{array}{c} x \\ y \end{array} \right), \ \vec{0P}=\left( \begin{array}{c} x_P \\ y_P \end{array} \right), \ \vec{a}=\left( \begin{array}{c} x_a \\ y_a \end{array} \right)$ und $\vec{n}=\left( \begin{array}{c} y_a \\ -x_a \end{array} \right)$ ein Normalvektor von $\vec{a}$ (hier kann man natürlich auch den anderen Normalvektor verwenden).
Allgemeine Geradengleichung
Diese Form der Darstellung heißt auch Normalform, da man den Normalvektor der Geraden direkt ablesen kann. Um von der Parameterdarstellung auf diese Form zu kommen, gibt es $2$ Möglichkeiten:
1. Multiplikation mit Normalvektor: Hierzu muss man einfach die Normalform ausmultiplizieren und es ergibt sich:
$$g: y_a \cdot x + -x_a \cdot y = y_a \cdot x_P + -x_a \cdot y_P$$
2. Elimination des Parameters:
Hierbei gehen wir von der Geradenform $g : \begin{cases} x = x_P + t \cdot x_a \\ y = y_P + t \cdot y_a \end{cases}$ aus, eliminieren $t$, und kommen ebenfalls auf die obige allgemeine Geradengleichung.
Auf der rechten Seite der Gleichung stehen nur bekannte Größen, auf der linken Seiten stehen Vielfache von $x$ und $y$. Diese Gleichung kann man weiter auch auf die Form $y=kx+d$ umformen.
Lagebeziehungen zwischen Geraden
Mehrere Geraden können im $\mathbb{R^2}$
- ident sein, d. h. sie haben unendlich viele gemeinsame Punkte.
- parallel sein, d. h. sie haben keinen gemeinsamen Punkt.
- einander schneiden, d. h. sie haben genau einen gemeinsamen Punkt (Schnittpunkt).
Sind $2$ Geraden in Parameterdarstellung gegeben, betrachten wir zuerst ihre Richtungsvektoren.
Sind diese parallel zueinander, so sind auch die Geraden parallel zueinander. Nun bleibt noch die Frage offen, ob die Geraden ident sind. Dazu überprüfen wir einfach, ob der gegebene Punkt der einen Geraden auch auf der anderen Geraden liegt. Dazu setzen wir den bekannten Punkt der einen Geraden für den unbekannten Punkt der anderen Geraden ein und erhalten $2$ Gleichungen in einer Unbekannten (Parameter der zweiten Gerade). Erhalten wir nun für den Parameter zweimal dasselbe Ergebnis, so sind die $2$ Geraden ident, erhalten wir unterschiedliche Ergebnisse, so sind sie nur parallel.
Sind die Richtungsvektoren nicht parallel zueinander, so sind es auch die $2$ Geraden nicht, und wir können uns sicher sein, dass diese einen gemeinsamen Schnittpunkt besitzen. Doch wie erhalten wir den Schnittpunkt? Ganz einfach, indem wir die $2$ Geraden schneiden. Dazu müssen wir sie gleichsetzen und dann das dadurch erhaltene Gleichungssystem in $2$ Unbekannten (die $2$ Parameter) lösen. Wenn wir den Wert eines Parameters ausgerechnet haben, setzen wir ihn einfach in die entsprechende Geradengleichung ein und erhalten so den Schnittpunkt.
Gegeben sind die beiden Geraden $g: X = \left( \begin{array}{c} -3 \\ 1 \end{array} \right) + s \cdot \left( \begin{array}{c} 4 \\ -2 \end{array} \right)$ und $h: X = \left( \begin{array}{c} 0 \\ 2 \end{array} \right) + t \cdot \left( \begin{array}{c} -2 \\ 1 \end{array} \right)$. Ermittle deren gegenseitige Lage und ggf. deren Schnittpunkt!
$$\left( \begin{array}{c} 4 \\ -2 \end{array} \right) = -2 \cdot \left( \begin{array}{c} -2 \\ 1 \end{array} \right) \ \Rightarrow \ g \parallel h$$ Nun überprüfen wir, ob der Punkt der Geraden $h$ auf $g$ liegt: $$\left( \begin{array}{c} 0 \\ 2 \end{array} \right) = \left( \begin{array}{c} -3 \\ 1 \end{array} \right) + s \cdot \left( \begin{array}{c} 4 \\ -2 \end{array} \right) \ \rightarrow \ \begin{cases} 0 = -3 + 4s \ \rightarrow \ s_1 = \frac{3}{4} \\ 2 = 1 - 2s \ \rightarrow \ s_2 = -\frac{1}{2} \end{cases} \ \rightarrow \ s_1 \neq s_2 \ \Rightarrow \ g \not\equiv h$$
Gegeben sind die beiden Geraden $g: X = \left( \begin{array}{c} -3 \\ 1 \end{array} \right) + s \cdot \left( \begin{array}{c} 2 \\ -1 \end{array} \right)$ und $h: X = \left( \begin{array}{c} 0 \\ 2 \end{array} \right) + t \cdot \left( \begin{array}{c} 1 \\ 2 \end{array} \right)$. Ermittle deren gegenseitige Lage und ggf. deren Schnittpunkt!
$$\begin{align} I: \ &-3&+&2s&=&0&+&t \\ II: \ &1&-&s&=&2&+&2t \end{align}$$ $$I + 2 \cdot II: \ -1 = 4 + 5t \ \rightarrow \ t = -1$$ $$t \ in \ h: S = \left( \begin{array}{c} 0 \\ 2 \end{array} \right) + (-1) \cdot \left( \begin{array}{c} 1 \\ 2 \end{array} \right) = \left( \begin{array}{c} -1 \\ 0 \end{array} \right)$$
Sind die $2$ Geraden in der allgemeinen Geradenform gegeben, so haben wir bereits $2$ Gleichungen, die wir nach $x$ und $y$ auflösen. Dieses $x$ und $y$ sind die Koordinaten des Schnittpunktes. Sollte sich keine Lösung ergeben, so schneiden sich die Geraden nicht.
Um das Schneiden von Geraden besser zu verstehen, schau dir das Lösen von Gleichungssystemen genauer an, wirf einen Blick auf die Beispiele zum $\mathbb{R^2}$ unter dem Tab 'Beispiele', oder sieh dir dieses Video an:
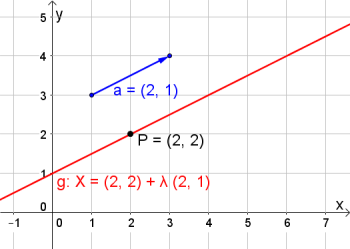
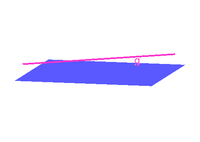
Normalabstand Punkt - Gerade
Gegeben sei ein Punkt $Q(x_Q|y_Q)$ und eine Gerade $g: X = P + t \cdot \vec{a}$. Um den Normalabstand $d(Q,g)$ zwischen $Q$ und $g$ zu berechnen, gehe wie folgt vor:
|
1. Bestimme die Gerade $q: X = Q + s \cdot \vec{n}$, die durch $Q$ geht und den Normalvektor $\vec{n}$ von $\vec{a}$ als Richtungsvektor besitzt.
2. Schneide $g$ und $q$ und du erhältst deren Schnittpunkt $S$. |
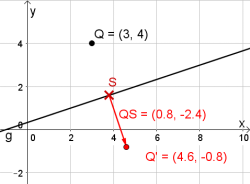
In der Grafik rechts hätten wir z. B. die Angabe $g: X = \left( \begin{array}{c} 2 \\ 1 \end{array} \right) + \lambda \cdot \left( \begin{array}{c} 3 \\ 1 \end{array} \right)$ und $Q(3|4)$. Du kannst das zur Übung durchrechnen.
Hesse'sche Abstandsformel
Mithilfe dieser Formel kann man ebenfalls den Abstand $d(Q,g)$ zwischen Punkt $Q(x_Q|y_Q)$ und Gerade $g: X = P + t \cdot \vec{a}$ bestimmen. $$d(Q,g) = | \vec{PQ} \cdot \vec{n_0} |$$ wobei $\vec{n_0}$ der normierte (Länge $1$) Normalvektor des Richtungsvektors $\vec{a}$ der Geraden $g$ ist.
Spiegelung eines Punktes an einer Geraden
Gegeben sei ein Punkt $Q(x_Q|y_Q)$ und eine Gerade $g: X = P + t \cdot \vec{a}$. Es gilt den Punkt $Q$ an der Gerade $g$ zu spiegeln, und so den Punkt $Q'$ zu erhalten. Dazu befolgst du die Vorgehensweise von "Normalabstand Punkt - Gerade" bis du den Vektor $\vec{QS}$ erhältst und trägst diesen vom Punkt $S$ ab, also:$$Q' = S + \vec{QS}$$
Inhaltsverzeichnis
Vektoren
Kreuzprodukt
Im $\mathbb{R^3}$ gibt es neben dem Skalarprodukt, bei dem wir als Ergebnis ein Skalar erhalten, eine weitere Möglichkeit, zwei Vektoren miteinander zu multiplizieren: das sogenannte Kreuz- oder Vektorprodukt, bei dem wir als Ergebnis einen Vektor erhalten.
|
Seien $\vec{a}=\left( \begin{array}{c} x_a \\ y_a \\ z_a \end{array} \right)$ und $\vec{b}=\left( \begin{array}{c} x_b \\ y_b \\ z_b \end{array} \right)$ zwei Vektoren des $\mathbb{R^3}$, dann ist ihr Kreuzprodukt
$$\vec{a} \times \vec{b} = \left( \begin{array}{c} x_a \\ y_a \\ z_a \end{array} \right) \times \left( \begin{array}{c} x_b \\ y_b \\ z_b \end{array} \right) = \left( \begin{array}{c} y_a \cdot z_b - z_a \cdot y_b \\ z_a \cdot x_b - x_a \cdot z_b \\ x_a \cdot y_b - y_a \cdot x_b \end{array} \right)$$ |
Gegeben seien die Vektoren $\vec{a}=\left( \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right)$ und $\vec{b}=\left( \begin{array}{c} 5 \\ 4 \\ -3 \end{array} \right)$, gesucht ist ihr Kreuzprodukt.
Wozu wir das Kreuzprodukt überhaupt benötigen, sehen wir in den folgenden beiden Unterabschnitten.
Normalvektoren
Im $\mathbb{R^3}$ gibt es zu einem Vektor unendlich viele Normalvektoren. Auf eine Ebene allerdings gibt es genau $2$ Normalvektoren (wie im $\mathbb{R^2}$ auf eine Gerade). Eine Ebene wird von $2$ Vektoren aufgespannt, deren Kreuzprodukt ergibt einen Normalvektor $\vec{n_1}$. Dieser steht normal auf die Ebene bzw. auf die beiden Vektoren. Der zweite Normalvektor hat die entgegengesetzte Orientierung ($\vec{n_2} = -\vec{n_1}$). Man schreibt $$\vec{n} = \vec{a} \times \vec{b}$$
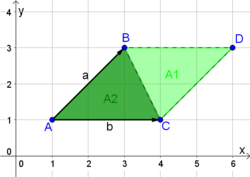
Fläche eines von zwei Vektoren aufgespannten Parallelogramms oder Dreiecks
|
Die Länge $\parallel \vec{n} \parallel = \parallel \vec{a} \times \vec{b} \parallel$ des Normalvektors $\vec{n}$ zu den Vektoren $\vec{a}$ und $\vec{b}$ entspricht der Maßzahl des Flächeninhaltes des Parallelogramms, das $\vec{a}$ und $\vec{b}$ aufspannen (im Bild die gesamte grüne Fläche).
Die Hälfte dieser Fläche entspricht der Fläche des aufgespannten Dreiecks. |
Skalarprodukt, Orthogonalitätskriterium, Winkel zwischen zwei Vektoren
Das Skalarprodukt, Orthogonalitätskriterium und Winkelmaß für Vektoren in $\mathbb{R^3}$ ist analog definiert wie in $\mathbb{R^2}$. Wir wiederholen nochmals kurz:
Skalarprodukt
Seien $\vec{a}=\left( \begin{array}{c} x_a \\ y_a \\ z_a \end{array} \right)$ und $\vec{b}=\left( \begin{array}{c} x_b \\ y_b \\z_b \end{array} \right)$ zwei Vektoren, dann ist $$\vec{a} \cdot \vec{b} = \left( \begin{array}{c} x_a \\ y_a \\ z_a \end{array} \right) \cdot \left( \begin{array}{c} x_b \\ y_b \\ z_b \end{array} \right) = x_a \cdot x_b + y_a \cdot y_b + z_a \cdot z_b$$ gleich ihr Skalarprodukt.
| Übungsaufgabe |
|---|
Orthogonalitätskriterium
Ergibt das Skalarprodukt zweier Vektoren $0$, so stehen diese zwei Vektoren normal zueinander (und umgekehrt).
$$\vec{a} \cdot \vec{b} \ = \ 0 \ \Leftrightarrow \ \vec{a} \bot \vec{b}$$
Winkel zwischen zwei Vektoren
$$cos{\varphi} = \frac{\vec{a} \cdot \vec{b} }{\parallel \vec{a} \parallel \cdot \parallel \vec{b} \parallel} = \vec{a_0} \cdot \vec{b_0}$$
Geraden
Darstellungsformen
Parameterdarstellung
Die Parameterdarstellung im $\mathbb{R^3}$ sieht genauso aus wie im $\mathbb{R^2}$, einziger Unterschied ist, dass unsere Punkte und Vektoren hier jeweils $3$ Koordinaten haben.$$g: X = P + t \cdot \vec{a}$$ bzw. $$g : \begin{cases} x = x_P + t \cdot x_a \\ y = y_P + t \cdot y_a \\ z = z_P + t \cdot z_a \end{cases}$$ Mehr Infos zu den einzelnen Komponenten findest du unter dem Tab 'Im $\mathbb{R^2}$'.
Parameterfreie Darstellungsform
Diese besteht aus $2$ Gleichungen und wir erhalten sie durch Eliminierung des Parameters.
Gegeben sei die Parameterform der Gerade $g: X = \left( \begin{array}{c} 2 \\ 0 \\ 1 \end{array} \right) + t \cdot \left( \begin{array}{c} 3 \\ -4 \\ 1 \end{array} \right)$. Zuerst schreiben wir das in die $3$ Koordinatengleichungen um:
$$g : \begin{cases} x = 2 + 3t \\ y = 0 - 4t \\ z = 1 + t \end{cases}$$
Anschließend multiplizieren wir die dritte Gleichung mit $3$ und subtrahieren diese von der ersten Gleichung: $$- \begin{cases} x = 2 + 3t \\ 3z = 3 + 3t \end{cases}$$ So erhalten wir die Gleichung $x - 3z = -1$. Die parameterfreie Darstellung unserer Geraden lautet somit $$g : \begin{cases} 4x + 3y = 8 \\ x - 3z = -1 \end{cases}$$
Die zwei Gleichungen in der parameterfreien Darstellung sind übrigens Ebenengleichungen. Die eigentliche Gerade ist der Schnitt dieser zwei Ebenen.
Lagebeziehungen zwischen Geraden
Mehrere Geraden können im $\mathbb{R^3}$
- ident sein, d. h. sie haben unendlich viele gemeinsame Punkte.
- parallel sein, d. h. sie haben keinen gemeinsamen Punkt.
- einander schneiden, d. h. sie haben genau einen gemeinsamen Punkt (Schnittpunkt).
- windschief sein, d. h. sie haben keinen gemeinsamen Punkt und sind nicht parallel.
Um herauszufinden, wie $2$ gegebene Geraden in Parameterform zueinander stehen, gehst du am besten wie folgt vor:
Betrachtung der Richtungsvektoren: Auch im $\mathbb{R^3}$ gilt, sind die Richtungsvektoren zweier Geraden parallel zueinander (d. h. man kann einen Vektor als Vielfaches des anderen Vektors darstellen), so sind es auch die Geraden.
Fall 1: Die Vektoren sind parallel: Sollte sich herausstellen, dass die zwei Geraden parallel zueinander sind, überprüfst du als nächstes, ob sie einen gemeinsamen Punkt haben; am einfachsten funktioniert das, indem du den bekannten Punkt ($P$) der einen Geraden in die zweite Gerade (für den unbekannten Punkt $X$) einsetzt. Wir erhalten drei Gleichungen in einer Unbekannten (Parameter der zweiten Gerade).
Fall 1a: Erhalten wir nun für den Parameter dreimal dasselbe Ergebnis, so sind die $2$ Geraden ident (und parallel), da der überprüfte Punkt, und somit unendlich weitere, auf beiden Geraden liegen.
Fall 1b: Erhalten wir unterschiedliche Ergebnisse, so sind sie nur parallel, da der überprüfte Punkt, und somit auch kein anderer, nicht auf beiden Geraden liegt.
Fall 2: Die Vektoren sind nicht parallel: Nun gibt es nur noch zwei Möglichkeiten: Entweder die zwei Geraden haben einen gemeinsamen Punkt (Schnittpunkt), oder sie sind windschief.
Um das wiederum herauszufinden, setzt du die beiden Geraden gleich, d. h. du stellst ein lineares Gleichungssystem (LGS) mit drei Gleichungen und in drei Unbekannten auf, und versuchst, dieses zu lösen.
Fall 2a: Solltest du nun eine Lösung erhalten, d. h. du erhältst den Wert für den Parameter einer der zwei Geraden (und hast diesen Wert überprüft), so weißt du, dass die zwei Geraden einander schneiden. Den Schnittpunkt erhältst du jetzt, indem du den erhaltenen Wert für den Parameter in die entsprechende Geradengleichung einsetzt.
Fall 2b: Sollte dein LGS keine Lösung ergeben (also sich eine falsche Aussage oder ein Widerspruch ergeben, z. B. $2=13$, oder $t=4$ und $t=-1$), dann weißt du, dass deine beiden Geraden keinen Schnittpunkt haben und somit windschief sind.
Zum besseren Verständnis siehst du dir am besten das folgende Video und die beiden folgenden Beispiele an.
Gegeben sind die beiden Geraden $g: X = \left( \begin{array}{c} 0 \\ -11 \\ -3 \end{array} \right) + s \cdot \left( \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right)$ und $h: X = \left( \begin{array}{c} 2 \\ 3 \\ -3 \end{array} \right) + t \cdot \left( \begin{array}{c} 1 \\ -3 \\ 2 \end{array} \right)$. Überprüfe deren gegenseitige Lage und gegebenenfalls ihren Schnittpunkt!
$g$ und $h$ sind also nicht parallel. Sie können also entweder einander schneiden oder windschief sein. Stellen wir nun ein LGS auf, indem wir die beiden Geraden gleichsetzen:
$$\begin{align}
I: \ &&&s&=&2&+&t \\
II: \ &-11&+&2s&=&3&-&3t \\
III: \ &-3&+&s&=&-3&+&2t
\end{align}$$
Wir subtrahieren $III$ von $I$: $- \begin{cases} &s &=& 2 + t \\ -3 + &s &=& -3 + 2t \end{cases} \ \rightarrow \ 3 = 5 - t \Rightarrow t = 2$
Wir überprüfen dieses Ergebnis für $t$, indem wir $t=2$ in alle $3$ Gleichungen einsetzen. Wir sehen dann, dass wir überall dasselbe Ergebnis für $s$ erhalten, nämlich $s=4$. Daraus folgt, dass die Geraden einander schneiden. Setzen wir nun $t=2$ oder $s=4$ in die entsprechende Geradengleichung ein, so erhalten wir den Schnittpunkt $S(4\vert -3\vert 1)$ der beiden Geraden.
Gegeben sind die beiden Geraden $g: X = \left( \begin{array}{c} 3 \\ -2 \\ 0 \end{array} \right) + s \cdot \left( \begin{array}{c} 2 \\ -2 \\ 1 \end{array} \right)$ und $h: X = \left( \begin{array}{c} 4 \\ 3 \\ 1 \end{array} \right) + t \cdot \left( \begin{array}{c} -1 \\ 0 \\ 1 \end{array} \right)$. Überprüfe deren gegenseitige Lage und ggf. ihren Schnittpunkt!
Nun stellen wir wieder ein LGS auf:
$$\begin{align}
I: \ &3&+&2s&=&4&-&t \\
II: \ &-2&-&2s&=&3&& \\
III: \ &&&s&=&1&+&t
\end{align}$$
Aus der zweiten Gleichung lässt sich direkt berechnen, dass $s=- \frac{5}{2}$. Dies setzen wir nun in die erste und zweite Gleichung ein und erhalten einmal $3 - 5 = 4 - t \ \Rightarrow \ t=6$ und einmal $- \frac{5}{2} = 1 + t \ \Rightarrow \ t=- \frac{7}{2}$. Diese beiden Werte für $t$ sind offensichtlich voneinander unterschiedlich, daraus folgt, dass die beiden Geraden $g$ und $h$ windschief sind.
Ebenen
Eine Ebene ist durch $3$ Punkte oder $1$ Punkt und $2$ (voneinander linear unabhängigen) Vektoren eindeutig festgelegt.
Darstellungsformen
Parameterdarstellung
$$\epsilon : X = P + s \cdot \vec{a} + t \cdot \vec{b}$$ bzw. $$\epsilon : \begin{cases} x = x_P + s \cdot x_a + t \cdot x_b \\ y = y_P + s \cdot y_a + t \cdot y_b \\ z = z_P + s \cdot z_a + t \cdot z_b \end{cases}$$ wobei
- $X \in \epsilon$ ist ein beliebiger Punkt auf der unendlichen Ebene
- $P \in \epsilon$ ist ein bekannter Punkt auf der Ebene
- $s, t \in \mathbb{R}$ sind freie Parameter
- $\vec{a}, \vec{b} \in \mathbb{R^3}$ sind zwei Vektoren, die parallel zur Ebene liegen
Normalvektorform
Man multipliziert die Parameterdarstellung der Ebene mit ihrem Normalvektor $\vec{n} = \vec{a} \times \vec{b}$ und erhält$$\vec{n} \cdot \vec{X} = \vec{n} \cdot \vec{P}$$
Allgemeine Ebenengleichung
$$ax + by + cz = d$$Diese Form der Darstellung heißt auch Normalform, da man den Normalvektor der Ebene direkt ablesen kann. Um von der Parameterdarstellung auf diese Form zu kommen, gibt es $2$ Möglichkeiten:
1. Multiplikation mit Normalvektor: Hierzu muss man einfach die Normalform ausmultiplizieren und es ergibt sich:
$$\epsilon: x_n \cdot x + y_n \cdot y + z_n \cdot z = x_n \cdot x_P + y_n \cdot y_P + z_n \cdot z_P$$
2. Elimination des Parameters:
Hierbei gehen wir von der Ebenengleichung $\epsilon : \begin{cases} x = x_P + s \cdot x_a + t \cdot x_b \\ y = y_P + s \cdot y_a + t \cdot y_b \\ z = z_P + s \cdot z_a + t \cdot z_b \end{cases}$ aus, eliminieren $s$ und $t$, und kommen ebenfalls auf die obige allgemeine Ebenengleichung.
Zur Veranschaulichung ein Beispiel zu den verschiedenen Darstellungsformen:
Gegeben seien die drei Punkte $A(1 \vert 1 \vert 1), B(-1 \vert -4 \vert 2), C(0 \vert 3 \vert -1)$. Gib die Ebene, die diese drei Punkte aufspannen, in Parameterform, Normalform und allgemeiner Ebenengleichung an!
$$\epsilon: X = \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) + s \cdot \left( \begin{array}{c} -2 \\ -5 \\ 1 \end{array} \right) + t \cdot \left( \begin{array}{c} 1 \\ 2 \\ -2 \end{array} \right)$$
Um auf die Normalform zu kommen, bestimmen wir als erstes den Normalvektor der Ebenen: $\vec{n} = \vec{AB} \times \vec{AC} = \left( \begin{array}{c} -2 \\ -5 \\ 1 \end{array} \right) \times \left( \begin{array}{c} -1 \\ 2 \\ -2 \end{array} \right) = \left( \begin{array}{c} (-5) \cdot (-2) - 1 \cdot 2 \\ 1 \cdot (-1) - (-2) \cdot (-2) \\ (-2) \cdot 2 - (-5) \cdot (-1) \end{array} \right) = \left( \begin{array}{c} 8 \\ -5 \\ -9 \end{array} \right)$.
Nun die Parametergleichung mit dem Normalvektor multiplizieren und wir erhalten auch die Normalform:
$$\epsilon: \left( \begin{array}{c} 8 \\ -5 \\ -9 \end{array} \right) \cdot \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} 8 \\ -5 \\ -9 \end{array} \right) \cdot \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right)$$
Um nun noch die allgemeine Ebenenform zu erhalten, multipliziert man am einfachsten die Normalform aus und erhält:
$$\epsilon: 8x - 5y -9z =-6$$
Aber auch die Elimination der Parameter soll hier gezeigt werden. Wir gehen aus von: $$\epsilon : \begin{cases} x = 1 - 2s - t \\ y = 1 - 5s + 2t \\ z = 1 + s - 2t\end{cases}$$
Addieren wir die $y$- und die $z$-Gleichung, können wir $t$ eliminieren: $+ \begin{cases} y = 1 - 5s + 2t \\ z = 1 + s - 2t \end{cases} \ \Rightarrow \ y + z = 2 - 4s$.
Wir können $t$ ebenfalls eliminieren, indem wir die $y$-Gleichung zum $2$-fachen der $x$-Gleichung addieren: $+ \begin{cases} 2x = 2 - 4s - 2t \\ y = 1 - 5s + 2t \end{cases} \ \Rightarrow \ 2x + y = 3 -9s$.
Nun haben wir zwei Gleichungen, die nur mehr von $s$ abhängig sind. Um diesen Parameter nun auch noch zu eliminieren, multiplizieren wir die erste Gleichung mit $(-9)$ und die zweite mit $4$ und addieren diese, um nochmals auf die allgemeine Ebenengleichung zu kommen.
$$+ \begin{cases} 8x + 4y = 12 - 36s \\ -9y - 9z = -18 + 36s \end{cases} \ \Rightarrow \ \epsilon: 8x - 5y -9z =-6$$
Lagebeziehungen
...zwischen zwei Ebenen
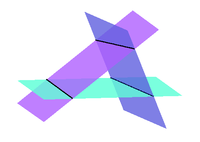
Zwei Ebenen können im $\mathbb{R^3}$
- ident sein: die Ebenengleichungen (allg. Form) sind Vielfache voneinander;
z. B. $\epsilon _1 : x + y + z = 3$ und $\epsilon _2 : 2x + 2y + 2z = 6 \Rightarrow \epsilon _2 = 2 \cdot \epsilon _1$
- parallel sein: die Normalvektoren der Ebenen sind Vielfache voneinander;
z. B. $\epsilon _1 : x + y + z = 3$ und $\epsilon _2 : 2x + 2y + 2z = 5 \Rightarrow \vec{n_2} = 2 \cdot \vec{n_1}$
- einander schneiden (in einer Geraden): die Normalvektoren der Ebenen sind keine Vielfache voneinander;
z. B. $\epsilon _1 : x + y + z = 3$ und $\epsilon _2 : x - 3y + 2z = 1 \Rightarrow \nexists \lambda \in \mathbb{R} : \vec{n_1} = \lambda \cdot \vec{n_2}$
Berechnen der Schnittgeraden
Erkennt man durch Betrachtung der Normalvektoren zweier Ebenen, dass diese einander schneiden müssen, so kann man diese Schnittgerade berechnen. Dazu erstellt man aus den beiden Ebenengleichungen ein lineares Gleichungssystem in $3$ Unbekannten. $2$ Gleichungen - $3$ Unbekannte: Wir werden hier nicht für alle Unbekannten einen Zahlenwert erhalten, können aber $2$ Unbekannte in Abhängigkeit der dritten darstellen. Diese dritte Unbekannte wird uns als Parameter für die Darstellung der Geraden dienen. Zur Veranschaulichung ein Beispiel:
Gegeben seien die beiden Ebenen $\epsilon _1 : x + y + z = 3$ und $\epsilon _2 : x - 3y + 2z = 1$. Wie wir weiter oben schon festgestellt haben, müssen diese Ebenen einander schneiden, da die beiden Normalvektoren der Ebenen $\vec{n_1}=\left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right)$ und $\vec{n_2}=\left( \begin{array}{c} 1 \\ -3 \\ 2 \end{array} \right)$ linear unabhängig sind, also $\nexists \lambda \in \mathbb{R} : \vec{n_1} = \lambda \cdot \vec{n_2}$.
- Wir wählen nun eine der Koordinaten als Parameter, z. B. $z=t$ und stellen das Gleichungssystem auf.
Wir subtrahieren $I-II$ und erhalten $$4y - t = 2 \ \Rightarrow \ y = \frac{1}{2} + t \cdot \frac{1}{4}$$ Nun setzen wir unser erhaltenes $y$ in die erste Gleichung ein, um $x$ zu erhalten:
$$I: \ x + \frac{1}{2} + t \cdot \frac{1}{4} + t = 3 \ \Rightarrow \ x = \frac{5}{2} - t \cdot \frac{5}{4}$$ Somit haben wir alle Ausdrücke der Koordinaten gefunden ($z=t$ haben wir anfangs festgelegt) und können die Parameterdarstellung der Schnittgeraden angeben: $$g: X = \left( \begin{array}{c} \frac{5}{2} \\ \frac{1}{2} \\ 0 \end{array} \right) + t \cdot \left( \begin{array}{c} - \frac{5}{4} \\ \frac{1}{4} \\ 1 \end{array} \right)$$
...zwischen drei Ebenen
Drei Ebenen können im $\mathbb{R^3}$
- alle ident sein
- $2$ ident, $1$ parallel sein
- alle parallel sein
- $3$ Schnittgeraden haben
- $2$ Schnittgeraden haben ($2$ Ebenen parallel)
- $1$ Schnittgerade haben
- $1$ Schnittpunkt haben
...zwischen Ebene und Gerade
Eine Ebene und eine Gerade können im $\mathbb{R^3}$
- $g \subset \epsilon$, die Gerade liegt auf der Ebene
Hierbei haben die Gerade und die Ebene einen gemeinsamen Punkt und der Richtungsvektor der Geraden steht normal auf den Normalvektor der Ebene, daraus folgt, dass sie unendlich viele gemeinsame Punkte haben.
- parallel sein
Irgendein Punkt der Geraden liegt nicht auf der Ebene, der Richtungsvektor der Geraden steht normal auf den Normalvektor der Ebene, daraus folgt, dass sie keinen einzigen gemeinsamen Punkt haben.
- $1$ Schnittpunkt haben
Der Richtungsvektor der Geraden steht nicht normal auf den Normalvektor der Ebene.
Zur Überprüfung der Lagebeziehung gibt es allerdings noch eine andere (schnellere) Methode. Hier „schneiden“ wir die Gerade und die Ebene mathematisch, d. h. wir setzen sie gleich (wenn beide in Parameterform gegeben sind) oder setzen die Gerade $g$ (Parameterform) in die Ebene $\epsilon$ (allg. Ebenengleichung) ein.
Wir erhalten dadurch ein Gleichungssystem oder eine einzelne Gleichung.
Sei die Gerade gegeben als $g : \begin{cases} x = x_P + t \cdot x_a \\ y = y_P + t \cdot y_a \\ z = z_P + t \cdot z_a \end{cases}$ und die Ebene als $\epsilon : \begin{cases} x = x_Q + s \cdot x_b + u \cdot x_c \\ y = y_Q + s \cdot y_b + u \cdot y_c \\ z = z_Q + s \cdot z_b + u \cdot z_c \end{cases}$ (Parameterform) oder $\epsilon : ax + by + cz = d$ (allg. Ebenengleichung).
Wir erhalten als Gleichungssystem durch Gleichsetzen der Gleichungen der Parameterformen:
$$\begin{cases} x_P + t \cdot x_a = x_Q + s \cdot x_b + u \cdot x_c \\ y_P + t \cdot y_a = y_Q + s \cdot y_b + u \cdot y_c \\ z_P + t \cdot z_a = z_Q + s \cdot z_b + u \cdot z_c \end{cases}$$
Wir erhalten durch Einsetzen der Geraden in die Ebene (allg. Ebenengleichung):
$$a \cdot (x_P + t \cdot x_a) + b \cdot (y_P + t \cdot y_a) + c \cdot (z_P + t \cdot z_a) = d$$
Ergibt sich hier eine wahre Aussage (z. B. $1=1$), also unendlich viele Lösungen, so liegt die Gerade in der Ebene.
Ergibt sich eine falsche Aussage (z. B. $1=2$), also keine Lösung, so schneiden die beiden Objekte einander nicht, also sind sie parallel.
Gibt es genau eine Lösung (z. B. $t=2$), so existiert genau ein gemeinsamer Punkt $=$ Schnittpunkt. Diesen erhält man, indem man den ermittelten Wert für den Parameter $t$ der Geraden in die Geradengleichung einsetzt (oder, wenn die Ebene in Parameterform gegeben war, die beiden Werte für die Parameter $s$ und $u$ der Ebene in die Ebenengleichung einsetzt). Dazu $2$ Beispiele, wobei wir im ersten mit der Ebene in Parameterform rechnen werden:
Gegeben seien die Gerade $g: X = \left( \begin{array}{c} 1 \\ -3 \\ 2 \end{array} \right) + t \cdot \left( \begin{array}{c} -1 \\ 0 \\ 2 \end{array} \right)$ und die Ebene $\epsilon : X = \left( \begin{array}{c} 4 \\ -1 \\ -3 \end{array} \right) + s \cdot \left( \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right) + u \cdot \left( \begin{array}{c} 2 \\ -1 \\ 0 \end{array} \right)$. Stellen wir nun also unser Gleichungssystem auf:
In der ersten Gleichung drücken wir $u$ in $t$ aus: $u = - \frac{3}{2} - t \cdot \frac{1}{2}$
In der zweiten Gleichung drücken wir $s$ in $u$ aus: $s = -2 + u$
Das $u$ von oben setzen wir nun hier ein und erhalten $s$ in Abhängigkeit von $t$: $s = - \frac{7}{2} - t \cdot \frac{1}{2}$.
Dieses $s$ setzen wir nun in die dritte Gleichung ein und wir erhalten: $2 + 2t = -3 - \frac{7}{2} - t \cdot \frac{1}{2}$ und in weiterer Folge $t = - \frac{17}{5}$.
Es ergibt sich also genau eine Lösung für das Gleichungssystem, was bedeutet, dass die Gerade und die Ebene einen gemeinsamen Schnittpunkt besitzen. Diesen erhalten wir, indem wir den errechneten Wert für $t$ in die Geradengleichung einsetzen (Man könnte natürlich auch noch die Werte für $s$ und $u$ berechnen, und diese in die Ebenengleichung einsetzen; zur Übung kannst du das gerne tun):
$$g: S = \left( \begin{array}{c} 1 \\ -3 \\ 2 \end{array} \right) - \frac{17}{5} \cdot \left( \begin{array}{c} -1 \\ 0 \\ 2 \end{array} \right) = \left( \begin{array}{c} \frac{23}{5} \\ -3 \\ - \frac{24}{5} \end{array} \right)$$
Betrachten wir nun dasselbe Beispiel, mit dem Unterschied, dass die Ebene in Normalform gegeben ist und wir auch gleich mit dieser Form rechnen:
Gegeben seien die Gerade $g: X = \left( \begin{array}{c} 1 \\ -3 \\ 2 \end{array} \right) + t \cdot \left( \begin{array}{c} -1 \\ 0 \\ 2 \end{array} \right)$ und die Ebene $\epsilon : x + 2y - 2z = 8$. Wir setzen die Koordinatengleichungen der Gerade in die Normalform der Ebene ein:
Wenn wir diese Gleichung lösen, erhalten wir wie im ersten Beispiel $t = - \frac{17}{5}$. Dies noch in die Geradengleichung einsetzen und wir erhalten den Schnittpunkt.
Da man bei der zweiten Methode meistens weniger Rechenaufwand hat, zahlt es sich oft aus, die Parameterdarstellung der Ebene in die Normalform ($=$ allg. Ebenengleichung) umzurechnen.
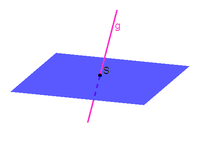
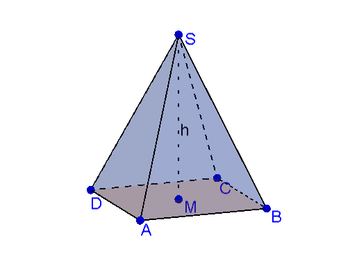
Pyramidenbeispiel
Gegeben seien $3$ Eckpunkte $A(-2 \vert -2 \vert 1), B(2 \vert -2 \vert 1), C(2 \vert 2 \vert 1)$ der quadratischen Grundfläche und die Spitze $S(0 \vert 0 \vert 6)$ einer geraden (gerade bedeutet, dass die Spitze in einem rechten Winkel über dem Mittelpunkt der Grundfläche der Pyramide liegt) Pyramide.Gesucht sind:
- der vierte Eckpunkt $D$ der Grundfläche
- die Parameterdarstellung der Trägergeraden $h$ der Höhe
- die Fläche der Grundfläche
- die Geradengleichung der Geraden $g_{AS}$ auf der $A$ und $S$ liegen in a) Parameterform und b) parameterfreier Form
- Der Winkel $\alpha$ zwischen den Vektoren $\vec{AS}$ und $\vec{AC}$
- Zeige, dass der Schnittpunkt der Geraden $g_{AS}$ und $h$ gleich die Spitze $S$ ist
- Gib die Ebenengleichung $\epsilon$ der Grundfläche in a) Parameterform, b) Normalform und c) allgemeiner Ebenengleichung an
- Berechne den Fußpunkt $M$ der Höhe, indem du $h$ und $\epsilon$ schneidest
1. $D = A + \vec{BC} = \left( \begin{array}{c} -2 \\ -2 \\ 1 \end{array} \right) + \left( \begin{array}{c} 0 \\ 4 \\ 0 \end{array} \right) = \left( \begin{array}{c} -2 \\ 2 \\ 1 \end{array} \right)$
2. $h: X = S + t \cdot \vec{h}$
$$\vec{AB} \times \vec{BC} = \left( \begin{array}{c} 4 \\ 0 \\ 0 \end{array} \right) \times \left( \begin{array}{c} 0 \\ 4 \\ 0 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ 16 \end{array} \right) \ \parallel \ \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) = \vec{h}$$
$$h: X = \left( \begin{array}{c} 0 \\ 0 \\ 6 \end{array} \right) + t \cdot \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right)$$
3. $G = \parallel \vec{AB} \times \vec{BC} \parallel = \parallel \left( \begin{array}{c} 0 \\ 0 \\ 16 \end{array} \right) \parallel = 16FE$
4. a) $g_{AS}: X = A + u \cdot \vec{AS}$
$$\vec{AS} = \left( \begin{array}{c} 2 \\ 2 \\ 5 \end{array} \right) \ \Rightarrow \ g_{AS}: X = \left( \begin{array}{c} -2 \\ -2 \\ 1 \end{array} \right) + u \cdot \left( \begin{array}{c} 2 \\ 2 \\ 5 \end{array} \right)$$ oder $$g_{AS}:\begin{cases} x = -2 + 2u \\ y = -2 + 2u \\ z = 1 + 5u \end{cases}$$
b) Parameter elimieren:
$$x - y: x-y = 0$$
$$5x - 2z: 5x - 2z = -12$$
$$\Rightarrow g_{AS}:\begin{cases} x - y = 0 \\ 5x - 2z = -12 \end{cases}$$
5. $\measuredangle \vec{AS},\vec{AC} = \alpha = arccos{\frac{\vec{AS} \cdot \vec{AC}}{\parallel \vec{AS} \parallel \cdot \parallel \vec{AC} \parallel}} = arccos{\frac{\left( \begin{array}{c} 2 \\ 2 \\ 5 \end{array} \right) \cdot \left( \begin{array}{c} 4 \\ 4 \\ 0 \end{array} \right)}{\parallel \left( \begin{array}{c} 2 \\ 2 \\ 5 \end{array} \right) \parallel \cdot \parallel \left( \begin{array}{c} 4 \\ 4 \\ 0 \end{array} \right) \parallel}} = arccos{\frac{16}{\sqrt{33 \cdot 32}}} = 60,5°$
6. $g_{AS}$ und $h$ gleichsetzen:
$$\begin{align}
I: \ &-2&+&2u&=&0&& \\
II: \ &-2&+&2u&=&0&& \\
III: \ & \ \ 1&+&5u&=&6&+&t
\end{align}
\ \ \ \rightarrow u=1$$
$$g_{AS}: S = \left( \begin{array}{c} -2 \\ -2 \\ 1 \end{array} \right) + 1 \cdot \left( \begin{array}{c} 2 \\ 2 \\ 5 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ 6 \end{array} \right)$$
7. a) $\epsilon: X = A + v \cdot \vec{AB} + w \cdot \vec{BC} \ \rightarrow \ \epsilon: X = \left( \begin{array}{c} -2 \\ -2 \\ 1 \end{array} \right) + v \cdot \left( \begin{array}{c} 4 \\ 0 \\ 0 \end{array} \right) + w \cdot \left( \begin{array}{c} 0 \\ 4 \\ 0 \end{array} \right)$
b) $\epsilon: \vec{n} \cdot \vec{X} = \vec{n} \cdot \vec{A} \ \rightarrow \ \epsilon: \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \cdot \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \cdot \left( \begin{array}{c} -2 \\ -2 \\ 1 \end{array} \right)$
c) $\epsilon: z = 1$
8. $h:\begin{cases} x=0 \\ y=0 \\ z=6+t \end{cases} \ \ \epsilon: z=1 \ \ \rightarrow \ 1 = 6 + t \ \Rightarrow \ t=-5$
$h: M = \left( \begin{array}{c} 0 \\ 0 \\ 6 \end{array} \right) -5 \cdot \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right)$
Inhaltsverzeichnis
Interaktive Übungen
Quiz: Grundlagen und geometrische Deutung von Vektoren und Rechenoperationen (AG 3.1-3.3)
Quiz: Vektoren - Geraden in der Ebene (AG 3.4)
Quiz: Vektoren - Geraden im Raum (AG 3.4)
Quiz: Normalvektoren (AG 3.5)
Weitere Aufgaben
Grundlagen der Vektorrechnung
VektorrechnungGLBspAngabe.pdf
VektorrechnungGLBspLösung.pdf
Vektorrechnung im $\mathbb{R^2}$
VektorrechnungR2BspAngabe.pdf
VektorrechnungR2BspLösung.pdf