Matrizen
Die Matrizenrechnung ist ein nützliches Werkzeug, um ein Gleichungssystem mit vielen linearen Gleichungen zu lösen oder auch um Tabellen übersichtlich darzustellen, also um lineare Zusammenhänge zwischen mehreren Größen herzustellen.
- Einführung
- Rechenregeln
- Gozinto-Graphen
- Input-Output-Matrix: Leontief-Modell
- Saklierungsmatrix
- Drehung
- homogene Koordinaten
- Schiebung
- Spiegelung
- Matura-Aufgaben
Einführung
Will man ein lineares Gleichungssystem lösen, kann das mit den bereits bekannten Verfahren wie Additions-, Gleichsetzungs- oder dem Substitutionsverfahren geschehen, doch wird das bei einem großen Gleichungssystem schnell unübersichtlich und mühsam. Daher wird eine neue Schreibweise eingeführt.
Das Gleichungssytem \begin{align} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 &= y_1 \\ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 &= y_2 \\ \end{align} bei dem $x_1 , x_2, x_3$ gesucht sind, kann auch in Matrixschreibweise geschrieben werden: $$\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21}&a_{22}&a_{23}\\ \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \end{pmatrix},$$
wobei die Matrizenmultiplikation weiter unten erklärt wird. Man nennt
$$ \begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ \end{pmatrix} $$ eine $2\times3$ Matrix, sie besteht aus 2 Zeilen und 3 Spalten, $\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$ nennt man eine $3 \times 1$ Matrix und $\begin{pmatrix} y_1 \\ y_2 \end{pmatrix}$ eine $2 \times 1$ Matrix. Der erste Index gibt dabei an in der welcher Zeile und der zweite Index in welcher Spalte sich die Zahl befindet. Hier bilden zum Beispiel $a_{11}$, $ a_{12}$ und $ a_{13}$ die erste Zeile, $a_{21}$, $ a_{22}$ und $ a_{23} $ die zweite Zeile. $a_{11}$ und $ a_{21}$ bilden die erste Spalte, $a_{12}$ und $a_{22}$ die zweite Spalte und $ a_{13}$ und $ a_{23}$ und die dritte Spalte
Mit $A:=\begin{pmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
\end{pmatrix}$ , $\vec{x} =\begin{pmatrix}
x_1 \\ x_2 \\ x_3
\end{pmatrix}$ und $\vec{y}=\begin{pmatrix}
y_1 \\ y_2
\end{pmatrix}$ kann man das Gleichungssystem sehr kompakt als
$A \cdot \vec{x}= \vec{y}$ schreiben. Das Lösen des Gleichungssystems erfolgt dann über Äquivalenzumformen von $(A|\vec{y})$, d.h. der Matrix
$$\left( \begin{array}{ccc}
a_{11} & a_{12} &a_{13}\\
a_{21} & a_{22} &a_{23}\\
\end{array} \right| \left. \begin{array}{c} y_1 \\y_2 \end{array}\right)$$
Beispiel: $a_{11}=3 \qquad a_{12}=6 \qquad a_{13}=2 \qquad a_{21}=7 \qquad a_{22}=8 \qquad a_{23}=1$
$$ A= \begin{pmatrix} 3 & 6 &2\\7 & 8 &1\\ \end{pmatrix} $$
Gib die erste Zeile der Matrix $\quad F= \begin{pmatrix}
8 & 12 &17 \\
3,9 & 5 & 84,7 \\
4,5 &63 & 9,6\\
\end{pmatrix} $ und die 3. Spalte der Matrix $F$ an!
3.Spalte $\left(\begin{array}{c} 17 \\ 84,7 \\ 9,6 \end{array}\right)$
|
$m \times n$ Matrix
$ \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} &\dots & a_{2n} \\ \vdots & \vdots &\ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{pmatrix} \quad \in \mathbb{R}^{m \times n} \qquad \forall m,n \in \mathbb{N} $ Die $m\times n$ Matrix hat $m$ Zeilen und $n$ Spalten. |
|
Eine quadratische Matrix hat die gleiche Anzahl an Zeilen und Spalten, also $m=n$. Damit ein Gleichungssystem eine eindeutige Lösung haben kann, muss die Matrix $A$ quadratisch sein, das heißt gleich viele Gleichungen wie Unbekannte haben. |
|
Nullmatrix
Die Nullmatrix $0_n$ ist wie folgt definiert: $ 0= \begin{pmatrix} 0 & \dots & 0 \\ \vdots & & \vdots \\ 0 & \dots & 0 \\ \end{pmatrix} \quad \in \mathbb{R}^{n \times n} \qquad \forall n \in \mathbb{N} $ Es gilt $A + 0 =0+A =A$ und $ A \cdot 0 = 0 \cdot A=0$. |
|
Einheitsmatrix
Die Einheitsmatrix $I_n$ hat nur in der Hauptdiagonale (von links oben nach rechts unten) Einsen stehen. Sonst befinden sich überall Nullen. Zudem ist sie eine quadratische Matrix. $ I_n= \begin{pmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 &0 & \dots & 1 \\ \end{pmatrix} \quad \in \mathbb{R}^{n \times n} \qquad \forall n \in \mathbb{N} $ Die Einheitsmatrix wird benötigt, um ein lineares Gleichungssystem in Matrixform zu lösen und um die Inverse einer Matrix zu definieren, also $A \dot I= A$. Ist $B$ die Inverse zu $A$, dann $ A\cdot B = I =B \cdot A$. |
Gib die Einheitsmatrix im dreidimensionalen Raum an!
Rechenregeln
|
Bei der Addition von Matrizen, werden die gleichen Komponenten miteinander addiert.
dann ist $A +B = \begin{pmatrix} a_{11} + b_{11} & a_{12}+ b_{12} + & \dots +& a_{1n} + b_{1n} \\ a_{21} + b_{21} & a_{22} + b_{22} + &\dots +& a_{1n}+ b_{2n} \\ \vdots & \vdots &\ddots & \vdots \\ a_{m1}+ b_{m1} &a_{m2} + b_{m2} & + \dots +& a_{mn} + b_{mn} \end{pmatrix} $ Bei der Addition müssen beide Matrizen dieselbe Dimension haben, das heißt dieselbe Anzahl von Zeilen und Spalten. |
Bei der $2\times 2$ Matrix schaut das wie folgt aus
$ A= \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{pmatrix} $
$ B= \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{pmatrix} $
dann ist $ \qquad \qquad \qquad A+ B =\begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} = \begin{pmatrix} a_{11} + b_{11} & a_{12} + b_{12} \\ a_{21} + b_{21} & a_{22} + b_{22} \\ \end{pmatrix}$
Addiere die Matrizen $\quad C= \begin{pmatrix}
8 & 6 \\
0 & -4 \\
\end{pmatrix} \quad $ und
$\quad D= \begin{pmatrix}
2 & -1 \\
5 & 3 \\
\end{pmatrix}$.
In der Firma $A$ wird 8 mal das Produkt 1 hergestellt, 5 mal Produkt 2, 12 mal Produkt 3 und 7 mal Produkt 4, in der Firma Firma $B$ wird 2 mal das Produkt 1 hergestellt, 1 mal Produkt 2, 3 mal Produkt 3 und 9 mal Produkt 4,
Firma $C$ wird 0 mal das Produkt 1 hergestellt, 17 mal Produkt 2, 3 mal Produkt 3 und 9 mal Produkt 4,
Firma $D$ wird 3 mal das Produkt 1 hergestellt, 4 mal Produkt 2, 2 mal Produkt 3 und 5 mal Produkt 4.
Wie viel wird insgesamt von den jeweiligen Produkten hergestellt?
Addiere die beiden Matrizen und füge die Zahlen der Lösungsmatrix in die Zellen ein, dann klicke auf überprüfen.
Subtrahiere die beiden Matrizen und füge die Zahlen der Lösungsmatrix in die Zellen ein, dann klicke auf überprüfen.
|
Bei der Multiplikation mit einem Skalar $k$ (einer reellen Zahl), wird jede Komponente einzeln mit dem Skalar multipliziert.
$ k \cdot A= \begin{pmatrix} k \cdot a_{11} & k \cdot a_{12} & \dots & k \cdot a_{1n} \\ k \cdot a_{21} & k \cdot a_{22} & \dots & k \cdot a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ k \cdot a_{m1} &k \cdot a_{m2} & \dots & k \cdot a_{mn} \\ \end{pmatrix} $ |
Multipliziere die Matrix $\quad E= \begin{pmatrix}
7 & 2 \\
9 & 0 \\
\end{pmatrix} \quad $ mit $3$.
Multipliziere die Matrix mit dem Skalar und füge die Zahlen der Lösungsmatrix in die Zellen ein, dann klicke auf überprüfen.
|
Transponierte Matrix
Bei einer transponierten Matrix werden die Zeilen und Spalten miteinander vertauscht. Sei $A$ die ursprüngliche Matrix und $A^T$ die transponierte Matrix: $A= \begin{pmatrix} a_{11} & a_{12} &a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} &a_{32} & a_{33} \\ \end{pmatrix} $ dann ist $A^T= \begin{pmatrix} a_{11} & a_{21} &a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} &a_{23} & a_{33} \\ \end{pmatrix} $ |
Gib die transponierten Matrizen zu den Matrizen $B$ und $C$ an!
$\quad B= \begin{pmatrix}
9 & 4 \\
654 & 274 \\
\end{pmatrix} $
$\quad C= \begin{pmatrix}
65 & 4,7 &6 &9 &89 \\
8,3 & 2,4 & 7 & 3&1 \\
4 & 2 & 0 & 7,9 & 5\\
\end{pmatrix} $
|
Matrizenmultiplikation
Zwei Matrizen werden nach der Regel: Zeile mal Spalte multipliziert. Die Matrizenmultiplikation ist nicht kommutativ, das heißt: $A\cdot B \neq B \cdot A$. Um $A \cdot B =C$ zu erhalten muss die Anzahl der Spalten von $A$ die selbe sein wie die Anzahl der Zeilen von $B$. Also wenn $A$ eine $m \times n$ Matrix ist und $B$ eine $n \times p$ Matrix, so sind $m$ und $p$ beliebig und $n$ muss bei $A$ und $B$ dieselbe Zahl sein. Außerdem ist dann $C$ eine $m \times p$ Matrix, sie hat also dieselbe Anzahl der Zeilen wie die Matrix $A$ und dieselbe Spaltenanzahl wie die Matrix $B$. |
Sei die Matrix $A$ zum Beispiel eine $2 \times 3$ Matrix und $B$ eine $3 \times 4$ Matrix. Dann ist die Matrix $A \cdot B = C$ eine $2 \times 4$ Matrix.
Wie erhält man nun die einzelnen Koeffizienten der Matrix $C$?
\url{https://www.youtube.com/watch?v=iLgfkgscafQ}
Die Durchführung der Matrizenmultiplikation kann mit Hilfe der Falk'schen Anordnung erfolgen:
| $ \begin{pmatrix} 8 &1 & 3 \\9 & 0 & 5 \\ \end{pmatrix} $ | |
| $ \begin{pmatrix} 2 & 5 \\4 & 7 \\ \end{pmatrix} $ | $ \begin{pmatrix} c_{11} & c_{12} & c_{13}\\ c_{21} & c_{22} & c_{23} \\ \end{pmatrix} $ |
Wobei $$c_{11} = 2 \cdot 8 + 5 \cdot 9 = 61\\ c_{12} = 2 \cdot 1 + 5 \cdot 0 =2\\ c_{13} = 2 \cdot 3 + 5 \cdot 5 =31\\ c_{21} = 4 \cdot 8 + 7 \cdot 9 =95\\ c_{22} = 4 \cdot 1 + 7 \cdot 0 =4\\ c_{23}= 4 \cdot 3 + 7 \cdot 5 =47$$ Also $$\begin{pmatrix} 2 & 5 \\ 4 & 7 \\ \end{pmatrix} \cdot \begin{pmatrix} 8 &1 & 3 \\ 9 & 0 & 5 \\ \end{pmatrix} = \begin{pmatrix} 61 & 2 & 31\\ 95 & 4 & 47 \\ \end{pmatrix} $$
Berechne $A \cdot B =
\begin{pmatrix}
5 & 7 & 1 \\
8 & -1 & 4 \\
\end{pmatrix} \cdot
\begin{pmatrix}
9 & 7 \\
3 & -6 \\
0 & 2 \\
\end{pmatrix}
$
Multipliziere die beiden Matrizen und füge die Zahlen der Lösungsmatrix in die Zellen ein, dann klicke auf überprüfen.
Gozinto-Graphen
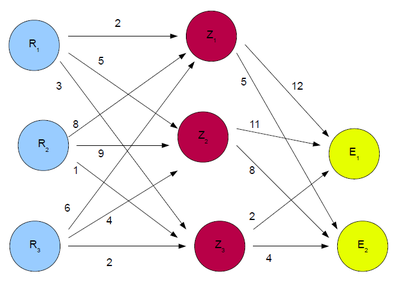
Gonzinto-Graphen dienen der Veranschaulichung der Zusammenhänge zwischen Roh-, Zwischen- und Endprodukten. Die Knoten stellen dabei die Teile dar und die Pfeile oder auch gerichtete Kanten die Mengenbeziehungen.
In der Abbildung des Gozintographen wird der Zusammenhang zwischen den Rohstoffen $R_1 , R_2$ und $R_3$ mit den Zwischenprodukten $Z_1, Z_2, Z_3$ und den Endprodukten $E_1, E_2$ dargestellt.
In einer Tabelle kann der Zusammenhang wie folgt aufgelistet werden:
| $Z_1$ | $Z_2$ | $Z_3$ | |
|---|---|---|---|
| $R_1$ | 2 | 5 | 3 |
| $R_2$ | 8 | 9 | 1 |
| $R_3$ | 6 | 4 | 2 |
| $E_1$ | $E_2$ | |
|---|---|---|
| $Z_1$ | 12 | 5 |
| $Z_2$ | 11 | 8 |
| $Z_3$ | 2 | 4 |
Die Tabelle kann aber ebenso in Matrixform umgeschrieben werden, wobei die Matrix $RZ$ den Zusammenhang der Rohstoffe mit den Zwischenprodukten und $ZE$ den der Zwischenprodukte mit den Endprodukten beschreibt.
$$ RZ= \begin{pmatrix} 2 & 5 & 3 \\8 & 9 &1 \\ 6&4&2\\ \end{pmatrix} $$ $$ ZE=\begin{pmatrix} 12 & 5 \\ 11 & 8 \\ 2&4\\ \end{pmatrix} $$
Um eine Matrix zu erhalten, welche den Rohstoffbedarf für die Endprodukte beschreibt wird die Matrix $RZ$ mit der Matrix $ZE$ multipliziert. In unserem Beispiel ergibt das
\begin{equation*} RE= RZ \cdot ZE= \begin{pmatrix} 24 +55+ 6 & 10 +40+ 12\\ 96 +99 +2 & 40+ 72+ 4\\ 72 +44+ 4 & 30+ 32+ 8\\ \end{pmatrix} = \begin{pmatrix} 85 &62\\ 197 & 116\\ 120 & 70\\ \end{pmatrix}. \end{equation*}
Die Matrizen $RZ$, $ZE$ und $RE$ werden auch Produktionsmatrix genannt. Der Produktions-, Output- oder Nachfragevektor gibt an wie viel der Endprodukte produziert werden sollen. Der Bedarfsvektor gibt den Gesamtbedarf an Einzelteilen an für einen vorgesehenen Produktionsvektor. Also durch den Bedarfsvektor kann der Bedarf an Rohstoffen berechnet werden.
Im Preisvektor befinden sich die Preise für die einzelnen Rohstoffe. Der Inputvekor beschreibt die benötigten Rohstoffe.
Input-Output-Matrix: Leontief-Modell
Eine Input-Output-Tabelle für die Firmen A, B und C, mit $x_i=\sum_{k=1}^{3} x_{ik} y_i$, wobei $i=j$ den Eigenbedarf einer Firma beschreibt, wird in der folgenden Tabelle aufgezeigt.
| Input / Output | A | B | C | Markt / Konsum | Gesamtproduktion |
|---|---|---|---|---|---|
| A | $x_{11}$ | $x_{12}$ | $x_{13}$ | $y_{1}$ | $x_{1}$ |
| B | $x_{21}$ | $x_{22}$ | $x_{23}$ | $y_{2}$ | $x_{2}$ |
| C | $x_{31}$ | $x_{32}$ | $x_{33}$ | $y_{3}$ | $x_{3}$ |
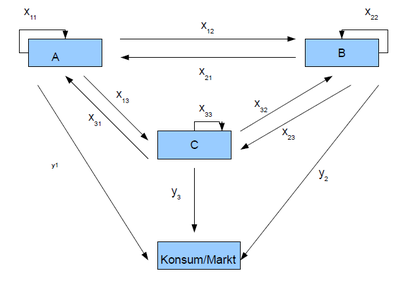
In einem Gozinto-Graphen kann dies, wie rechts unten zu sehen ist, dargestellt werden:
Die Produktionsmatrix $P$ sieht daher folgendermaßen aus:
$P=\begin{pmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\x_{31} & x_{32} & x_{33}\\ \end{pmatrix}.$
Um die Input-Output-Matrix zu erhalten die erste Spalte durch den Wert der Gesamtproduktion der ersten Zeile geteilt werden, die zweite Spalte durch den der zweiten Zeile und die dritte Spalte durch den der dritten Zeile, das heißt die Koeffizienten der Input-Output-Matrix ergeben sich als $a_{ij}= \frac{x_{ij}}{x_j}$
Die Input-Output-Matrix ergibt sich dann zu: $M=\begin{pmatrix} \frac{x_{11}}{x_1} & \frac{x_{12}}{x_2} & \frac{x_{13}}{x_3} \\ \frac{x_{21}}{x_1} & \frac{x_{22}}{x_2} & \frac{x_{23}}{x_3} \\ \frac{x_{31}}{x_1} & \frac{x_{32}}{x_2} & \frac{x_{33}}{x_3}\\ \end{pmatrix}.$
Gib die Input-Output-Matrix zu folgendem Gozintographen an:
Datei:beispiel inpuoutput.pdf
Dieser und die folgenden Abschnitte sind nur für HTL-SchhülerInnen relevant.
Saklierungsmatrix
Um einen Vektor zu stauchen oder zu strecken, wird er mit einem Faktor multipliziert.
\begin{align*} x'&=x \cdot s_x\\ y'&=y\cdot s_y \\ z' &= z \cdot s_z \end{align*} In Matrixform kann er mit der Skalierungsmatrix multipliziert werden.
$$U=\begin{pmatrix}s_x & 0 & 0\\ 0 & s_y & 0 \\ 0& 0 &s_z \\ \end{pmatrix} $$ Dabei gibt $s_x$ die Skalierung in x-Richtung, $s_y$ die Skalierung in y-Richtung und $s_z$ die Skalierung in z-Richtung an.
Drehung
Die Drehung ist ein Beispiel für die Anwendung und Motivation der Matrizenmultiplikation. In $\mathbb{R}^2$ und $\alpha \in [0, 2 \pi[$ wird die Drehung (gegen den Uhrzeigersinn) eines Vektors $v$ um den Winkel $\alpha $ durch die Multiplikation des Vektors mit der Drehmatrix $$R_{\alpha} \begin{pmatrix} \cos(\alpha) & -\sin(\alpha) \\\sin(\alpha) & \cos(\alpha) \\ \end{pmatrix} $$ erreicht: $v'=R_\alpha \cdot v$.
In $\mathbb{R}^3$ ergeben sich für die Drehungen um die
- x-Achse:
$$R_x(\alpha)=\begin{pmatrix}1&0 & 0\\ 0& \cos(\alpha) & -\sin(\alpha) \\ 0& \sin(\alpha) & \cos(\alpha) \\ \end{pmatrix} $$
- y-Achse:
$$R_y(\alpha)=\begin{pmatrix}\cos(\alpha) &0 & \sin(\alpha) \\ 0& 1 & 0 \\ - \sin(\alpha)& 0 & \cos(\alpha) \\ \end{pmatrix} $$
- z-Achse
$$R_z(\alpha)=\begin{pmatrix}\cos(\alpha) & -\sin(\alpha) & 0\\
\sin(\alpha) & \cos(\alpha) & 0 \\
0& 0 & 1 \\
\end{pmatrix}
$$
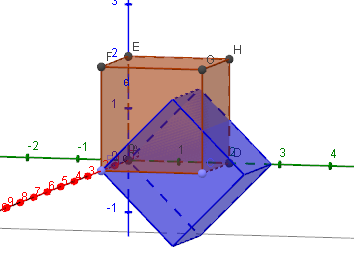
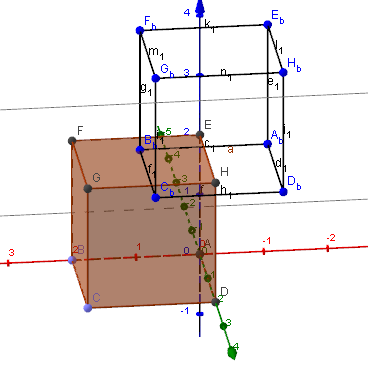
Welche Koordinaten erhältst du , wenn der Würfel mit den Eckpunkten
\begin{align*}
A=\begin{pmatrix}
0\\ 0\\ 0\\
\end{pmatrix}, & &
B=\begin{pmatrix}
2\\ 0 \\ 0\\
\end{pmatrix}, & &
C=\begin{pmatrix}
2\\ 2 \\ 0\\
\end{pmatrix}, & &
D=\begin{pmatrix}
0 \\ 2 \\ 0\\
\end{pmatrix}, \\
E=\begin{pmatrix}
0 \\ 0 \\2 \\
\end{pmatrix}, & &
F=\begin{pmatrix}
2 \\ 0 \\2 \\
\end{pmatrix}, & &
G=\begin{pmatrix}
2 \\ 2\\ 2\\
\end{pmatrix}, & &
H=\begin{pmatrix}
0 \\2 \\2\\
\end{pmatrix}
\end{align*}
um die x-Achse um den Winkel $\alpha= 45^{\circ}$ gedreht wird?
$R_x(45^{\circ}) =\begin{pmatrix} 1 & 0 & 0 \\ 0& \cos5^{\circ}) & -\sin(45^{\circ}) \\ 0 & \sin(45^{\circ}) & \cos(45^{\circ}) \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2} } & -\frac{1}{\sqrt{2} } \\ 0 & \frac{1}{\sqrt{2} } & \frac{1}{\sqrt{2} } \\ \end{pmatrix}$ ergeben sich die Punkte des gedrehten Würfels durch die Muliplikation des ursprünglichen Punktes mit der Rotationsmatrix \begin{align*} A_x= A\cdot R_x(45^{\circ}) = \begin{pmatrix} 0\\ 0\\ 0\\ \end{pmatrix}, & & B_x=\begin{pmatrix} 2\\ 0 \\ 0\\ \end{pmatrix}, & & C_x=\begin{pmatrix} 2\\ \sqrt{2} \\ \sqrt{2} \\ \end{pmatrix}, & & D_x=\begin{pmatrix} 0 \\ \sqrt{2} \\ \sqrt{2}\\ \end{pmatrix}, \\ E_x=\begin{pmatrix} 0 \\ -\sqrt{2} \\\sqrt{2} \\ \end{pmatrix}, & & F_x=\begin{pmatrix} 2 \\ -\sqrt{2} \\\sqrt{2} \\ \end{pmatrix}, & & G_x=\begin{pmatrix} 2 \\ 0\\ 2\sqrt{2}\\ \end{pmatrix}, & & H_x=\begin{pmatrix} 0 \\0 \\2\sqrt{2}\\ \end{pmatrix}. \end{align*}
homogene Koordinaten
Homogene Koordinaten werden zum Beispiel verwendet wenn eine Verschiebung eines Vektors durchgeführt werden soll, also wenn eine nicht lineare Transformation stattfindet.
Euklidische Koordinaten in $\mathbb{R}^3$ werden wie folgt in homogenen Koordinaten umgeschrieben $$\begin{pmatrix} x\\ y\\ z \end{pmatrix} \mapsto \begin{bmatrix} x \\ y\\ z\\1 \end{bmatrix} .$$
Schiebung
Die Schiebung eines Vektors $\begin{pmatrix} x\\ y\\ \end{pmatrix}$ um den Vektor $\begin{pmatrix} t_x \\ t_y \\ \end{pmatrix}$ ist nicht linear und deshalb müssen die Koordinaten in homogenen Koordinaten geschrieben werden, damit man die Schiebung in Matrixform schreiben kann.
So erhält man für die Translation:
\begin{align*} x'&=x + t_z \\ y'&= y +t_y \\ \end{align*} $\Rightarrow$
\begin{equation*} \begin{pmatrix} x'\\ y' \\ 1\\ \end{pmatrix} =\begin{pmatrix} 1 &0&t_x\\ 0&1& t_y\\ 0&0&1\\ \end{pmatrix} \cdot\begin{pmatrix} x\\ y\\1\\ \end{pmatrix}. \end{equation*}
Im $\mathbb{R}^3$ ergibt sich für die Schiebung
\begin{equation*} T_3=\begin{pmatrix} 1&0 &0&t_x \\ 0& 1 &0&t_y \\ 0&0&1& t_z \\ 0&0&0&1 \end{pmatrix} \end{equation*}
Spiegelung
Die Spiegelung ist ein Sonderfall der Skalierung mit entweder $s_x=-1$, $s_y=-1$ oder $s_z=-1$, je nachdem um welche Achse gespiegelt werden soll, die anderen Skalierungsfaktoren sollen dabei den Wert $1$ annehmen.
Es ergeben sich also die verschiedenen Spiegelungsmatrizen, je nach Spiegelungsachse:
im $\mathbb{R}^2$:
- um die x-Achse:
$S_x=\begin{pmatrix} 1&0 \\ 0& -1 \\ \end{pmatrix}$
- um die y-Achse:
$S_y=\begin{pmatrix}-1&0 \\ 0& 1 \\ \end{pmatrix}$
-im $\mathbb{R}^3$
- um die yz-Ebene:
\begin{equation*} S_{yz}= \begin{pmatrix} -1&0 &0\\0& 1 &0\\ 0&0&1 \end{pmatrix} \end{equation*}
- um die xz-Ebene:
\begin{equation*} S_{xz}= \begin{pmatrix} 1&0 &0\\0& -1 &0\\ 0&0&1 \end{pmatrix} \end{equation*}
- um die xy-Ebene:
\begin{equation*} S_{xy}= \begin{pmatrix} 1&0 &0\\0& 1 &0\\ 0&0&-1 \end{pmatrix} \end{equation*}
Spiegelung an einer Geraden
Die Spiegelung eines Punktes im $\mathbb{R}^2$ an einer Gerade $g: y=ax+b$ erfolgt in homogenen Koordinaten in den folgenden fünf Schritten:
1.) Das Koordinatensystem so verschieben, dass die Spiegelungsachse durch den Koordinatenursprung geht.
2.) Die Spiegelungsachse soll um den Winkel $\arctan(a)$ gedreht werden, so dass sie mit der x-Achse zusammenfällt.
3.) Spieglung an der x-Achse.
4.) In Ausgangsposition zurückdrehen, also Schritt 2) in die andere Richtung.
5.) Die Spiegelungsachse zurück schieben, also wie in Schritt 1), nur in die andere Richtung schieben.
Damit die Matrizen alle miteinander multipliziert werden können, müssen sie in den selben Koordinaten geschrieben werden, da eine Translation angewendet wird, sollten alle Matrizen in homogenen Koordinaten angeschrieben werden.
Für die jeweiligen Schritte gibt es eine passende Matrix, werden die fünf Matrizen miteinander multipliziert erhält man die Spiegelungsmatrix um die Gerade $g$, mit $arctan(a):=t$.
$$ \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & b \\ 0& 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} \cos\left(t\right) & -\sin\left(t\right) & 0\\ \sin\left(t\right) & \cos\left(t\right) & 0 \\ 0& 0 & 1 \\ \end{pmatrix} \cdot\begin{pmatrix} 1 & 0 & 0\\ 0 & -1 & 0 \\ 0& 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} \cos\left(-t\right) & -\sin\left(-t\right) & 0\\ \sin\left(-t\right) & \cos\left(-t\right) & 0 \\ 0& 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & -b \\ 0& 0 & 1 \\ \end{pmatrix} $$